基于应变梯度理论的微尺度蜂窝等效模量计算方法
贺 丹, 刘圣乔, 冯佳月
(沈阳航空航天大学 辽宁省飞行器复合材料结构分析与仿真重点实验室,沈阳 110136)
1 引 言
蜂窝结构因其优良的力学性能广泛应用于航空航天、交通运输及建筑等领域[1]。因为蜂窝的结构较为复杂,所以在设计和计算过程中通常将其等效为均质材料,而等效方法的准确性则直接影响着蜂窝夹层结构的设计质量和使用安全。
Allen[2]最早开展了蜂窝面内等效模量的计算方法研究,采用反平面假设,在计算过程中仅考虑了横向剪切刚度而忽略了芯层的面内刚度和弯曲刚度。Gibson等[3]将胞壁的变形简化为欧拉梁的弯曲问题,计算了芯层面内等效剪切模量,并通过试验验证了该方法的准确性。富明慧等[4]考虑了胞壁伸缩变形的影响,对Gibson的等效模量公式进行了修正。赵金森[5]则在富明慧的基础上,进一步明确了等壁厚蜂窝面内等效模量的计算方法。
随着需求的增长与工艺的进步,蜂窝结构的尺寸有逐步发展到微纳米级别的趋势,因此有必要将尺寸效应[6]纳入到蜂窝等效模量的计算过程当中。尺寸效应主要表现为本构关系会受结构几何尺寸的影响,传统连续介质力学理论无法解释这种现象,因此发展了一些广义连续介质力学理论来唯象地描述尺寸效应的影响。这些理论都需要在本构方程中引入额外的材料尺度参数,且不同的理论需要的材料尺度参数的个数和定义都不尽相同[7]。这些参数的确定是较为困难的,为了便于工程应用,学者们持续努力地发展需要较少尺度参数的新理论。Yang等[8]提出了仅含有一个尺度参数的适用于各向同性材料的修正偶应力理论。陈万吉等[9]将其推广到了各向异性材料。基于修正偶应力理论,张春浩等[10]研究了微纳米蜂窝的等效模量的计算方法。Mindlin[11]提出了应变梯度理论,认为连续介质中的胞元除了宏观运动与变形外,还存在微观位移和变形,因此应考虑应变梯度的影响。其重写的中心对称的各向同性物体的变形方程中包含五个尺度参数[12]。Lam等[13]在Mindlin方程中引入了力偶矩平衡关系,由此重建了应变梯度理论,将尺度参数从五个减少到三个。Aifantis等[14]简化了Mindlin应变梯度理论,将五个尺度参数简化为一个,非常便于工程应用。近年,众多学者[15,16]仍针对应变梯度理论进行改进与应用,其中Shahriari等[17]应用Aifantis简化的应变梯度理论计算了碳纳米管增强复合材料的自由振动。
综上所述,将尺寸效应纳入到蜂窝的等效模量计算中非常必要,但相关的研究工作较少,尤其是基于应变梯度理论的工作还尚未见诸报道。本文从Aifantis的单尺度参数应变梯度理论出发,发展能够计及尺寸效应的微纳米蜂窝面内等效模量的计算方法,并与宏观等效理论的结果进行了对比,讨论了尺寸效应对蜂窝力学性能的影响。
2 Y型蜂窝胞元
蜂窝结构是规律重复的几何结构,对蜂窝分块有利于分析。如图1(a)所示,用矩形虚线分割蜂窝,得到的Y型蜂窝胞元可使面积不变,并且胞元含有的完整胞壁数不变。蜂窝各部分参数如图1(b)所示,其中,L表示角度为θ的胞壁长度,h表示竖直方向胞壁长度,t为胞壁厚度,b为蜂窝高度。
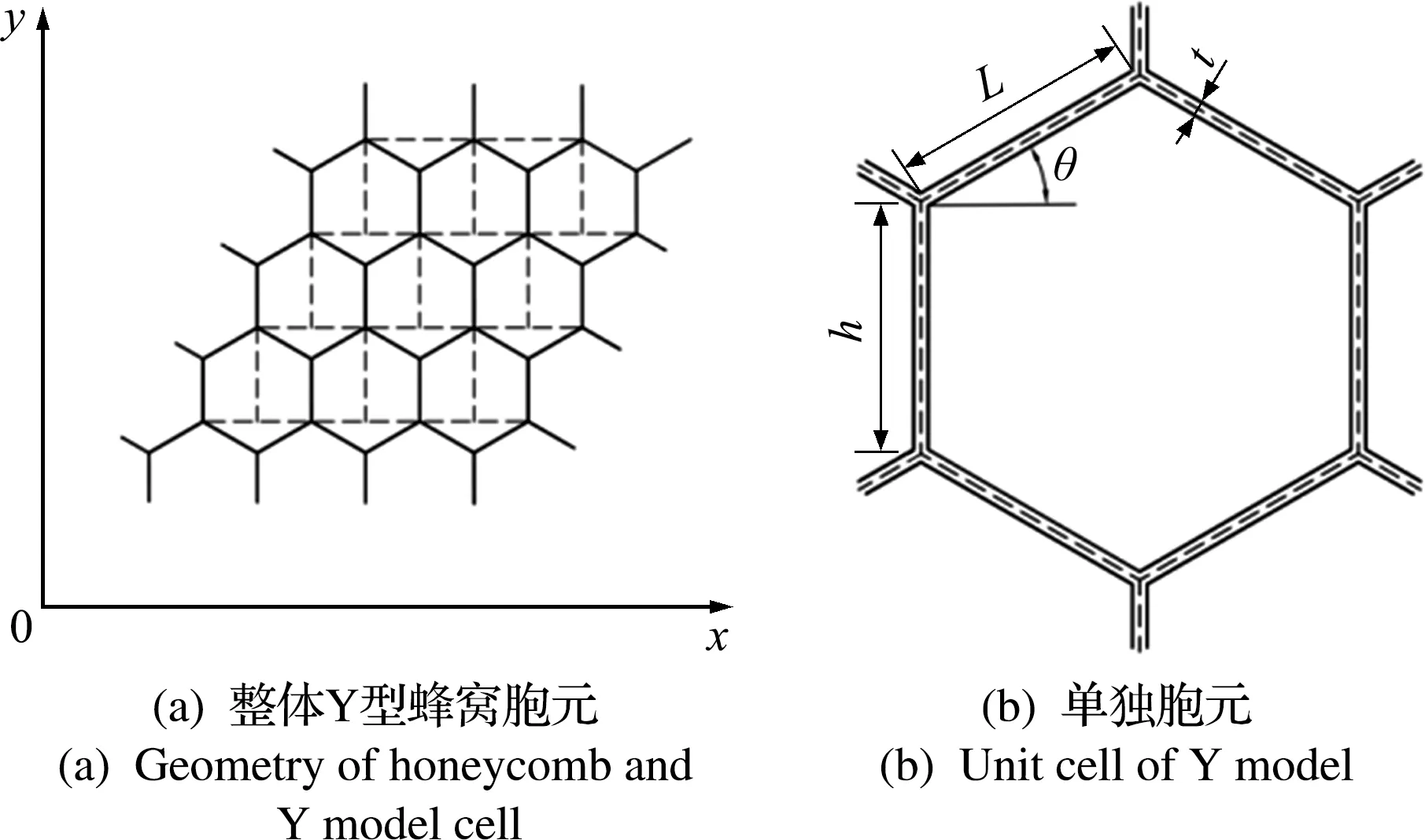
图1 Y型蜂窝胞元
3 应变梯度理论
根据Aifantis[14]提出的应变梯度理论,蜂窝材料的本构方程可表示为
σi j=Ci j k l(1-l22)εk l
(1)
式中l为尺度参数,σi j,εk l,Ci jkl和2分别为应力张量分量、应变张量分量、弹性张量分量和拉普拉斯算子。
应变张量分量εi j的表达式为
(2)
式中ui,j为位移的一阶偏导数。体积为V的线弹性体发生小变形时的应变能可表示为
(i,j=1,2,3)
(3)
4 等效模量的求解
可将蜂窝胞壁简化为在自由端受横向剪切力F、轴向力N和力矩M的悬臂梁,如图2所示。计算胞元的应变能,然后根据能量等效原理,得出等效的面内弹性模量。
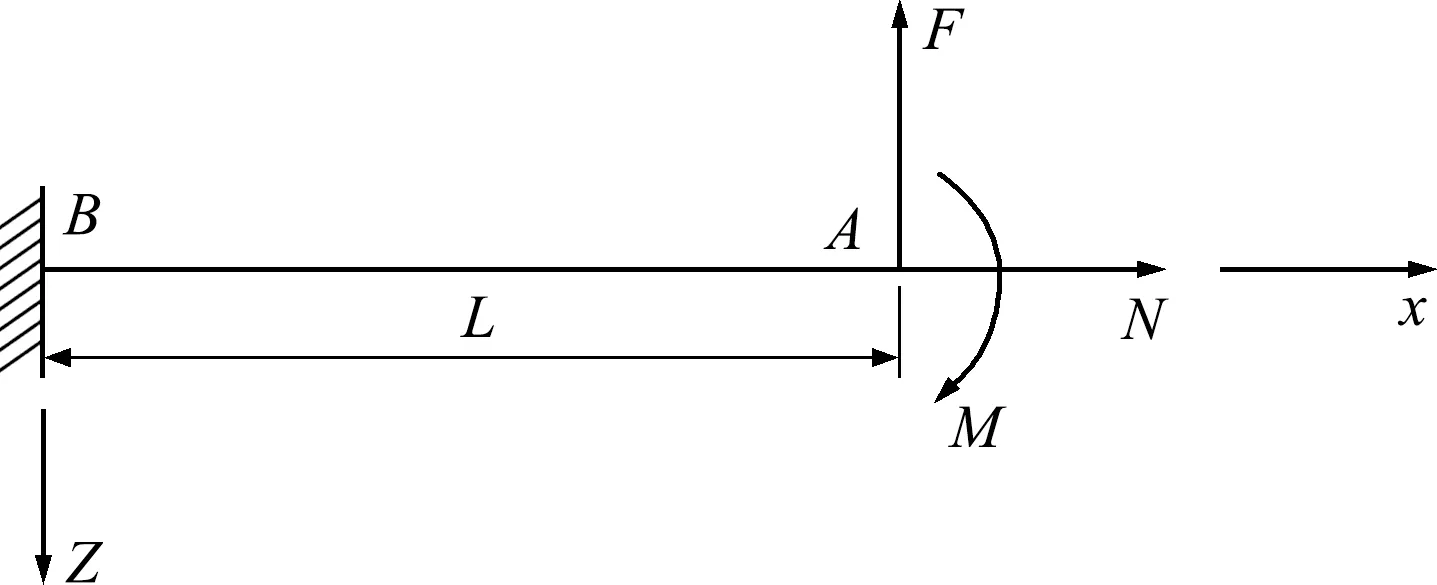
图2 蜂窝胞壁受力
首先,计算蜂窝胞壁弯曲变形的挠度,胞壁的位移场可表示为
(4)
式中u,v和w分别为x,y和z方向位移。
将式(4)代入式(2),可得
(5)
将式(5)代入式(1),可得
σx x=C11(l2zwI V-zw″)
σy y=σz z=C21(l2zwI V-zw″)
(6)
σx x=E11(l2zwI V-zw″)
(7)
最小势能原理可表示为式(8),计算挠度时可忽略轴向力的作用,推导出在F和M作用下的控制方程和边界条件。
δπ=δ(U-V)=0
(8)
式中
(9)
(10)
可得控制方程为
EI(l2wV I-wI V)=q
(11)
由于胞壁未受均布力作用,则式(11)中q=0。求解式(12)得到
(12)
代入下列边界条件
δw(0)=0,V≡EI[w‴-l2wV],δw′(0)=0
在x=L处,
M=EI[w″-l2wI V]=M
w″(0)=0,w‴(L)=0
(13)
可解得,系数C1,C2,C3,C4,C5和C6分别为
c1=-(eL /lFl-FL+M)/[(1+e2L /l)EIl2]
c2=eL /l(Fl+eL /lFL-eL /lM)/[(1+e2L /l)EIl2]
c3=F/(EI),c4=-(FL-M)/(EI)
c5=[2eL /lFl2-[(1-e2L /l)(FL-M)l]/
[(1+e2L /l)EI]
c6=-l2(FL-M)/(EI)
(14)
4.1 Ec x的求解
设x方向面内等效弹性模量为Ec x,图3给出了胞元在x方向受单向应力σx作用的示意图。
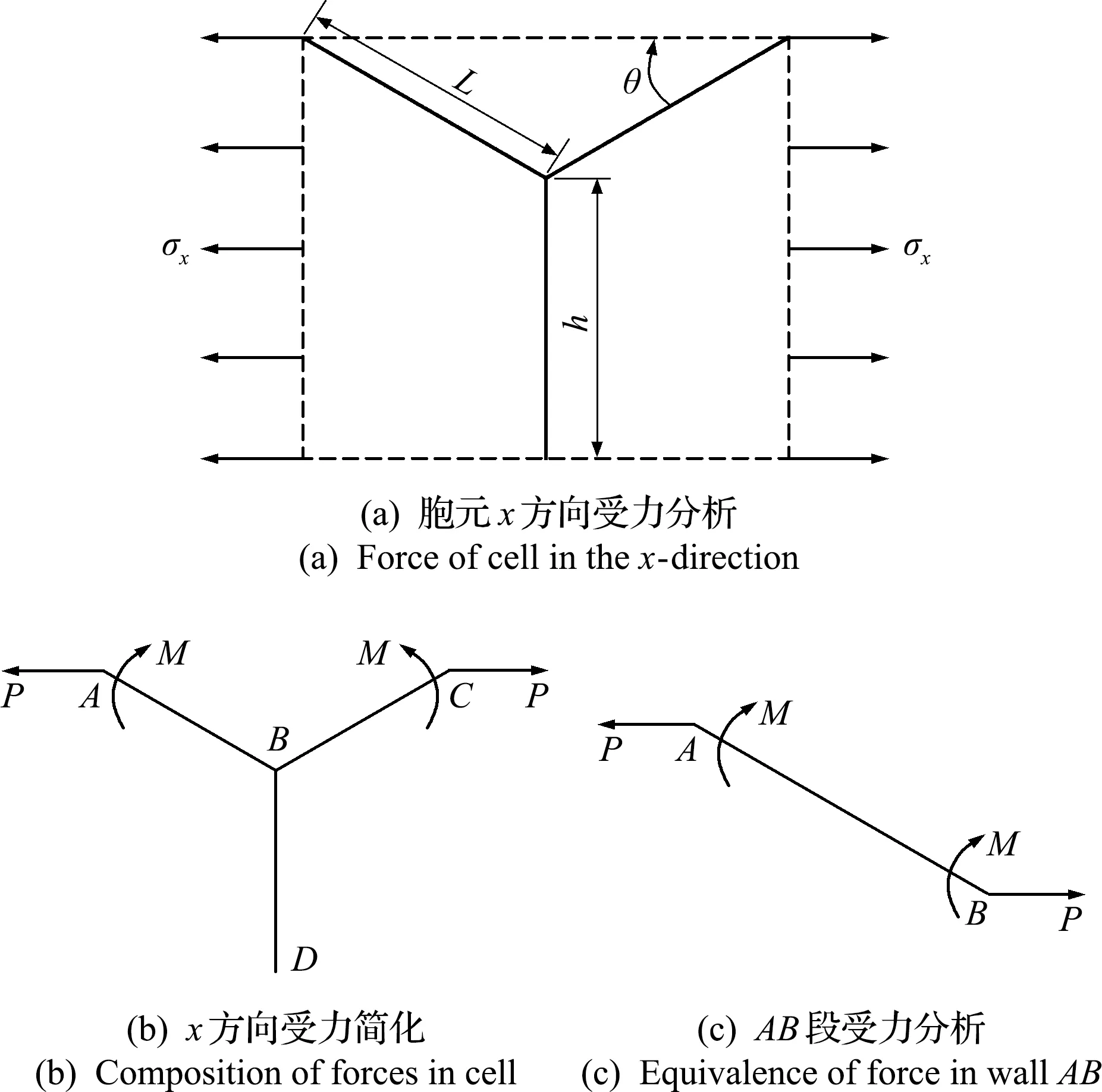
图3 胞元受x方向应力σx作用
由图3可得
P=σxb(h+Lsinθ)
(15)
由点A处力矩平衡可得
(16)
从中选取AB段做分析,将其简化为图2所示悬臂梁,将P分别按F方向和N方向分解,得F=Psinθ,N=Pcosθ。
AB段弯曲应变能与F和M的外力功相等,即
(17)
因为AB段轴向应变能只与N有关,故
(18)
AB段的总应变能为
UA B=UA B 1+UA B 2
(19)
BC段应变能与AB段相同,单位厚度的等效体变形能为
(20)
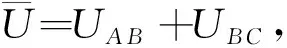
(21)
式中R=1/(h+Lsinθ)
当I=t3/12,A=t,h=L,θ=π/6时,可得正六边形蜂窝的面内弹性模量为
12l2L/cosh(L/l)+L(L2+3t2)]
(22)
4.2 Ec y的求解
设y方向面内等效弹性模量为Ec y,图4给出了胞元受y方向单向应力σy作用时的等效模型。
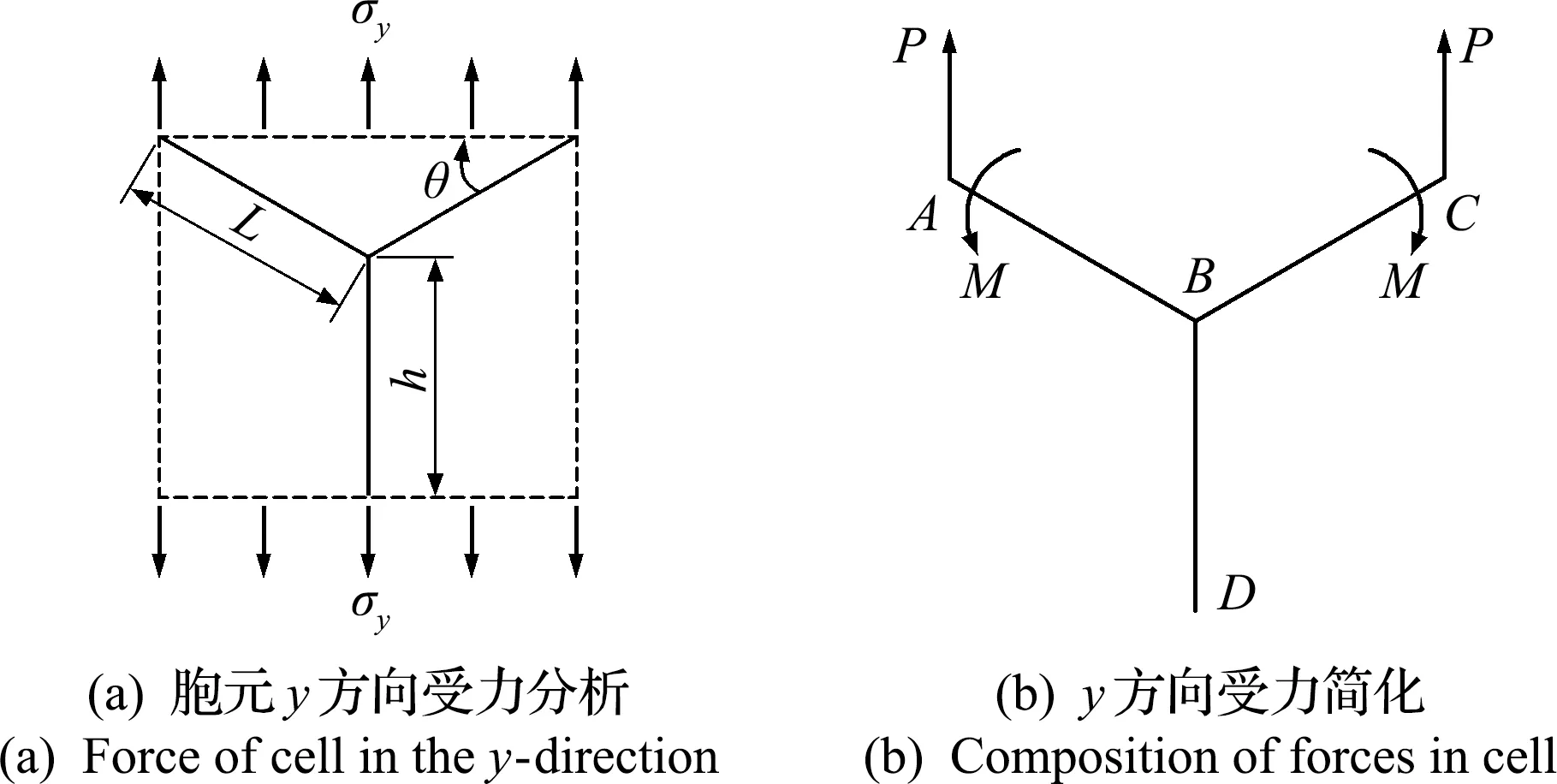
图4 胞元受y方向应力σy作用
由图4可知
P=σybLcosθ
(23)
在点A处力矩平衡,即
(24)
从中选取AB段做分析,将其简化为图2所示悬臂梁,将P分别按F方向和N方向分解,即F=Pcosθ,N=Psinθ。
AB段弯曲应变能与F和M的外力功相等,即
(25)
因为AB段轴向应变能只与N有关,故
(26)
AB段总应变能为
UA B=UA B 1+UA B 2
(27)
BC段总应变能为
UB C=UA B
(28)
BD段的轴向应变能为
(29)
单位厚度的等效体变形能为
(30)
式中β=h/L。
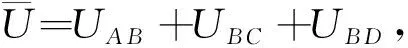
(31)
当I=t3/12,A=t,β=1,θ=π/6时,可得正六边形蜂窝的面内弹性模量为
(32)
4.3 Gc x y的求解
图5给出了剪切应力τ作用时胞元等效模型的受力状态。该模型需要满足下列条件。
(1)A,B和C三个节点都没有发生相对位移。
(2) 图5中各个节点的转角都相等。
(3) 剪切变形是因为BD段绕点B的转动以及BD段的弯曲造成的。
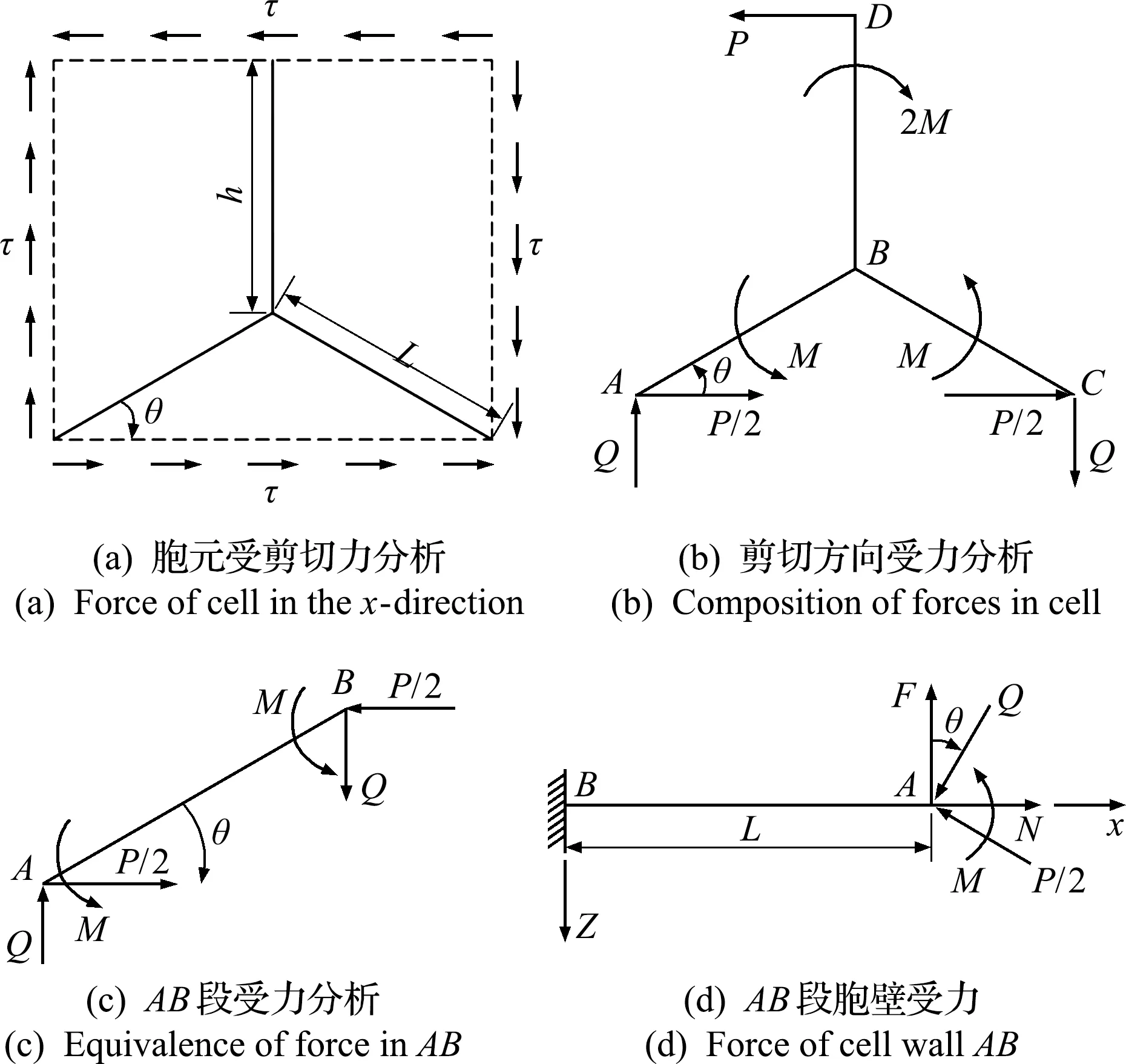
图5 胞元受剪切应力Gx y作用
由图5可知
(33)
因为AB胞壁对点B的合力矩为零,即
ΣMB=0,M=Ph/4
(34)
将P和Q按AB分解为沿轴方向力N和垂直轴向力F,即
(35)
因为BC段和AB段的受力形式相同,且AB段弯曲应变能与F和M的外力功相等,故
(36)
又因为AB段轴向应变能只与N有关,故
(37)
AB段总应变能为
UA B=UA B 1+UA B 2=UB C
(38)
BD段轴向应变能
(39)
单位厚度等效体的应变能为
(40)

(41)
5 算例分析
算例1考虑一个正六边形微尺度蜂窝,弹性模量E=68.97 GPa,蜂窝长度L=20 μm。可由等式(22,32)计算等效后的模量Ec x和Ec y,可以看出,x方向与y方向等效模量相同Ec x=Ec y,这是因为正六边形蜂窝结构具有面内各向同性,这一结果与传统方法的结果一致。图6给出了不同尺度参数下胞壁厚度对等效模量的影响,横坐标为胞壁厚度t,纵坐标为应变梯度理论下的等效模量与经典理论下的等效模量的比值,其中,图6(a)为拉伸模量Ec x/Ec x _ c,图6(b)为剪切模量Gc x y/Gc x y _ c。当尺度参数为0时,本文模型预测出的等效模量与文献中基于传统方法的结果一致。当厚度t较小时,等效模量表现出明显的尺度效应,这与传统的宏观模型不同。随着t的增加,尺度效应对等效模量Ec x,Ec y和Gc x y的影响逐渐减弱。

图6 不同尺度参数下t对等效模量的影响
算例2考虑一个正六边形微尺度蜂窝,材料参数为弹性模量E=106.4 GPa,尺度参数l=0.843 μm。本文计算了不同胞壁长度与胞壁厚度比值L/t(t的值保持不变为t=1 μm,变化L的值)时各个等效模量的值,结果如图7所示。其中,横坐标为L/t,纵坐标为等效模量。可以看出,随着L/t的增加,等效模量的值单调递减,由于尺度效应的存在,本文结果总是大于传统宏观模型。但是当L/t增大到8以后,两种理论预测的结果趋于一致,说明当胞壁长度很大的时候,尺度效应可以忽略。

图7 蜂窝胞壁长厚比对等效模量的影响
5 结 论
本文基于单参数应变梯度理论发展了一种能够计及尺度效应的微纳米蜂窝等效模量计算的新方法。蜂窝模量的尺寸效应主要与胞壁厚度有关,当厚度较小时尺度效应非常显著,此时基于本文方法预测出的模量会明显高于传统方法,而当胞壁厚度增大时,尺度效应变得微弱。需要注意的是,尺度效应还与胞壁的长度/厚度比有关,当长度/厚度比很大时,本文解与经典宏观解一样都非常接近于0,从工程角度来看此时尺度效应对计算结果的影响并不显著。另外,本文提出的计算方法只含有一个尺度参数,减小了未来应用于工程的阻碍。同时在宏观尺度下,本文方法能够自然地得到与传统宏观方法一致的解,因此有着良好的普适性。

