温度效应对覆冰导线舞动特征的影响研究

沈祺航， 刘小会*,2， 闵光云,3， 伍 川， 张 博

(1.重庆交通大学 土木工程学院，重庆 400074；2.重庆交通大学 省部共建山区桥梁及隧道工程国家重点实验室，重庆 400074；3.中山大学 中法核工程与技术学院，珠海 519082； 4.国网河南省电力公司电力科学研究院,郑州 450052)

1 引 言

覆冰导线舞动会使得金具磨损及线路破坏，严重阻碍线路的正常运行，给国民经济带来巨大损失[1]。由此可知，研究覆冰导线舞动对开发防舞、抑舞技术具有重要的工程实用价值。由于实验代价昂贵，人们经常采用数值模拟研究覆冰导线舞动特征。杨威等[2]利用Abaqus模拟覆冰二分裂导线的舞动，研究相间间隔棒对不同排列方式的导线防舞效果。刘小会等[3,4]系统地研究了覆冰四分裂导线舞动特征，使用直接离散法或间接离散法离散动张力应变，发现不同离散法下覆冰四分裂导线位移响应存在一定的区别；不同自由度下覆冰四分裂导线的位移响应也有明显区别。楼文娟等[5]研究六分裂覆冰导线舞动特性与风速和频率等关系，判定了输电线线路的起舞风速。杨晓辉[6]利用Abaqus有限元软件建立覆冰六分裂导线模型，对双摆防舞器的设计与使用提出改进方案。

大部分学者研究覆冰导线舞动时没有考虑温度效应的影响，为计算方便,用近似模态来作为导线面内模态[3，4,7]。赵珧冰等[8]研究指出索力和频率对温差变化十分敏感。这些分析说明研究覆冰导线舞动时有必要考虑温度效应和不同面内模态的影响。

本文建立考虑温度效应的覆冰导线舞动简化模型，推导并求解对应的舞动方程。根据数值模拟结果分析了温度效应对覆冰导线张力、频率和舞动特征的影响，并比较使用不同面内模态时覆冰导线时程曲线的区别。

2 覆冰导线的舞动方程

建立两端铰接的覆冰导线简化模型，如图1所示。以左悬挂点为原点建立笛卡尔坐标系O-x-y-z，两铰接点连线为x轴，y轴正方向垂直于x轴向下，z轴正方向垂直于x和y决定的平面向内。

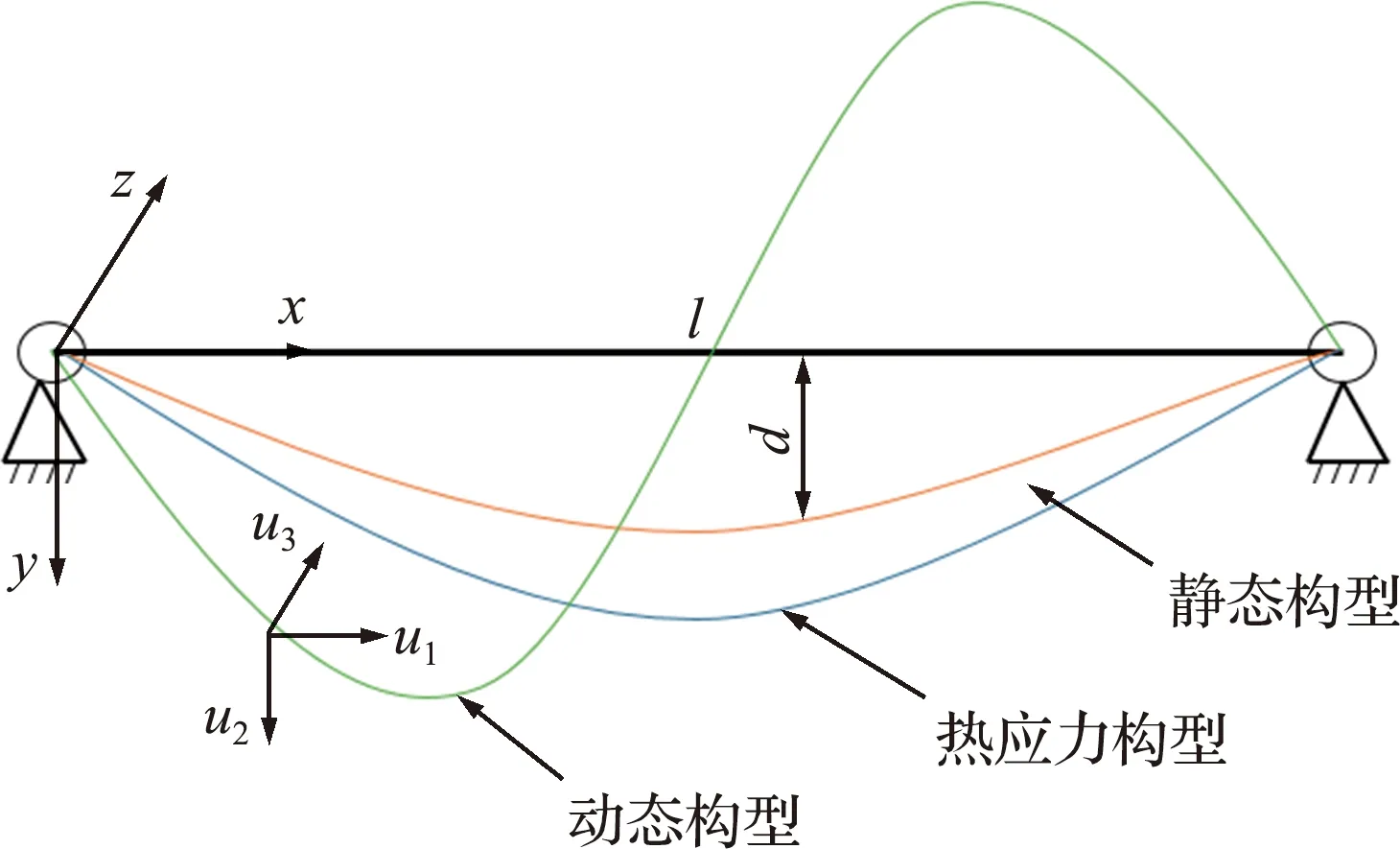
图1 单跨导线模型

图1中l为导线档距，d为导线垂度。x，y和z表示静态位移，u1，u2和u3表示x，y和z方向的动态位移。

为简化计算，本文根据实际情况做以下假设。

(1) 忽略覆冰导线的弯曲刚度和剪切刚度；忽略覆冰导线的轴向运动和扭转运动。

(2) 假设垂跨比d/l<1/8，即可采用抛物线构型描述导线的静态构型。静态构型y和垂度的表达式分别为

(1)

式中g为重力加速度，m为导线单位长度质量，H为导线静态水平张力。

(3) 假设覆冰均匀分布在导线上，不计覆冰的质量；假设温度应力沿导线横截面均匀变化。

(4) 忽略温度变化对弹性模量、阻尼系数和边界条件的影响。

2.1 静态构型中的平衡方程

覆冰导线只受重力时，静态的平衡方程可表示为

(2)

式中ds为导线微元长度，N1为导线的切向张力，在弧垂较小时可近似认为ds≈dx，N1≈H。

2.2 热应力状态的平衡方程

覆冰导线受温度影响后会形成新的热应力构型[9]，热应力状态下的平衡方程可表示为

(3)

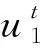
(4)

式中p1和p2为初始温度和变化后的单位荷载，α为热膨胀系数，t1和t2为初始温度和变化后的温度，E为弹性模量，A为横截面面积。

2.3 动态构型

覆冰导线在受风荷载下形成动态构型，动态的平衡方程可表示为

(5)

式中u1和u2为由风荷载引起的x和y方向上位移，N3为覆冰导线的动张力，可表示为

N3=EAε

(6)

式中ε为动应变，而每个位置的动应变其实差别不是很大，所以ε可表示为

(7)

根据三种不同构型的平衡方程得到覆冰导线的非线性振动方程组,

(8a)

(8b)

使用模态截断法把位移函数分离成一阶模态函数Ψ2(x)和Ψ3(x)与振型函数q2(t)和q3(t)的乘积。

u2(x,t)=Ψ2(x)q2(t)，u3(x,t)=Ψ3(x)q3(t)

(9)

将式(9)代入式(8)，应用伽辽金法把偏微分方程组(8)转化为常微分方程组，得到覆冰导线二自由度振动方程组为

(10a)

(10b)

篇幅所限，各项系数表达式不一一列举。

在求解式(5)时只考虑线性项，并根据导线的位移边界条件可得面内精确模态的表达式为

(11)

在式(11)的正对称模态时，包含频率的超越方程表达式[12]为

(12)

式中λ2=(EA/H)(mgl/H)2，λ为与垂度相关的Irvine参数[13]。

3 覆冰导线气动荷载特性

3.1 建立气动荷载模型

研究舞动及其防治技术的前提条件是确定覆冰导线的气动力荷载[14]。本文基于以下假设建立如图2所示的新月形覆冰导线横截面的模型。

图2 覆冰导线横截面

(1) 平均风沿z轴水平方向从左向右吹过来。(2) 覆冰的形状是新月形；厚度和形状延导线保持不变。(3) 基于准定常理论，不考虑导线运动对气动参数的影响。

图2中PD和PL是平均风引起的阻力和升力，PD方向与相对风速的方向一致，PL方向与PD垂直向上。U为平均风速，Ur为相对风速，α为风攻角，α0为初始风攻角。

根据空气动力学理论，覆冰导线无量纲的气动力系数定义为

(13)

式中Cy和Cz分别为y和z方向的升力系数和阻力系数，ρ为空气密度，D为裸导线的直径。

3.2 气动力系数

刘小会等[4]进行风洞试验，获得了在风速 18 m/s，风攻角α=55°，冰厚12 mm时气动力系数的数据。通过三次曲线拟合测得的数据可以得到气动力系数表达式为

Cy=-0.9606α-1.40716α2+97.62315α3

(14a)

Cz=2.39795α-7.00826α2-119.95612α3

(14b)

将式(14)代入式(13)得y和z方向的升力及阻力表达式为

(15a)

(15b)

把式(15)代入式(10)得

(16a)

(16b)

4 多尺度法对非线性方程求解

覆冰导线的舞动问题属于弱非线性振动问题，对于弱非线性问题的分析，多尺度法可以计算其稳态响应和暂态响应。利用多尺度法求解式(16)得

(17a)

(17b)

(17c)

式中a2和a3为舞动幅值，θ2和θ3为初始相位，令式(17)等式右边为零可以得到覆冰导线的稳态幅值。

5 数值算例及结果分析

本文选择LGJ-400/50钢芯铝绞线，各项物理参数为导线的长度300 m，单位长度质量1.511 kg/m，重力加速度9.8 m/s2。横截面积599.5862 mm2，弹性模量6.9×104N/mm2。裸导线直径27.63 mm，初始张力2.9308×104N，y方向的阻尼比0.067×10-2，z方向阻尼比 0.067×10-3，空气密度 1.2929 kg/m3,风速18 m/s，热膨胀系数 19.3×10-6℃-1。

钢芯铝绞线会因为温度变化产生热胀冷缩现象，从而改变垂度和张力的值，进而导致舞动特征改变。由于导线一阶振动频率振幅比较大，与Irvine参数密切相关，图3给出了当覆冰导线在温度均匀变化的情况下，一阶正对称模态频率与Irvine参数的关系图。

图3 温度变化对Irvine参数与无量纲频率λ之间的关系曲线

图3所示频率随着λ的增加而增加，降温40 ℃时，频率变化最大相差28.4%；Irvine参数λ较小时，温度变化对频率影响不明显；Irvine参数λ增大到一定范围时，温度越低则频率越低；Irvine参数λ较大时，温度变化对频率影响也不明显。这是由于导线频率对温度的敏感性取决于导线的长宽比。在导线垂度较小或者较大时，导线的频率对温度敏感性都不高，这与使用有限元方法得出的结论相吻合[11]。

本文选择四种常见的初始张力来研究温度变化对张力比值的影响。

图4所示覆冰导线不同初始拉力时，温度对张力比值的影响并不一致。当覆冰导线初始张力为2×104N，降温40 ℃时，张力的比值变化最小为20.51%；而初始张力为4×104N，降温40 ℃时，张力的比值变化最大为40.4%。降温使得导线张力增大，与实验结果和实际工程相符[15，16]。这是由于求解式(4)可以得知温度下降对张力的影响很大。当初始张力在某一范围时，降温会导致张力变化更大。

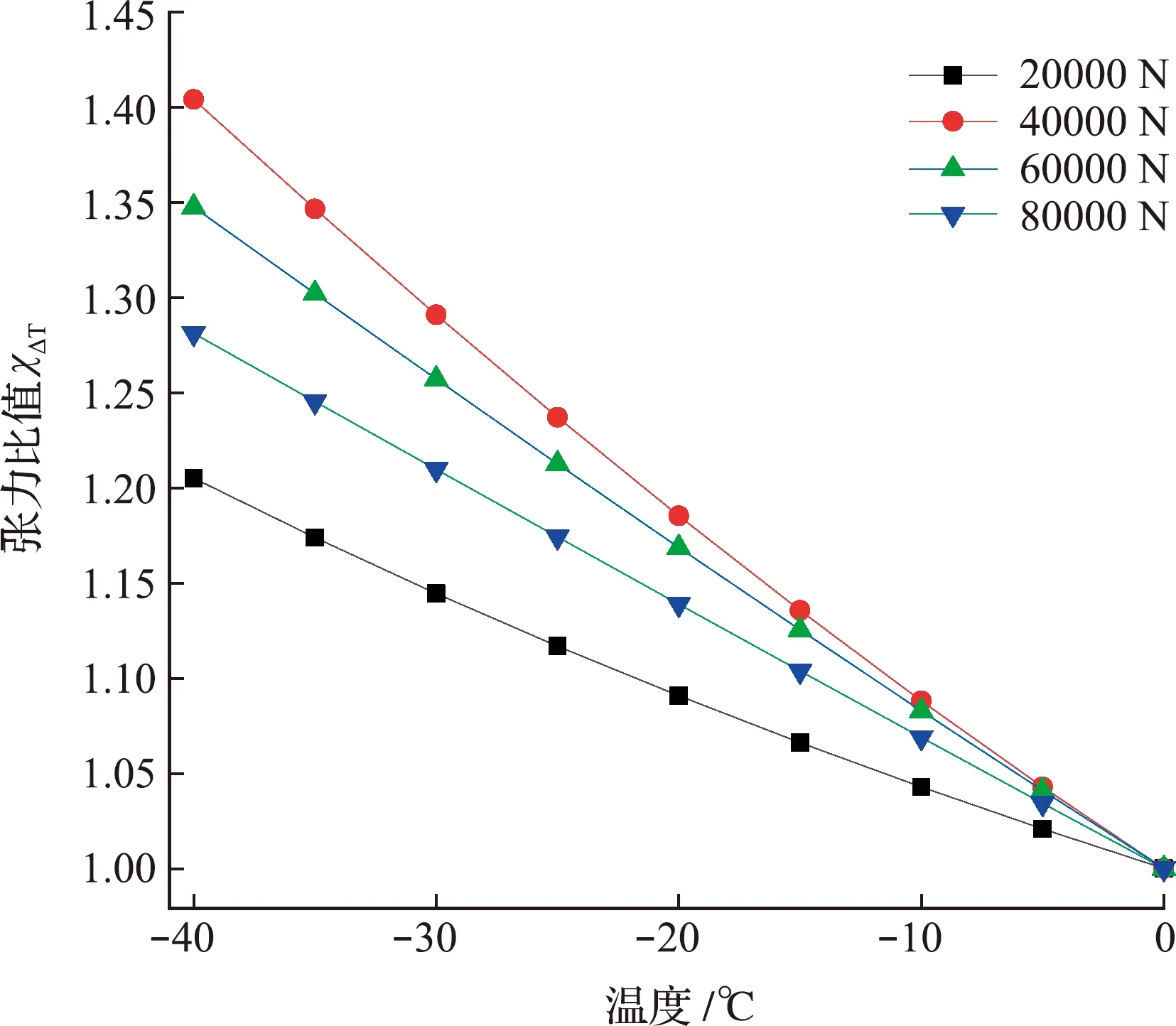
图4 温度变化对输电线张力比值的影响

由式(11)可知模态中包含频率，所以使用不同模态计算幅值会有误差，为了比较面内使用不同模态对覆冰导线时程曲线的影响，本文采用数值模拟方法，如图5和图6所示，面外模态都用Ψ3(x)=sin(πx/l)。

图5所示黑色曲线是采用精确模态式(11)计算得到的舞动时程曲线。当弧垂比较小时，部分学者也使用面内的近似模态,Ψ2(x)=sin(πx/l)，使用近似模态计算得到的舞动时程曲线见红色曲线。在前40 s，两种模态下面内幅值很接近。近似模态下覆冰导线舞动在80 s左右趋于稳定，精确模态下在60 s时就趋于稳定，两者相差33.3%。趋于稳定时，近似模态下覆冰导线面内幅值接近0.95 m，而精确模态覆冰导线接近0.46 m，两者相差106.5%。近似模态下圆频率2.49，精确模态下圆频率2.52，两者相差1.1%。

图5 面内位移响应

使用多尺度法得到近似模态下面内稳态幅值0.94 m，精确模态面内稳态幅值0.45 m，结果与龙格库塔函数求得的幅值基本一致。

图6所示两种模态下的覆冰导线舞动都在70 s左右时趋于稳定。在面外位移响应趋于稳定前，精确模态的幅值略大于近似模态；在趋于稳定后，两种模态的幅值都接近0.23 m。由此得知面内使用不同模态对覆冰导线面外舞动影响并不大。

图6 面外位移响应

本文使用精确模态作面内模态，得到覆冰导线舞动已经稳定时，三种温度下的位移时程曲线图。

图7所示，温度降低使覆冰导线舞动的周期减小，面内位移增大。在0 ℃时，覆冰导线的幅值接近0.43 m，周期2.51。在-40 ℃时，覆冰导线幅值接近0.46 m，周期2.73。从0 ℃降温到-40 ℃，两者幅值相差6.97%，周期相差8.76%。

如图8所示，在0 ℃时，覆冰导线幅值接近 0.23 m，周期2.56。在-40 ℃时，覆冰导线幅值接近0.31 m，周期2.46。从0 ℃降温-40 ℃，两者幅值相差34.78%，周期相差3.90%。

图8 温度对面外位移响应曲线的影响

6 结 论

本文建立了考虑温度影响的覆冰输电线舞动控制方程，分析了温度效应对导线张力及第一阶对称模态对应的频率的影响，进一步使用多尺度法和数值方法研究了温度变化对覆冰导线舞动特征的影响，研究结果如下。

(1) 温度对第一阶对称模态对应的无量纲频率有显著的影响，而对无量纲频率影响的强弱与Irvine参数λ有关。

(2) 温度对覆冰输电线的张力影响十分显著，温度对导线张力影响大小主要取决于初始张力的一定范围内。

(3) 温度下降后覆冰导线的面内舞动幅值变化不大，但面外舞动幅值显著增加；面内舞动周期增大，面外舞动周期减小。另外近似模态与精确模态计算得到的舞动幅值相差较大，所以舞动分析时应选用精确模态。