基于参变量变分原理的直升机系留载荷高性能计算方法
张燕辉, 高 强
(1.中国直升机设计研究所,景德镇 333001;2.大连理工大学 工程力学系 工业装备结构分析国家重点实验室,大连 116024)
1 引 言
当直升机在舰船上停留或者在机库长期存放时,通常要承受因舰船运动产生的惯性力、直升机重力作用和风载等载荷作用,这些载荷可能会引起直升机在舰船上发生侧翻或滑移,从而使直升机受损。为了保证直升机安全地停放在舰船上,就必须使用系留装置将直升机系留在舰船上,这就需要对直升机的系留索具和系留接头上的载荷进行分析,从而给出合理的系留方案,使直升机和系留设备上承受的载荷比较均匀和合理。
分析舰载直升机的系留系统,不仅要判别索具的拉伸和松弛状态,而且还需考虑起落架的变形。当索具受拉伸荷载作用时,其与普通杆件没有区别;而当索具受压缩荷载作用时,因无法承受压力作用出现松弛而失效。对于起落架,当其受到压缩载荷作用时,与普通杆件没有区别;而当起落架受到拉伸荷载作用时,起落架离开地面不承力而失效。因此,索具和起落架分别在受拉和受压时表现出的强非线性特征,是直升机系留系统的一个显著特点。同时,由于索具和起落架的变形,将导致整个系统发生较大变形和转动,这意味着直升机系留问题还必须考虑结构大变形。一般情况下,系留索具的数量往往要多于直升机机体的运动自由度,直升机系留问题本质上属于超静定问题。对于直升机系留问题表现为材料和几何双重非线性特征,需要针对这类问题发展有效的求解算法。目前关于系留载荷的计算方法主要有矩阵力法、有限元法和能量法等。早期关于系留载荷的计算通常采用矩阵力法[1]求解,但需要先判断索具拉压状态,采用矩阵力法求解较繁琐,且不便于实现程序化。随着有限元法在飞机设计过程中的广泛应用,利用有限元法计算系留载荷已成为重要手段,而且通常借助成熟的商业软件对系留问题进行模拟,如NASTRAN[2],ABAQUS[3]和ANSYS[4]等。主要方法是,机身采用刚体单元模拟,索具采用拉压刚度不同的杆单元模拟,而起落架采用间隙单元模拟。尽管利用有限元法计算系留载荷能够获得相对较准确的计算结果,但在一些特殊情况下会发生不收敛现象。另一类求解系留载荷的重要方法是能量法,该方法主要思想是利用能量原理建立平衡方程后,采用迭代方法进行求解。文献[5]利用能量原理对系留索具载荷进行求解,但并没有考虑起落架的弹性变形和机身的转动。在此基础上,文献[6]对其进行了改进,考虑了起落架的弹性变形,而且增加了机身转动自由度。文献[7]基于虚功原理推导了机体刚体位移方程组,并采用牛顿迭代法求解非线性方程组。基于能量原理的计算方法在求解直升机系留载荷方面有两个难点。一方面,不容易判断索具和起落架的拉压状态;另一方面,由于该问题具有材料和几何双重非线性,计算需要不断迭代,容易发生不收敛。
目前关于我国舰载直升机系留问题,大部分采用ABAQUS和NASTRAN软件进行分析,存在较多困难。首先,直升机在舰船停放时,会受到舰船运动的惯性力、直升机重力和风载等载荷作用,因此不同的系留方案、直升机重量状态、航速、浪向和风载方向,组合后的工况数量较多,可达几万甚至几十万种工况,当采用有限元软件批处理分析时,需要不断读取软件产生的结果数据文件,会耗费较多的计算时间。每更新一次系留方案,几天甚至几十天才能给出计算结果,严重影响任务进度。其次,ABAQUS和NASTRAN软件在计算非线性问题时,在一些工况下会发生不收敛,因此在进行批处理时,对于不收敛工况,需要挑选出来后将间隙单元改成杆单元或弹簧单元计算,从而导致计算结果与实际偏离较大,而且由于该过程需要挑选不收敛工况,处理过程复杂繁琐,计算效率低,无法满足目前的型号需求。最后,由于需要不断读取软件计算结果文件,效率较低,因而无法对系留方案进行优化设计。本文针对以上难点,基于参变量变分原理提出了计算系留载荷的新方法。该方法具有高效、收敛性好和方便实现程序化等优点。
参变量变分原理是由钟万勰等[8]提出的,并广泛应用于弹塑性[9]、接触[10]和摩擦[11]等非线性问题分析,在求解拉压刚度不同的杆件系统时非常有效[12]。舰载直升机的系留问题可简化为由机身、索具和起落架组成的拉压刚度不同的杆件系统。本文将机身简化为刚体,并利用参变量变分原理建立了机体重心处的平衡方程组,同时考虑了索具和起落架的材料非线性以及结构大变形。利用参变量变分原理引入参变量和松弛变量,从而准确地判断索具和起落架的拉压状态,将索具和起落架拉压刚度不同的材料非线性问题转换为线性互补问题求解,从而极大地提高了结果的收敛性。
2 直升机系留模型简介
舰载直升机系留方式如图1所示,系留系统由机身、索具和起落架组成。索具一端与机身系留点连接,另一端与舰船甲板上的系留窝连接;起落架一端与机身连接,另一端与舰船甲板接触。机身简化为刚体,索具和起落架可通过拉压刚度不同的杆单元模拟。

图1 直升机系留
索具只能承受拉伸荷载作用,当索具处于拉伸状态时,其受轴向拉力;当索具松弛或未变形时,索具不受力。起落架和索具的重量相对于直升机重量非常微小,可忽略不计。同时假设起落架可以沿着水平方向运动,且不考虑摩擦力影响。设索具的数量为N,则第i(i=1,2,…,N)根索具的本构关系如图2(a)所示,可表示为
(1)

(2)


图2 索具和起落架的本构关系
在风浪较大时,直升机系留装置可能会受到较大载荷,导致索具和起落架的变形较大。因此对于直升机系留问题,不仅要考虑结构本身的材料非线性,而且还要考虑因结构发生大变形而导致的几何非线性,这表明直升机的系留问题表现出较强的非线性特点,结果很容易发生不收敛现象。本文在考虑结构大变形的情况下,利用参变量变分原理,将拉压刚度不同杆件的材料和几何双重非线性问题转换为仅考虑几何非线性的互补问题,从而极大地提高了结果的收敛性。
3 基于参变量变分原理的系留载荷分析
3.1 拉压刚度不同杆件的参变量变分原理
对于任意一根拉压刚度不同的杆件(不考虑索具预紧力和初始变形),假设杆件的拉伸和压缩刚度分别为K(+)和K(-),且K(+)≠K(-),则杆件的本构关系为
F=KΔl
(3)
式中F为杆件轴向力,Δl为杆件变形量,且
(4)
当K(+)>K(-)时,本构关系(3)可表示为
F=K(+)(Δl+λ)
(5)
式中λ为参变量,
(6)
式(6)与互补关系(7)等价,即
(K(-)-K(+))Δl-K(+)λ+ν=0
(λ≥0,ν≥0,λν=0) (7)
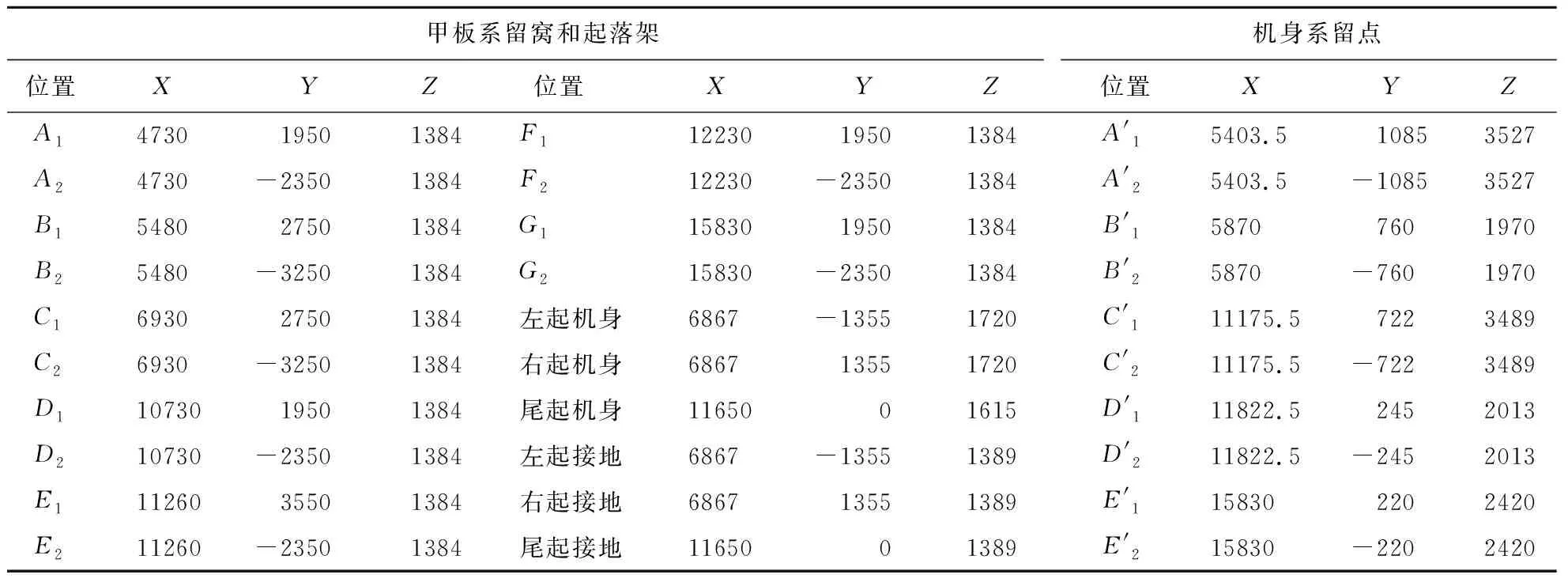
而当K(+) F=K(-)(Δl-λ) (8) 则要求 (9) 式(9)与互补关系(10)等价,即 (K(-)-K(+))Δl-K(-)λ+ν=0 (λ≥0,ν≥0,λν=0) (10) 上述两种情况下,对应的方程(5,7,8,10)可统一表示为 F=Kmax(Δl-sλ) sKmax-KminΔl-Kmaxλ+ν=0 (λ≥0,ν≥0,λν=0) (11) 式中s=sign (K(-)-K(+)),Kmax=max (K(-),K(+)),Kmin=min (K(-),K(+))。符号sign表示取符号,其定义为 (12) 容易证明,式(11)给出的参变量变分原理与式(3,4)给出的平衡方程等价,具体证明过程参见文献[13]。 (13) 式中δX=[δx,δy,δz]T,且 (14) (15) (16) (17) 通过参变量λi可判断索具的拉压状态,当λi=0时,索具处于拉伸状态;当λi>0时,索具处于松弛状态。Fi沿着x,y和z方向的分量分别为 (18) (19) 式中符号⊗表示两个向量的叉积运算。 (20) (21) (22) (23) 起落架压力对重心点的力矩为 Mj=Fj⊗(X′j-X0) (24) 整个结构的平衡方程可写为 (25) 再考虑约束条件 (26) (27) 式(26,27)分别对应于索具和起落架的约束方程。 根据以上推导,直升机系留载荷计算最终归结为求解带有约束条件(26,27)的关于方程组(25)的二次规划问题。由于式(25)为非线性方程组,需要通过迭代方法进行求解。本文在求解时运用MATLAB软件的fmincon函数,计算时选择序列二次规划算法(SQP)进行求解。通过带有约束条件(25~27)即可求参变量λ,然后根据方程(16,21)可分别计算出索具的拉力和轮胎的压力。 以某舰载直升机在舰船上的系留问题为例,证实本文方法的性能。直升机质量为6815 kg,利用机身上的10个系留点(A′,B′,C′,D′,E′,每侧各一点)布置14根系留索具,其中点B′和点D′,每个点2根;点A′、点C′ 和点E′每个点1根,舰船甲板上布置14个系留窝,机身左右两侧分别布置7个系留窝;起落架采用后三点布置,由左右两个主起落架和一个尾起落架组成,系留方案如图3所示,机身系留点、舰船甲板系留窝和起落架坐标列入表1。直升机重心坐标为(8512,1,3417)。索具的弹簧刚度为900 N/mm,主起落架的刚度为705.9 N/mm,尾起落架的刚度为437.5 N/mm。分别考虑3种不同的载荷工况,其对应的载荷数据列入表2,载荷作用于重心处。 图3 某型舰载直升机系留方案 为验证本文方法的性能,分别使用通用有限元软件NASTRAN和ABAQUS建立全机系留模型进行计算(不考虑预紧力和起落架初始压缩),并将计算结果与本文方法的计算结果进行比较,三种方法在计算时直升机机身均简化为刚体。本文算例均是在中央处理器为12核、32 G内存和主频3.6 GHz的计算机上进行。运用NASTRAN软件计算时,索具采用只承拉不承压的杆单元来模拟,而起落架采用Gap单元模拟;运用ABAQUS软件计算时,索具和起落架均采用非线性连接单元(Connector单元)模拟索具和起落架非线性刚度特性。三种工况下的计算结果分别列入表3~表5。 表1 机身系留点、甲板系留窝和起落架坐标(单位:mm) 表2 重心处作用三种载荷工况 表3 工况1:系留载荷计算结果(单位:N) 表4 工况2:系留载荷计算结果(单位:N) 表5 工况3:系留载荷计算结果(单位:N) 对于工况1,由表3可知,本文方法的计算结果与NASTRAN和ABAQUS软件的计算结果符合良好,所有索具和起落架的拉压状态均一致,这证实了本文方法的正确性。同时,表3还表明本文方法与ABAQUS软件的计算结果更接近,因为ABAQUS软件在求解非线性接触问题时精度更高。对于工况2,NASTRAN软件不收敛,无法进行计算,而本文方法和ABAQUS软件能够很好地收敛,并在表4中给出了对应的计算结果,可以看出结果符合良好;而对于工况3,ABAQUS软件不收敛,无法进行计算,而本文方法和NASTRAN软件能够很好地收敛,并在表5中给出了本文方法和NASTRAN软件的计算结果。以上分析表明,ABAQUS和NASTRAN软件在某些工况下可能不收敛,而本文方法具有较好的收敛性。 为了说明本文方法的高效性,在均采用并行计算的情况下,随着工况数量的增加,将本文方法与NASTRAN和ABAQUS软件批处理计算效率进一步比较。图4给出了NASTRAN软件批处理、ABAQUS软件批处理和本文方法随工况数量增加的CPU时间。可以看出,与NASTRAN软件和ABAQUS软件相比,本文方法具有非常高的计算效率,而且由于运用NASTRAN和ABAQUS软件批处理计算时需要读取结果命令文件,随着工况数量的增加,NASTRAN和ABAQUS软件的计算时间急剧增加,而本文方法方便实现程序化处理,且不需要读取其他软件的数据文件。因此,本文方法在计算多工况的直升机系留载荷时具有非常高的效率。 图4 NASTRAN软件、ABAQUS软件和本文方法的CPU时间 基于参变量变分原理建立了直升机系留载荷求解的有效方法,将由索具和起落架组成的拉压不同刚度的材料和几何双重非线性问题,转换为仅几何非线性互补问题求解,极大地提高了结果的收敛性。数值算例中,通过与NASTRAN和ABAQUS软件比较,结果表明,本文方法对于计算舰载直升机的系留载荷具有较好收敛性和较高计算效率。该方法对提高系留载荷计算效率、快速优化系留方案和设计直升机机身系留接头提供了更可靠的计算依据。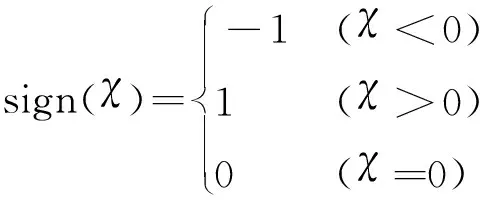
3.2 直升机重心平衡方程推导



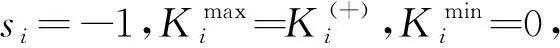





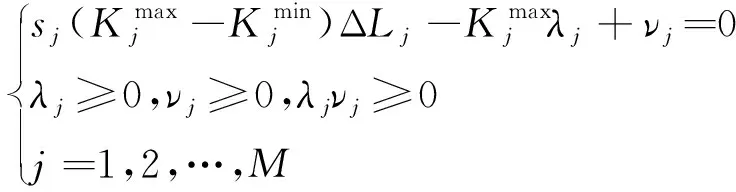
4 数值算例






5 结 论

