例谈有关两个参变量问题的几种解题方法
杨伟达
(广东省广州市花都区第二中学 510820)
在历年高考试题和模拟试题中常常出现一类涉及两个参变量的难题.这类试题主要考查参变量的求值或取值范围.它初看起来无从下手、思路不明,但仔细思量、推敲便会豁然开朗.笔者就有关两个参变量问题分别从线性规划、方程思想、几何性质、向量运算、不等式性质等多角度进行析疑解惑,从而体现出浓浓的“高考味”.现举例说明.
一、借用线性规划解决两个参变量问题
有这样的一类题,看似熟悉、简单的方程,却因含有两个参变量使得问题变得更加复杂,此时可根据题目的条件转化为一类不等式组,借助线性规划知识将问题解决.
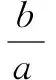
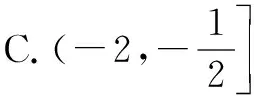
分析此题考查了含有两个参变量的一元二次方程根的分布情况.解决此题关键在于:将方程转化函数,运用函数的零点存在定理,借助线性规划知识将问题解决.
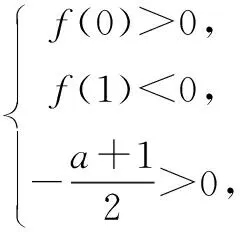
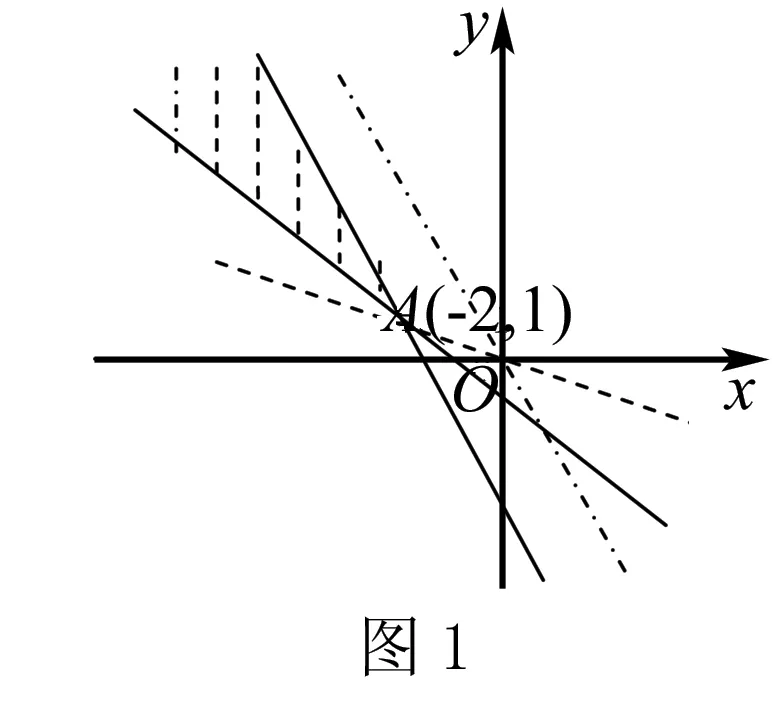
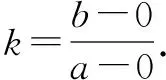
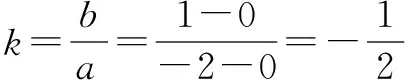
当直线经过原点与直线2a+b+3=0平行时,k=-2为最小
例2 已知函数f(x)=|xex+1|,关于x的方程f2(x)+2sinα·f(x)+cosα=0有四个不等的实根,则sinα-cosα≥λ成立,则实数λ的最大值为____.
分析此题考查了函数、方程、不等式、三角函数等多个知识点结合的综合题.本题难点:含有绝对值符号及两个参变量.解决此题的关键:重在转化,借助图形,利用线性规划知识将问题解决.
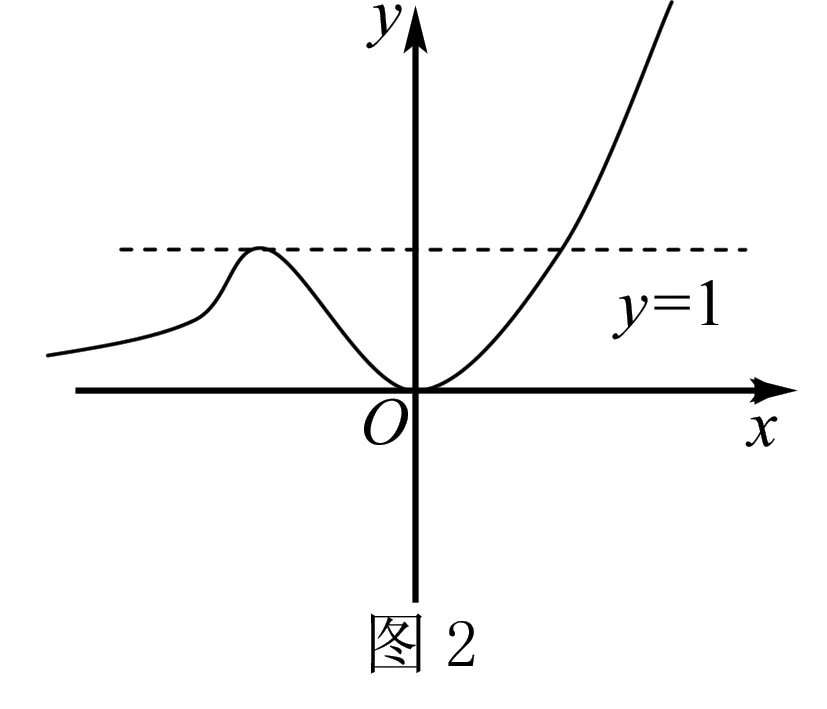
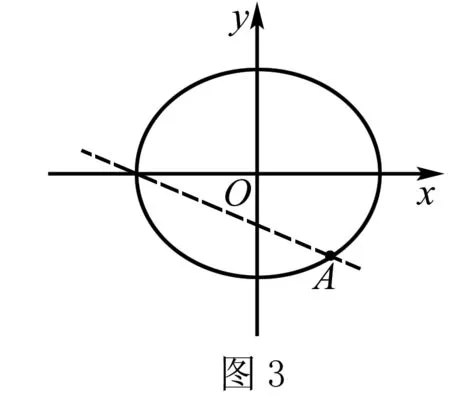
解如图2,f(x)=|xex+1|.
当x>0时,f(x)=xex+1,f′(x)>0,f(x)单调递增;
当x<0时,f(x)=-xex+1,令f′(x)=0,解得x=-1.
所以当x<-1时,f′(x)>0,f(x)单调递增;
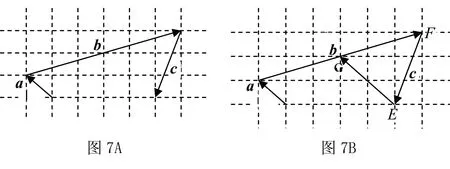
当<-1 有这样的一类题,看似熟悉、简单的函数,却因含有两个参变量使得问题变得更加复杂,此时可根据题目的条件把它转化为方程,借用方程组消元将问题解决. 分析此题涉及含有两个参变量的一元二次不等式.由于涉及两个参变量,难度增加,解决此问题关键:转化为一元二次函数,运用分类讨论,列方程组消元可求得两个参变量的值. 有这样的一类题,条件中涉及几何背景的知识,且含有两个参变量.此时,借用平面几何性质,观察图形特征,问题会更容易让人理解. 例4 (2009年高考重庆卷文)把函数f(x)=x3-3x的图象C1向右平移u个单位长度,再向下平移v个单位长度后得到图象C2,若对任意的u>0,曲线C1与C2至多只有一个交点,则v的最小值为( ). A.2 B.4 C.6 D.8 分析此题考查了函数图象的运动变化.困难所在:涉及两个参变量.问题是:在图象之间如何找到至多只有一个交点. 解决此题的关键:画出两个图象,观察图形,运用平面几何性质,找出极大值和极小值,进而找到参变量v的最小值. 解利用导数方法作函数f(x)=x3-3x的图象C1,如图4所示,然后作平移变换得到C2,观测图象只有在v≥f(x)极大值-f(x)极小值=4时对任意u>0(表示图象向右平移)曲线C1与C2至多一个交点.故选B. (1)求椭圆的方程;(2)若直线l:y=kx+m(k≠0)与椭圆相交于B,C两点(异于点A),线段BC被y轴平分,且AB⊥AC,求直线l的方程. 分析此题考查了直线与椭圆相结合的综合问题.第二问涉及两个参变量,若直接列方程组,方法简单,但运算复杂,学生只能可望而不可及;若从平面几何的对称性质,观察图形,问题会变得简单. (2)将直线方程y=kx+m代入椭圆方程, 整理,得(1+k2)x2+8mkx+4m2-8=0. 因为k≠0,所以m=0. 因为当m=0时,B,C关于原点对称,设B(x,kx),C(-x,-kx). 因为AB⊥AC,A(2,1), 有这样的一类题,条件中涉及到平面向量的基本定理.由于涉及含有两个参变量让人无从下手.解决此问题方法:一方面可以采用向量的加、减法原理求出两个参变量的值;另一方面也可以用数量积列出方程组求解.当然,有时采用法向量消元更加方便、快捷. 解如图6,(1)略.(2)∠BOC=360°-∠AOB-∠AOC=360°-150°-120°=90°, 所以∠COD=∠AOC-90°=120°-90°=30°, ∠BOD=360°-∠AOB-90°=360-150°-90°=120°. 分析对于这样的一个图,许多人自然会想到建立平面直角坐标系,利用向量的坐标运算可求得;若细心观察图形发现a是小正方形两端点的对角线,且向量c点的起点及向量b的中点都在小正方形的顶点上,平移向量a即可构成一个三角形,利用向量的三角形法则可得c=λa+μb(λ,μ∈R). 解析由图7B可知,向量b的中点经过点E(小正方形的一个顶点),向量c的起点F是小正方形的一个顶点,连接EF,构成一个三角形. 有这样一类题,条件中含有绝对值符号,若用去绝对值符号则需要进行分类讨论,加上涉及两个参变量,本来复杂的题变得难上加难.此时,恰当运用绝对值不等式性质会有意想不到的效果. 例8 设f(x)=|log2x+ax+b|(a>0)在区间[t,t+2](t为正数)上的最大值为Mt(a,b),若{b|Mt(a,b)>1+a}=R,则实数t的最大值( ). 分析此题考查了含有绝对值符号的函数.学生思维障碍是含有多个参变量及绝对值符号.解决此问题的关键:去绝对值不等式符号,应用其性质可以避免了分类讨论,此题就可快速解决. 总而言之,在涉及到多个参变量的创新型试题是培养学生能力、优化学生思维品质的极好素材,应引起广大师生足够重视.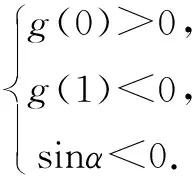
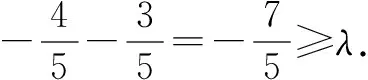

二、借用方程思想解决两个参变量问题
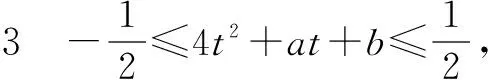
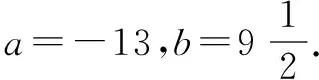
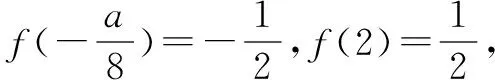
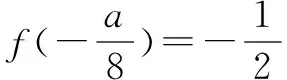
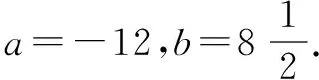
三、借用平面几何性质解决两个参变量问题
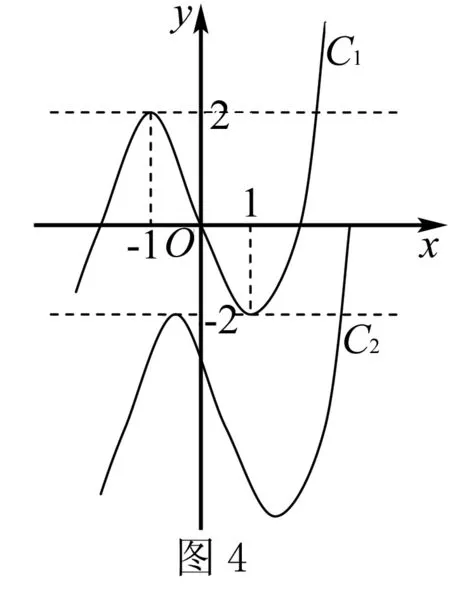
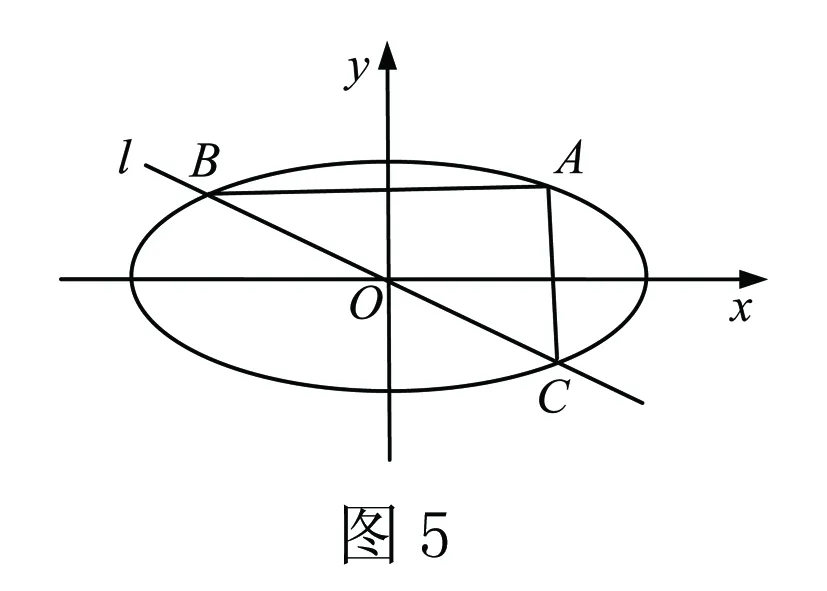
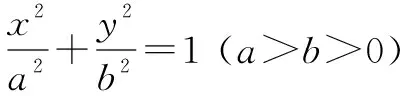
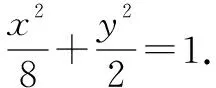
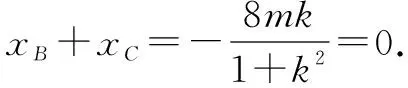
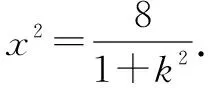
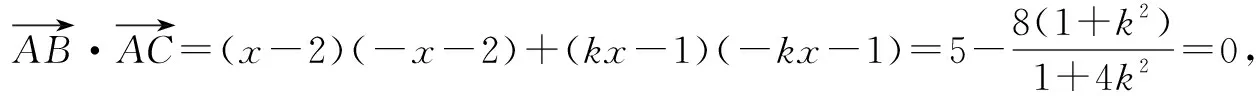
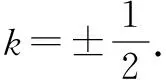
四、借用向量运算解决两个参变量问题
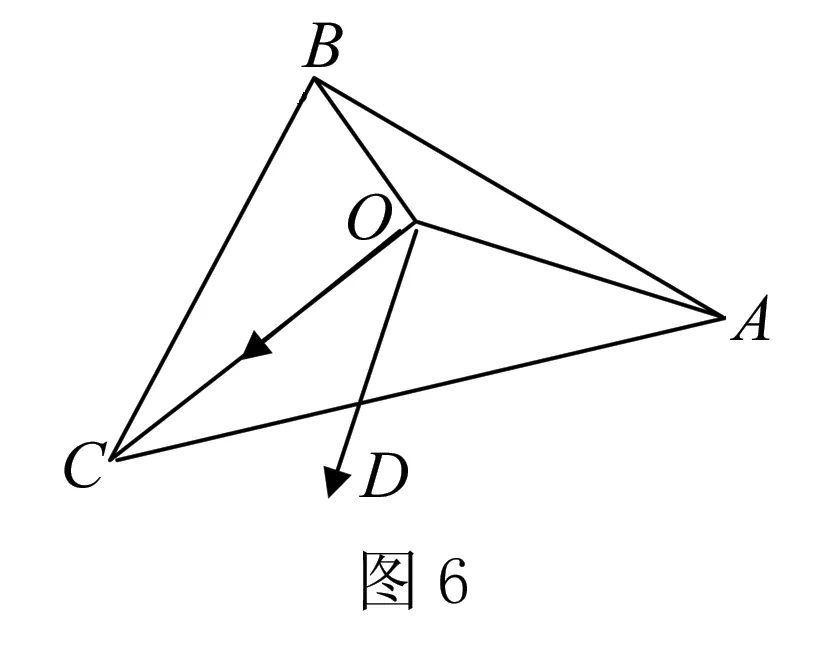
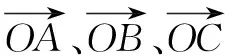
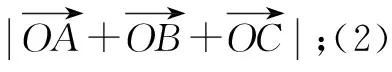
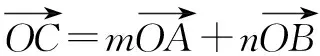
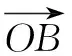
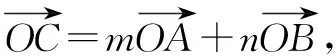
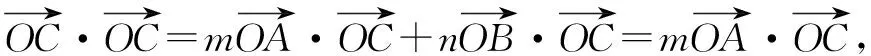
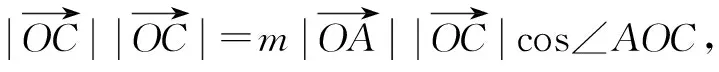
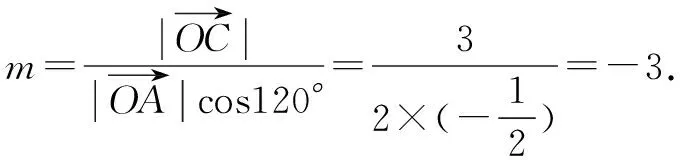
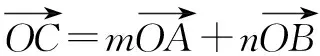
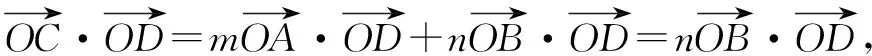
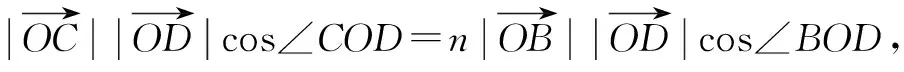
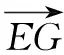
五、借用绝对值不等式性质解决两个参变量问题