Top-k集合空间关键字近似查询方法

孟祥福，王丹丹，张霄雁，贾江浩

1.辽宁工程技术大学 电子与信息工程学院，辽宁 葫芦岛 125105

2.辽宁工程技术大学 软件学院，辽宁 葫芦岛 125105

随着GPS定位和移动网络技术的不断发展以及智能设备的普及应用，Web上出现了大量包含位置信息和文本信息的空间-文本对象（后文简称空间对象），进而使得基于位置的服务（location based service，LBS）得到了广泛应用。近年来，有学者提出以一组空间对象作为空间关键字查询结果的基本单元，这组空间对象的特征联合起来以满足用户的查询需求，这种查询方法称为集合空间关键字查询（collective spatial keyword query，CSKQ）[1-5]，该类方法在空间数据库查询领域逐渐受到关注。CSKQ的基本思想是，给定一个空间关键字查询条件（包括查询位置和查询关键字），以最小的代价查找一组对象，该组对象需要满足如下3个基本条件：（1）能够覆盖所有查询关键字；（2）组内对象与查询位置接近；（3）组内对象之间位置相互接近。虽然目前已有一些CSKQ方法，但这些方法存在以下不足：（1）查询结果仅提供一组空间对象，但实际应用中返回top-k组对象可为用户提供更多的选择；（2）没有考虑组内空间对象之间的关联访问程度，而在现实中位置临近的不同类型对象之间通常具有密切的关联访问关系，例如旅游景点与其周边的酒店和餐厅经常被用户关联访问，关联访问度越大，用户越有可能同时访问这些对象，得到的结果也越符合用户的需求；（3）集合空间关键字精确查询往往需要枚举目标数据集中所有对象的所有可能组合，这将导致计算量非常庞大，进而影响查询响应速度。针对上述问题，本文提出一种新的集合空间关键字近似查询方法，称为Top-k集合空间关键字近似查询（Top-kcollective spatial keyword approximate query，Top-kCSKAQ）方法。

下面结合具体例子说明本文方法的基本思想。

例1图1给出了8个空间对象{O1,O2,…,O8}及它们的描述信息，表1给出了它们的位置信息，表2是用户历史访问记录，根据用户历史访问记录可以挖掘出空间对象之间的关联访问度。假设某个游客在位置〈5，4〉处提出查询关键字“Shopping，Restaurant，Hotel”。传统集合空间关键字查询方法返回的top-1结果为{O3,O8,O7}，top-2结果为{{O3,O8,O7},{O6,O2,O8}}。但如果在考虑距离的同时考虑组内对象的关联访问度，即利用本文提出的Top-kCSKAQ方法，则返回的top-1结果为{O6,O2,O8}，top-2结果为{{O6,O2,O8},{O3,O8,O7}}。这是因为根据历史用户访问记录，可以观察到O6,O2,O8被关联访问的可能性更大。

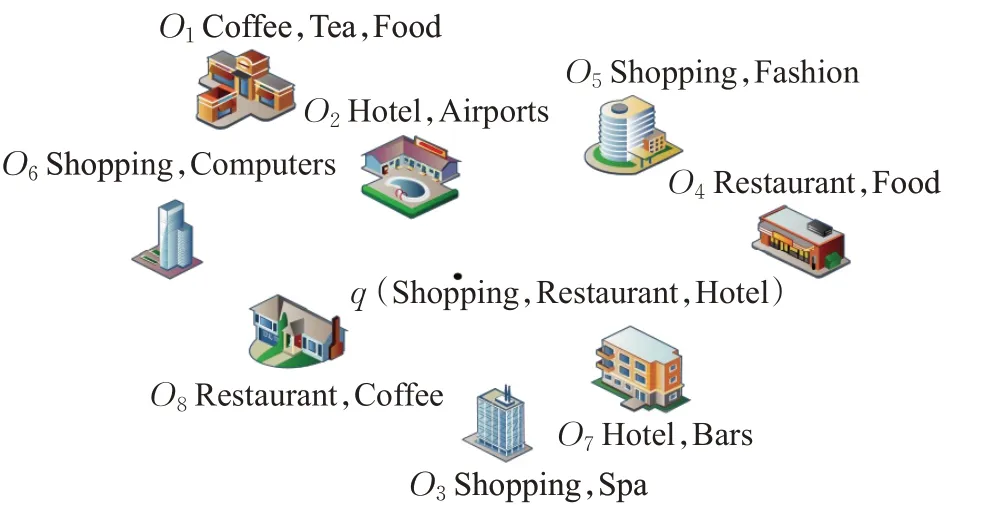
图1 空间对象及其文本描述Fig.1 Spatial objects and their textual descriptions

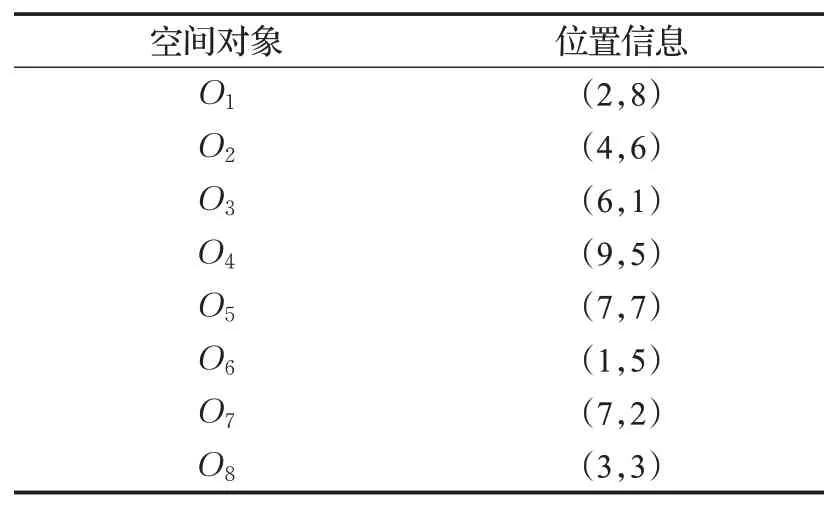
表1 空间对象的位置信息Table 1 Location information of spatial objects

表2 空间对象的用户历史访问记录Table 2 User check-in records for spatial objects

本文的贡献总结如下：

（1）提出了基于Apriori算法的空间对象关联访问度评估方法。

（2）设计了一种新的候选空间对象组合评分函数，据此对候选对象组合进行排序，选取top-k组近似结果。

（3）提出了一种基于VP-Tree的剪枝策略，实现快速邻域匹配，修剪空间对象，减少计算量。

（4）在Yelp真实数据集进行了大量的实验，评估Top-kCSKAQ方法的效率和有效性。

1 相关工作

1.1 空间关键字查询

传统的空间关键字查询将查询位置和查询关键字作为参数，并返回与这些参数在空间和文本上相关的空间对象。文献[6-27]在研究空间-文本查询的不同方面做出了一系列的贡献。传统的空间关键字查询主要考虑空间相近性和文本相似性，忽略了用户偏好和语义近似等方面。针对该问题，文献[6-9]研究了空间关键字语义查询方法，目标是找到在空间邻近性、文本相似性和语义相关性方面最优的对象。文献[4]在空间关键字查询中考虑了用户偏好，更好地满足用户的个性化需求。已有的研究大多数集中在欧式空间中如何有效处理空间关键字查询，但事实上人们的日常生活是被路网约束的，空间邻近性应该由最短路径距离而不是欧氏距离来决定，在欧式空间查询的最优结果在实际中不一定是最优的结果。所以现在一些工作研究了一个新的问题，即在路网上进行空间关键字查询[11-13]。与欧式空间相比，基于路网的空间关键字查询的研究更具有现实意义和价值，也给研究者们带来了更大的挑战。同时一些方法研究路线规划查询[14-16]，旨在找到满足用户需求的最优路线，比如可以利用基于关键字的最优路线查询为用户规划包含用户所有感兴趣的旅游景点并且花费较低的一条路线。有一些研究者们没有考虑上述内容，而是关注于社交网络中的查询。比如，文献[1]提出了一个社会空间组查询，该查询选择一组附近的具有紧密社交关系的参与者。要求与会者到集合点的空间距离最小，同时满足一定的社会约束。

1.2 集合空间关键字查询

通常情况下，只通过单个空间对象很难满足用户的所有查询需求，所以进而提出集合空间关键字查询方法。在文献[28-29]中，提出了一种新的空间关键字查询，称为m-最近邻关键字（mCK）查询，其目的是找到与m个用户指定关键字匹配的空间最近邻元组。Cao等人[2-3]提出了集合空间关键字查询问题（collective spatial keyword query problem，CoSKQ），即检索所有对象中包含的关键字共同覆盖查询关键字的一组对象。文献[3]提出高效处理空间关键字组查询，解决了三个实例化的检索top-k组的问题，设计了精确解和具有可证明的近似解，并研究合并对象权重的问题的加权版本。文献[4]提出新的个性化空间关键字查询问题-集合关键字偏好查询（collective keywords preference query，CKPQ），设计了基于访问历史和潜在POIs主题的用户偏好模型，然后根据集合内空间对象之间的最大距离、集合内空间对象到查询位置的最大距离以及集合的可达性（由POI流行度和拥塞度确定，避免在高峰时间访问受欢迎的POI）构造一个成本函数，根据该模型计算候选群体的成本，检索一组结果。文献[30]目的是检索可以覆盖所有查询关键字，组内对象接近查询位置，组内对象距离最小的top-k组对象。文献[5]定义了反向集合空间关键字查询（reverse collective spatial keyword query，RCSKQ）。它是一种新颖的反向空间关键字查询，用于查找CSKQ中包含查询对象的所有用户。提出了两种新的过滤策略，一种是利用改进的G-Tree索引结构（具有最大距离的反向G-Tree，G-Tree是一种改善最短路径问题计算性能的路网指标结构）来解决计算开销问题的用户过滤策略。另一种是无索引结构的启发式过滤，减少搜索空间。值得一提的是，以往的工作仅针对欧式空间中的集合空间关键字查询问题，Gao等人[31]、Su等人[32]研究了路网上的空间关键词集合查询处理问题。

综上可见，空间关键字查询方法的研究已经从多个方面展开，上述方法重点在于查找单个空间对象作为结果，现有的集合空间关键字方法也大多仅根据距离关系检索结果。然而，上述集合空间关键字查询方法忽略了空间对象之间的关联关系，这可能使查询结果不能让用户满意。针对上述问题，本文综合考虑了距离和空间对象之间的关联访问度，提出了关联访问度的评估方法，设计了一种新的评分函数，用来度量组合的得分。在此基础上，提出了一种基于VP-Tree的剪枝策略，以提高索引速度。

2 相关工作问题定义和总体解决方案

2.1 问题定义

定义1（Top-k集合空间关键字查询-TkCoSKQ[2-3，33-35]）给定空间对象集合D，空间关键字查询q，包含查询位置q.l，一组查询关键字q.w和k值，TkCoSKQ返回top-k组空间对象和每组对象的最大综合距离，最大综合距离由该方法提出的评分函数决定，计算方法如式（1）所示：

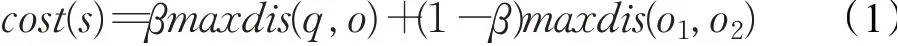
其中，β为调节参数，maxdis(q,o)表示组内空间对象到q的最大距离，maxdis(o1,o2)表示组内任意两个空间对象之间的最大距离，cost(s)是候选对象组合s的最大综合距离。

定义2（Top-kCSKAQ）给定空间对象集合D，用户历史访问记录R，空间关键字查询q，包含查询位置q.l，一组查询关键字q.w和k值，Top-kCSKAQ返回综合距离最小的top-k组空间对象，综合距离由评分函数决定。

定义3（关联访问度）给定空间对象集合D和用户历史访问记录R，D中的某组对象经常被用户共同访问的次数越高，则该组对象的关联访问度越高。

定义4（评分函数）给定一组空间对象，其综合距离评分函数包含距离和关联访问度两个部分，计算方法如式（2）所示：

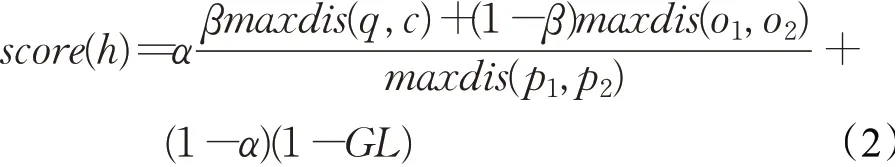
其中，h是候选空间对象组合；α为调节参数，用于平衡距离和关联访问度在评分函数中的作用；maxdis(p1,p2)是空间对象数据集中任意两个对象之间的最大欧式距离，GL是该组空间对象之间的关联访问度，maxdis(q,c)表示组内空间对象到q的最大欧式距离，maxdis(o1,o2)表示组内任意两个空间对象之间的最大欧式距离。maxdis(q,c)+maxdis(o1,o2)表示评分函数中的距离部分，记作距离分数，并对其进行归一化处理。β是调节参数，用于平衡组内空间对象到q的最大欧式距离和组内任意两个空间对象之间的最大欧式距离在距离分数中的作用，本文只考虑β=0.5的情况。

定义5（局部邻域）对于给定空间对象集合D及其子集Z，Z⊆D以及邻域阈值σ，Z的σ-局部邻域定义为：

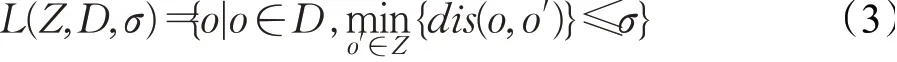
该集合由D中包含的对象与Z中至少一个对象的距离不超过阈值σ的对象构成。

2.2 解决方案

本文的总体解决方案如图2所示，共分3步。

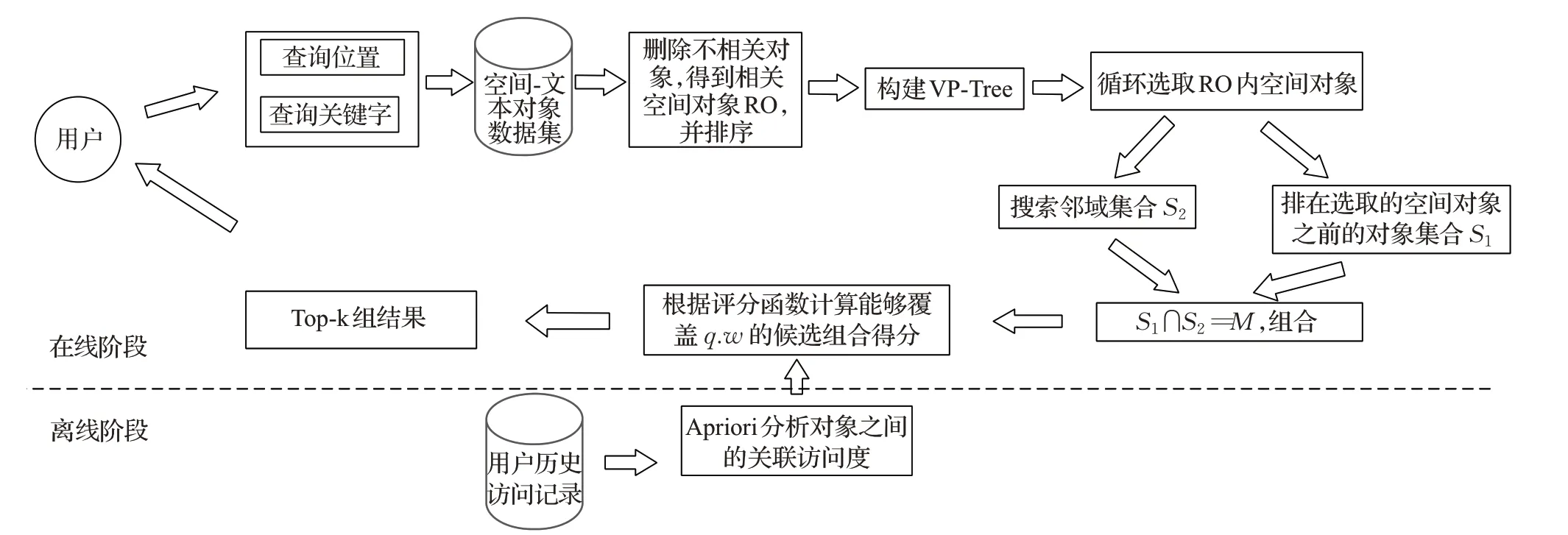
图2 解决方案总体框架图Fig.2 Overall solution framework

步骤1数据处理。给定查询条件，包含查询位置和一组查询关键字，删除不包含任何查询关键字的空间对象，将剩余的空间对象记作相关空间对象，根据到查询点的欧式距离对其进行升序排序。

步骤2剪枝。循环选取相关空间对象，利用VPTree加速搜索每次选取的空间对象的局部邻域，修剪数据集中的空间对象，只保留邻域内的空间对象，并将每次选取的空间对象之前的对象取出与局部邻域做交集，然后对交集内的空间对象进行组合。

步骤3计算空间对象组合的得分，返回top-k组结果。该步骤分为在线和离线处理两个阶段，离线处理阶段利用Apriori算法对空间对象进行关联分析，计算空间对象之间的关联访问度。在线处理阶段将能够覆盖所有查询关键字的空间对象组合作为候选组合，并根据评分函数计算其得分，将得分最小（即综合距离最小）的前k个候选组合作为最终的top-k组结果。

3 Top-k组查询结果的精确选取算法

本章主要阐述如何对空间对象之间的关联访问度进行评估，提出一种top-k组结果的精确选取算法，并给出精确选取算法的实现过程。

3.1 空间对象之间的关联访问度评估

Apriori算法使用逐层搜索的迭代方法，其中k项集用于探索(k+1)项集。首先，通过扫描数据库，求出每个项的计数，得到满足最小支持度的项，找出频繁1项集的集合，记为L1。然后，使用L1找出频繁2项集的集合L2，使用L2找出L3，以此类推，直到不能再找到频繁k项集。在该过程中使用频繁项集的先验性质来压缩搜索空间，即频繁项集的所有非空子集也一定是频繁的。找出满足最小支持度的项集后，可通过计算得到满足最小置信度的强关联规则，最小置信度和最小支持度可以根据需求设置。给定空间对象集合D和用户对空间对象的历史访问记录R，Apriori算法可以从大量的用户历史访问记录中发现空间对象之间潜在的关联。

本文引言部分的图1、表1和表2分别给出空间对象和用户历史访问记录。假设对O2，O6进行关联度分析，O6的支持度为1/4；O2的支持度为1/2；O2∩O6的支持度为1/8；关联度为GL(O6|O2)=1/8/1/2=0.25，这表明访问过O2的用户中有25%的用户会访问O6。算法1给出了利用Apriori算法对空间对象进行关联访问度分析的执行过程。

算法1基于Apriori的空间对象关联访问度分析算法

Apriori算法首先扫描一遍数据集，从中生成一项集C1，然后扫描C1，过滤不满足最小支持度的项集，得到频繁1项集L1（第1行）。根据Apriori原理，非频繁项集的所有超集也都是非频繁的，因此，第二轮迭代中，只需要对上一轮迭代产生的频繁项集进行新的组合即可。然后，检查新的组合是否满足最小支持度要求，将不满足的新组合给过滤，直到没有新组合可生成为止（第2～18行）。调用aprioriGen函数，通过频繁项集Lk-1生成无重复项集Ck（即项数为k的项集）（第3行）。接下来，迭代扫描R并进行候选计数（第4～9行），过滤掉不满足条件的组合，返回项集中不小于最小支持度的项集作为频繁k项集Lk（项数为k的频繁项集）（第10行），集合L包含所有频繁项集（第12行）。最后，循环选取L中的每一个频繁项集，为其计算置信度conf（第14行），并判断conf是否不小于最小置信度minConf，如果conf≥minConf，将该项集作为一个关联分析结果，加入到关联规则集合RL中（第15～17行）。重复执行上述过程，直到所有频繁项集都被访问过为止，返回关联规则RL（第19行）。

3.2 Top-k组结果精确选取算法（简称CSKAQ-E）

在本节中，提出一种准确选取算法，记作CSKAQE，查找覆盖所有查询关键字的空间对象组合，根据评分函数计算每个候选组合的综合距离得分，并选择得分最低的top-k组对象作为查询结果。CSKAQ-E算法的执行过程如图3所示。

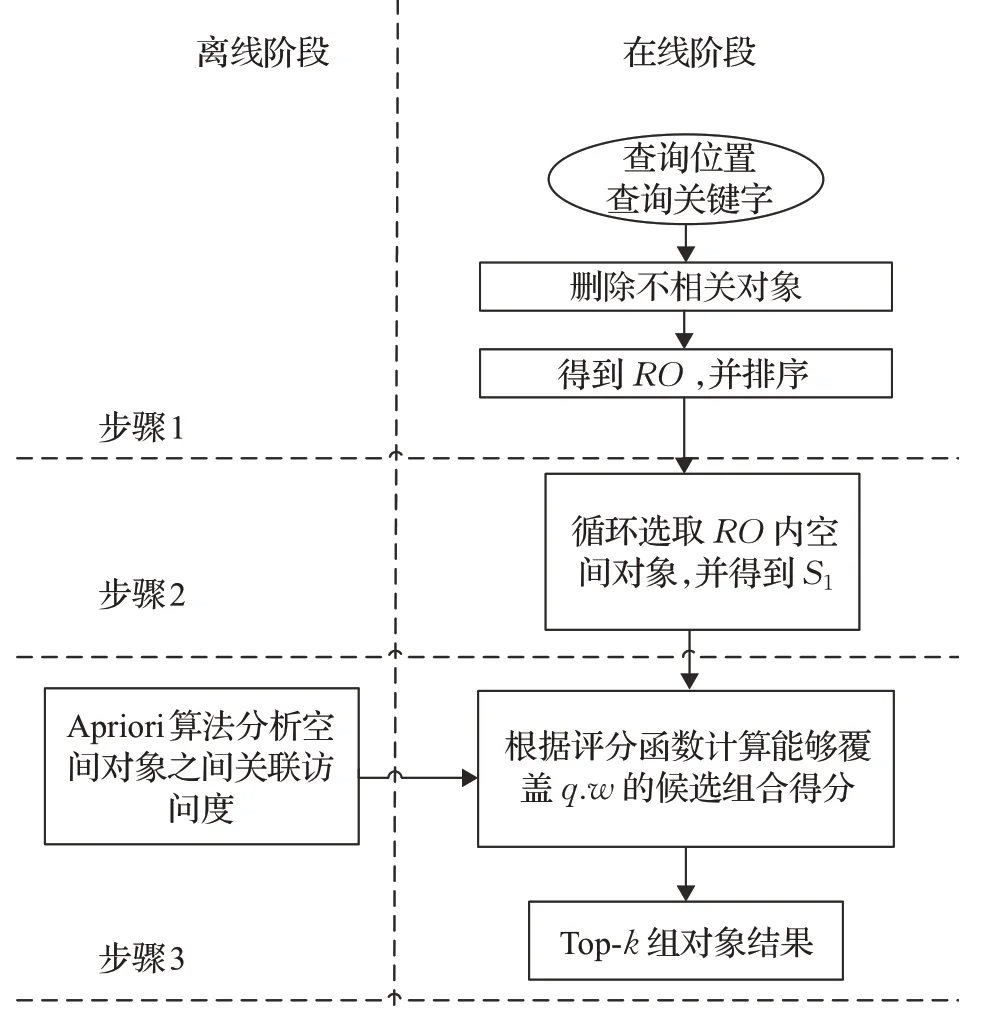
图3 CSKAQ-E执行过程Fig.3 CSKAQ-E execution process

CSKAQ-E算法首先删除空间对象集合D中不包含任何查询关键字的对象，只保留与查询关键字相关的对象作为相关空间对象集合RO；根据到查询q的距离对RO中的对象进行升序排序（第1行）。以顺序循环方式逐个选取RO中空间对象，被选取的对象记为c（第3行），然后将与查询q的距离小于c到q的距离的空间对象加入集合S1（第7行），这种情况下，c到q的距离则为组内空间对象到查询q的最大距离。在此基础上，将S1中的对象进行组合(o1,o2)（第8行），并将这些组合根据距离进行升序排序。接下来，根据组合排序结果顺序循环选取组合，每次选取一对组合，记为x={c,o1,o2}（第10行），若x能够覆盖所有查询关键字，则将该空间对象组合视为候选空间对象组合h，并利用式（2）计算h的得分score(h)（第11～18行）。最后，检查结果集J的大小是否小于k，当结果集中的空间对象组合的数量小于k时，直接将h加入到结果集J中，得到J中组合的最大得分Jmaxc（第19～23行）；当结果集数量为k，并且候选组合得分小于Jmaxc时，将该组合插入到J中，并将J中得分最大的组合删除，更新Jmaxc（第24～26行），直到所有的组合都被访问过为止。重复上述过程，直到结果集|J|＞k，并且选取的空间对象到查询点的距离大于Jmaxc，停止迭代，输出结果集J。

算法2 Top-k组结果精确选取算法CSKAQ-E

例2利用表1、表2和图1中的信息，给定查询位置〈5，4〉、查询关键字为“Shopping，Restaurant，Hotel”。根据上述查询条件，首先删除表1所示空间对象集合中的不相关对象O1，得到相关对象集合RO，并对其进行升序排序，排序结果为：RO={O2,O8,O7,O3,O5,O4,O6}。CSKAQ-E算法获得top-3结果的处理过程分析如下：

首先，根据上述RO中的排序结果，以顺序循环选取方式，每次从RO中选取一个空间对象，记作c。第一次选取O2，即c=O2，然后从RO中计算与查询q的距离小于c到q的距离的空间对象集合S1，S1={O2}，但此时没有与之组合的空间对象。第二次选取，c=O8，得到S1={O8,O2}，将S1中保护的空间对象进行组合，可以得到(o1,o2)=(O8,O2)。算法CSKAQ-E第10行需得到空间对象组合x={c,o1,o2}，但此时x={O8,O2}，可判断出x包含的对象不能覆盖所有查询关键字，因此没有候选对象组合。同理，当c=O7时，所产生的空间对象组合也不能覆盖所有查询关键字，也没有候选空间对象组合。c=O3时，S1={O2,O8,O7,O3}，其中的对象形成的组合包括(o1,o2)={(O3,O7),(O8,O2),(O3,O8),(O7,O8),(O7,O2),(O3,O2)}，此时，所有空间对象组合为x={{O3,O7},{O3,O8,O2},{O3,O8},{O3,O7,O8}，{O3,O7,O2},{O3,O2}}，由此可见，空间对象组合{O3,O8,O2},{O3,O7,O8}能够覆盖查询关键字，因此将这两组对象作为候选对象组合h，即h={{O3,O8,O2},{O3,O7,O8}}。

接下来，根据式（2）的评价函数计算候选对象组合的排序得分，其中候选空间对象组合h内空间对象之间的关联访问度是由Apriori算法获得的关联规则RL得到，score({O3,O8,O2})=0.849,score({O3,O7,O8})=0.933。结果集J中的空间对象组合的数量小于3，直接将{O3,O8,O2}加入J，更新Jmaxc=0.849。然后，将{O3,O7,O8}加入到结果集J中，并更新Jmaxc=0.933。当结果集数量为3，并且候选组合得分小于Jmaxc时，将该组合插入到J中，并将J中得分最大的组合删除，更新Jmaxc，直到所有的候选组合都被访问过。重复上述过程，直到结果集|J|＞k，并且选取的空间对象到查询点的距离大于Jmaxc。将J中空间对象组合根据得分升序排序，最终CSKAQ-E算法得到的top-3结果为{{O4,O7,O3},{O6,O8,O2},{O3,O8,O2}}。

3.3 时间复杂度分析

CSKAQ-E方法的时间复杂度为O(ms(|q.w||RO|+|h|+k))

分析：算法2中首先假设对RO中空间对象进行的迭代次数为m(m≤|RO|)，对S1内空间对象进行任意组合，得到组合(o1,o2)，假设S1内的(o1,o2)组合个数记作s。然后，判断空间对象组合x是否能覆盖所有查询关键字q.w的时间复杂度是O(|q.w||RO|)，其中|q.w|代表查询关键字个数。接下来，计算候选空间对象组合h的得分score(h),需从关联规则RL中查找h内空间对象的关联访问度，查找h中所有组合的关联访问度的时间复杂度为O(|h|)，|h|代表集合h中的空间对象组合个数。最后，再将候选空间对象组合插入到J中，并将J中得分最大的组合删除，更新Jmaxc的时间复杂度为O(k)，k表示指定的结果个数。综上，CSKAQ-E算法的时间复杂度为O(ms(|q.w||RO|+|h|+k))。

需要指出的是，由于这种方法需要将所有包含查询关键字的空间对象互相组合，并且计算所有候选组合的得分，算法复杂度高，计算量大，查询效率较低。因此，需要设计一种近似查询匹配方法，在确保准确性的情况下提高执行效率。

4 Top-k组查询结果的近似选取算法

本章提出一种基于VP-tree的剪枝策略，在此基础上提出一种top-k近似查询匹配算法。

4.1 VP-Tree结构

VP-Tree[36]是一种二元空间划分树，其基本思想是选取某个空间对象作为制高点，然后计算其他对象到制高点的距离，并根据距离对空间对象数据集进行划分。利用VP-Tree可快速进行给定空间对象的近邻查询和范围查询。

对于给定的相关空间对象集合RO，VP-Tree从根节点以自顶向下方式构建，构建时需选取制高点，指定一个距离函数和一个阈值。首先根据文献[36]的思想，在RO中随机抽样选取一组对象作为候选制高点，利用剩下的对象对其进行评估，最终选取能够构建出高度平衡的VP-Tree的对象作为制高点。然后以该制高点作为依据，将数据集中与制高点的欧式距离不高于给定阈值的对象划分到左子树，与制高点的欧式距离高于给定阈值的对象划分到右子树。左右子树以递归方式再进行划分，直到节点仅包含一个对象（即叶子节点）。VPTree的构造时间复杂度是O(|RO|lg|RO|)。

图4给出了构建VP-Tree的实例。假设选取点＜5，6＞为制高点，分别计算其余四个对象到制高点的欧式距离，将距离制高点小于给定阈值（设为4）的对象划分到左子树。

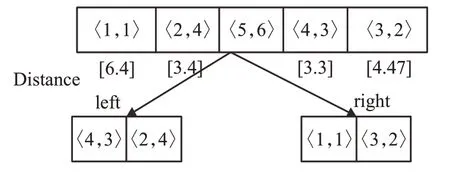
图4 VP-Tree例子Fig.4 Example of VP-Tree

4.2 局部邻域搜索

给定邻域阈值σ，对于空间对象数据集中的任一对象r∈RO，根据式（3）计算可得到{r}的σ-局部邻域L({r},D,σ)，但为每个空间对象都计算其σ-局部邻域耗时较长，因此为了提高空间对象的σ-局部邻域搜索的效率，本文使用VP-Tree加速对空间对象的σ-局部邻域搜索。

给定相关空间对象集合RO中一个对象，利用VP-Tree搜索该对象的σ-局部邻域的过程为：自顶向下比较VP-Tree中各节点与给定对象之间的欧式距离，如果VP-Tree中某个中间节点在该对象的σ-局部邻域中，那么该节点的所有后继对象都在该对象的局部邻域当中。理想情况下，VP-tree搜索的时间复杂度是O(lg|RO|)。由此可见，利用VP-Tree，可以快速得到与给定空间对象位置接近的其他空间对象，从而为快速获取top-k组对象提供了支持。

4.3 Top-k组结果近似选取算法（简称CSKAQ-A）

本节提出一种基于剪枝策略的CSKAQ-A方法，该方法通过VP-Tree需要搜索每个空间对象的局部邻域，修剪空间对象，进而只保留邻域内的空间对象，减少组合可能性和计算量，最后选择综合距离最低的top-k组作为近似查询结果。CSKAQ-A算法的执行过程如图5所示。

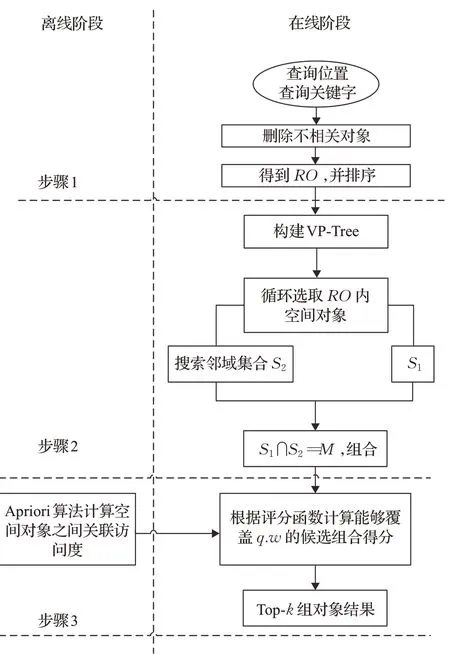
图5 CSKAQ-A执行过程Fig.5 CSKAQ-A execution process

CSKAQ-A算法首先删除空间对象集合D中不包含任何查询关键字的空间对象，只保留与查询关键字相关的空间对象作为相关空间对象集合RO；根据到查询q的距离对RO中的空间对象进行升序排序（第1行）。然后，对J、h、x、Jmaxc等进行初始化，并将相关空间对象集合RO构建成VP-Tree（第2行）。接下来，将与查询q的距离小于c到q的距离的空间对象加入集合S1（第7行），并利用VP-Tree对每次选取的对象c进行局部邻域搜索，得到c的σ-局部邻域集合S2（第8行），在此基础上计算S1∩S2=M，并对M进行升序排序（第9～10行），这种情况下，c到q的距离则为组内空间对象到查询q的最大距离，该策略可以避免重复计算。然后，对M内空间对象进行任意组合，得到组合(o1,o2)，后续步骤与CSKAQ-E方法相同。

算法3 Top-k组对象近似选取算法CSKAQ-A

利用S1∩S2=M，减少组合可能性和计算量，可以避免重复计算。

分析：c的σ-局部邻域是L({c},RO,σ)，近似算法CSKAQ-A仅保留距离c较近的空间对象，可减少可组合的空间对象数量，进而减少计算量。假设c1是c的σ-局部邻域L({c},RO,σ)内的空间对象，利用VP-Tree搜索c1的σ-局部邻域集合L({c1},RO,σ)。将L({c},RO,σ)内的空间对象进行任意组合，再循环选取组合，将其与c共同形成空间对象组合，此时c和c1将进行一次组合。当循环选取相关空间对象到c的局部邻域内的对象c1时，L({c1},RO,σ)内将包含c，然后将c1与其邻域内的任意对象的组合形成空间对象组合，此时c和c1将可能出现重复组合。通过计算S1∩S2=M可以避免该情况，因为根据S1集合的特性，S1集合包含到q的距离小于c到q的距离的空间对象，L({c},RO,σ)内的对象c1到q的距离若大于c到q的距离，则它不会出现在c的M集合中，并且当循环选取到c的局部邻域内空间对象c1时，c则会出现在c1的M集合中，此时c与其局部邻域内的对象只需要组合和计算一次，可避免重复计算。

例3利用表1、表2和图1中的信息，给定查询位置〈5，4〉、查询关键字为“Shopping，Restaurant，Hotel”。根据上述查询条件，首先删除表1所示空间对象集合中的不相关对象O1，得到相关对象集合RO，并对其进行升序排序，排序结果为RO={O2,O8,O7,O3,O5,O4,O6}。CSKAQ-A算法获得top-3结果的处理过程分析如下：

对于得到的相关对象集合RO={O2,O8,O7,O3,O5,O4,O6}，CSKAQ-A算法先将RO中的空间对象构建成VP-Tree，然后根据顺序循环方式，每次选取RO中的一个空间对象，记作c。与CSKAQ-E算法相比，CSKAQ-A算法除了获取与q的距离小于c到q的距离的空间对象集合S1，还利用VP-Tree加速c的σ-局部邻域搜索，得到c的σ-局部邻域集合S2，并做S1∩S2=M操作，在此基础上对M内的空间对象进行组合，也就是组合(o1,o2)从集合M中获得，该策略能够使得距离c较远的空间对象被剪枝，进而|(o1,o2)|的数量大大减少。

根据前述讨论，c=O2、O8、O7的情况下没有产生候选对象组合。当c=O3时，S1={O2,O8,O7,O3}，利用VP-tree可获得c的σ-局部邻域为S2={O8,O7,O3}，S1∩S2=M={O8,O7,O3}，此时可能的组合有(o1,o2)={(O3,O7),(O3,O8),(O7,O8)}，即空间对象组合为x={{O3,O7},{O3,O8},{O3,O7,O8}}，据此可判断{O3,O7,O8}能够覆盖查询关键字，因此将其作为候选对象组合h，即，h={{O3,O7,O8}}，score({O3,O7,O8})=0.933。结果集J中的空间对象组合的数量小于3，将{O3,O7,O8}直接加入结果集J中，并更新Jmaxc=0.933；当结果集数量为3，并且候选组合得分小于Jmaxc时，将该组合插入到J中，并将J中得分最大的组合删除，更新Jmaxc，直到所有的候选组合都被访问过（该过程与CSKAQ-E算法相同）。重复上述过程，直到结果集|J|＞k，并且选取的空间对象到查询点的距离大于Jmaxc。将J中空间对象组合根据得分升序排序，最终CSKAQ-A算法得到的top-3结果为{{O6,O8,O2},{O3,O7,O8},{O4,O7,O5}}。

4.4 时间复杂度分析

CSKAQ-A方法的时间复杂度为O(|RO|lg|RO|+m(lg|RO|+|S1||S2|+ss(|q.w||RO|+|h|+k)))

分析：算法3首先对相关空间对象集合RO构建VP-Tree的时间复杂度为O(|RO|lg|RO|)，然后利用VPTree对选取的对象c进行局部邻域搜索，获得集合S2的时间复杂度为O(lg|RO|)，S1∩S2=M的时间复杂度为O(|S1||S2|)。然后对M内空间对象进行任意组合，得到组合(o1,o2)，令(o1,o2)组合个数记作ss。接下来，判断空间对象组合x是否能覆盖所有查询关键字q.w的时间复杂度是O(|q.w||RO|)。计算候选空间对象组合h的得分score(h)，需从关联规则RL中查找h内空间对象关联访问度，查找h中所有组合的关联访问度的时间复杂度为O(|h|)，|h|代表集合h中的空间对象组合个数。最后，再将该组合插入到J中，并将J中得分最大的组合删除，更新Jmaxc的更新阶段时间复杂度为O(k)，k表示指定的结果个数。综上，CSKAQ-A算法的时间复杂度为O(|RO|lg|RO|+m(lg|RO|+|S1||S2|+ss(|q.w||RO|+|h|+k)))，其中m为对RO中空间对象进行的迭代次数(m≤|RO|)。

综上可见，相比于CSKAQ-E算法，CSKAQ-A算法中|(o1,o2)|,|x|,|h|数量均减少，因此计算量减小，查询速度加快。

5 实验

5.1 数据和实验设置

5.1.1 数据

实验测试数据采用Yelp数据集，Yelp包含了20 290个空间对象，74 773条用户评论，每个空间对象都包含ID、名称、经纬度和类别等属性，每条评论数据集都包含用户ID、空间对象ID和评论内容。

5.1.2 参数设置

表3给出了本文算法的参数默认值。在实验过程中，通过改变一个参数的值、固定其他参数的值来讨论该参数对实验结果的影响。所有实验都采用Java实现，电脑配置为主频3.7 GHz的CPU，32.0 GB内存，Windows10操作系统。

表3 参数的默认值Table 3 Default values for parameters

5.1.3 算法对比

将本文提出的精确选取方法（CSKAQ-E）和近似选取方法（CSKAQ-A）分别与文献[30]提出的TkCoSKQ方法中的RC算法（记作TkCoSKQ-RC）和最新的相关研究工作文献[4]提出的CKPQ中的RKD-Search算法（记作CKPQ-RKD-Search）进行对比。

TkCoSKQ-RC的基本思想是，选取候选组合时，对任意空间对象的组合，计算其欧式距离并设置上下边界条件，修剪不满足条件的组合，减少组合的可能性和计算量。最后将满足所有查询关键字的候选组合，根据评分函数计算其得分，返回得分（即综合距离）最小的top-k组结果。需要指出的是，在选取组对象时，该算法只考虑空间对象与查询位置之间的距离关系而没有考虑组内对象之间的关联访问度。

CKPQ-RKD-Search的基本思想是，针对每个查询关键字，都从查询区域中找到一个包含该查询关键字同时最接近查询位置的一个空间对象，然后将查找到的所有空间对象进行组合，根据评分函数计算该组合的综合得分。评分函数综合考虑了用户对空间对象的偏好程度、组内空间对象之间的最大距离、组内空间对象到查询位置的最大距离以及组内对象的可达性。

5.1.4 评价标准

本文设置5组空间关键字查询条件，针对每个查询条件，每个算法获取top-10组查询结果，进而每个算法最终得到50组查询结果，对每个算法获得的50组查询结果取平均测量结果。本文使用近似比[3，30]衡量查询效果，近似比的计算方法如下：

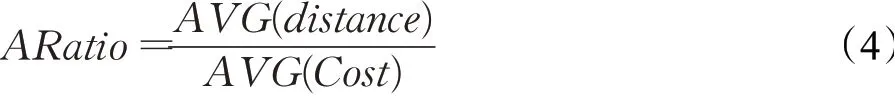
其中，AVG(distance)表示CSKAQ-E、CSKAQ-A和CKPQRKD-Search方法获得的距离分数的平均值；AVG(Cost)表示TkCoSKQ-RC获得的平均综合距离。近似比的结果等于或小于1，说明结果越好。

5.2 实验结果分析

本节主要研究在相同数据集上，表3中各参数分别对CKPQ-RKD-Search、TkCoSKQ-RC、CSKAQ-E和CSKAQ-A在查询效果和查询效率上的评估。

（1）结果集个数k值变化对查询效果和响应时间影响

将k的值分别设置为2～10。图6（a）显示了不同k值下各算法的查询响应时间。CSKAQ-E方法需要获取候选组合内空间对象之间的关联访问度，所以查询响应时间略大于TkCoSKQ-RC方法。CKPQ-RKD-Search方法在遍历索引结构时采用了剪枝策略，所以其查询响应时间要小于TkCoSKQ-RC和CSKAQ-E方法。CSKAQA方法每次对距离所选取的空间对象较远的空间对象进行修剪，减少组合的可能性和计算量，所以查询响应时间最短。在k值较小时，CSKAQ-E、CSKAQ-A以及CKPQ-RKD-Search方法的近似比结果要略大于1，因为相比TkCoSKQ-RC，CSKAQ-E和CSKAQ-A方法还考虑了组内空间对象之间的关联访问度。但随着k值增大，CSKAQ-A、CSKAQ-E的近似比结果越来越接近1，甚至CSKAQ-E方法要小于1，说明在所需查询结果增多时，CSKAQ-E方法的性能更好一些，也更符合用户的需求。CSKAQ-A方法始终略大于1，因为CSKAQ-A方法使用了修剪策略，生成的是近似查询结果。

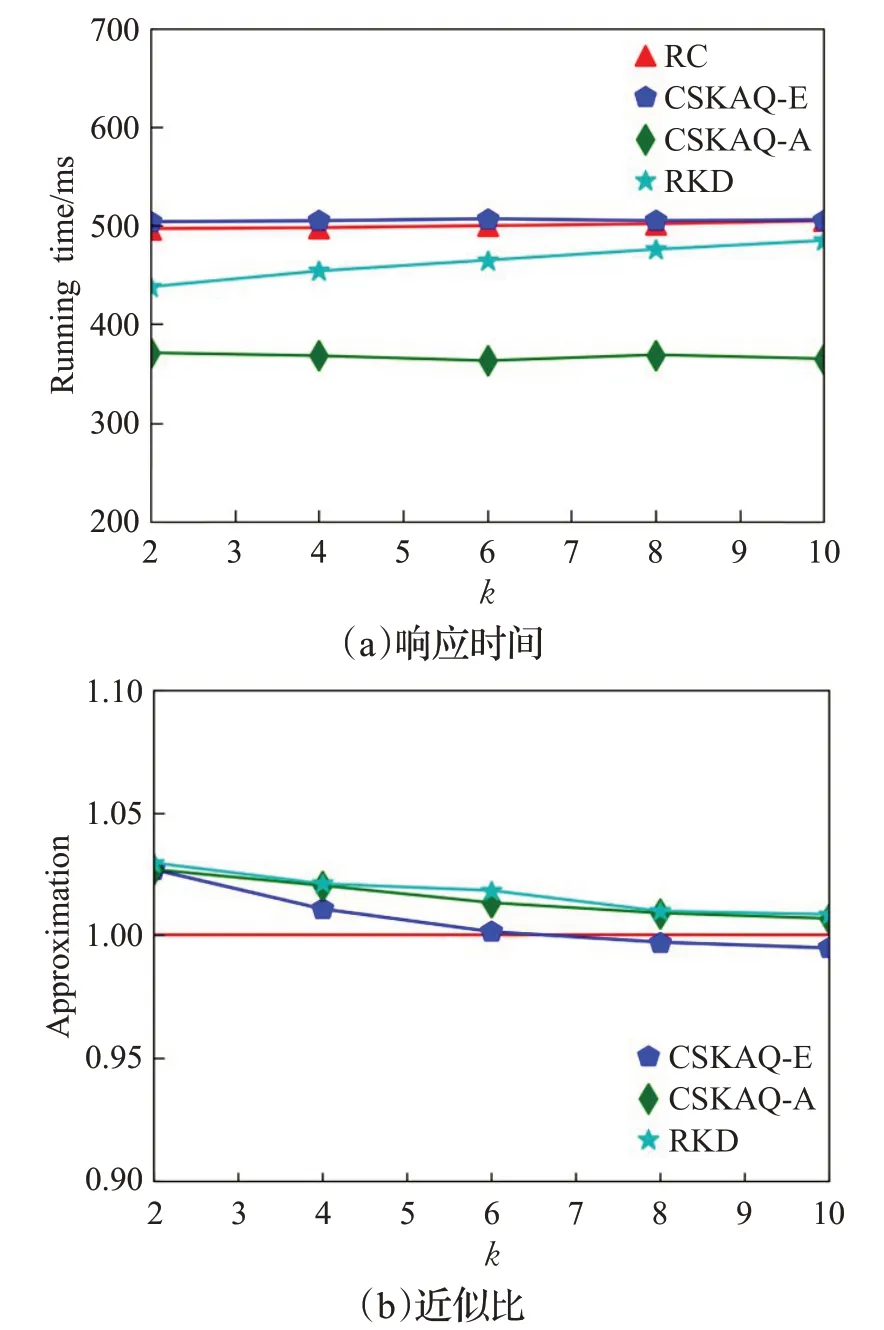
图6 k值变化对查询效果和响应时间的影响Fig.6 Effect of k value change on query effect and response time

（2）Keywords数量变化对查询效果和响应时间的影响

通过图7（a）给出了不同查询关键字数量情况下不同算法的查询响应时间变化情况。从图中可以观察到，四种方法的查询响应时间都会随着查询关键词的数量增加而增加，并且TkCoSKQ-RC和CSKAQ-E与CSKAQ-A的差距越来越大，因为查询关键字越多，需要计算的空间对象越多。CKPQ-RKD-Search和CSKAQ-A方法均采用了剪枝策略，因此查询相应时间较短。CKPQ-RKD-Search查询响应时间大于CSKAQ-A，是因为CKPQ-RKD-Search不仅考虑距离部分，还要计算用户偏好程度和组内对象的可达性；通过图7（b）还可以观察到，CSKAQ-A方法的近似比结果也仅略大于1，这说明本文近似方法在确保选取结果准确率的情况下，同时具有较高的执行效率。CSKAQ-E方法的距离分数要小于TkCoSKQ-RC，因为CSKAQ-E不仅考虑距离上的得分，还考虑组内空间对象的关联访问度，同时，TkCoSKQRC在考虑组合的上下边界条件时，一些较好的组合结果可能被剪枝掉。CSKAQ-A和CKPQ-RKD-Search方法近似比结果略大于1，因为它们均采用了剪枝策略，生成近似查询结果。

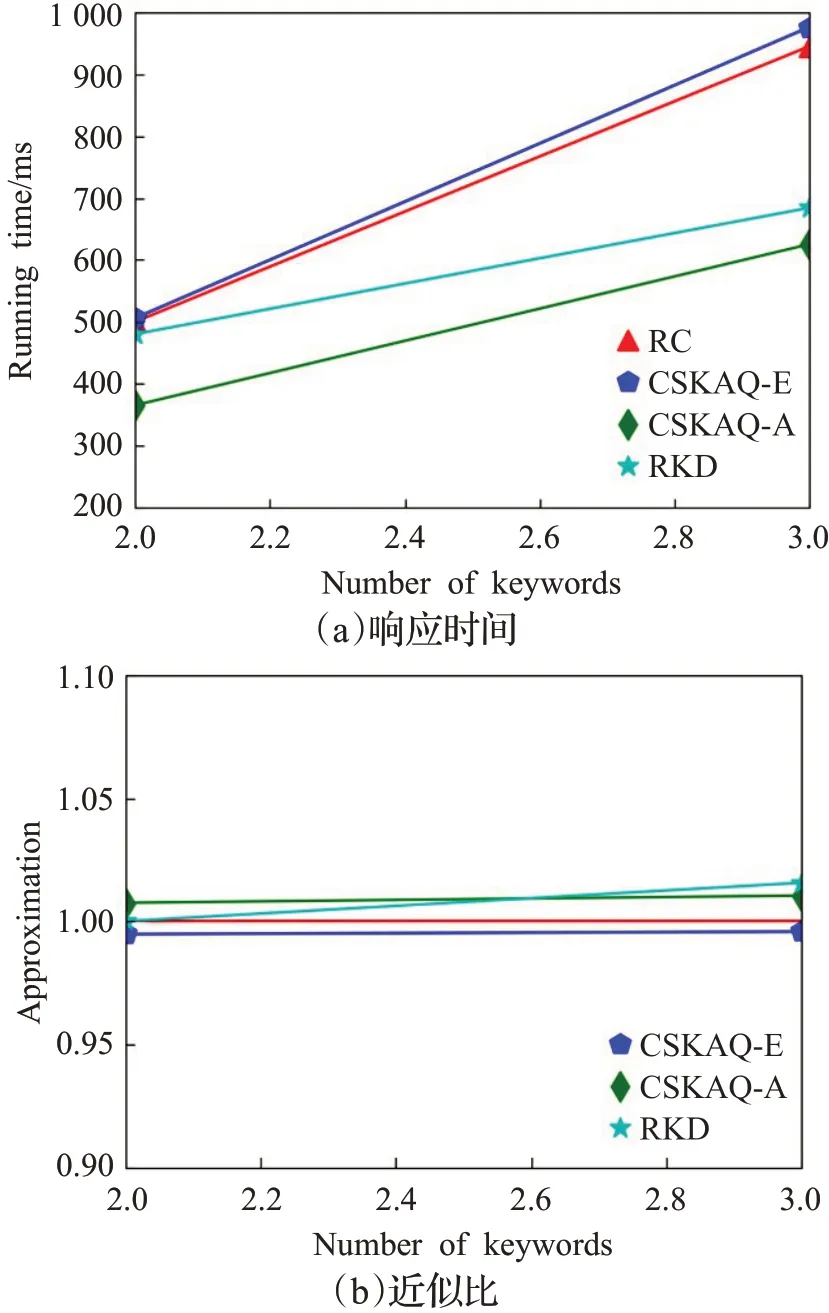
图7 Keywords数量变化对查询效果和响应时间的的影响Fig.7 Effect of change of number of keywords on query effect and response time

（3）|D|值变化对查询效果和响应时间的影响

通过图8可以观察到，随着数据集增大，四种方法的查询响应时间都随之增长，因为数据集越大，相关空间对象越多，计算量越大。数据集较小的情况下，TkCoSKQ-RC方法的查询响应时间最小，因为该方法不需要考虑组内空间对象之间的关联访问度，也不需要构建索引结构。但随着数据集的增大，CSKAQ-A方法的查询响应时间明显小于CSKAQ-E和TkCoSKQ-RC方法，并且差距也越来越大，同时也可以观察到CSKAQ-A方法的查询响应时间也小于CKPQ-RKD-Search方法。并且，随着数据集的增大，CSKAQ-E方法的近似比小于1，说明该方法的距离分数要小于TkCoSKQ-RC方法，CSKAQ-A方法得到的距离分数也仅略大于TkCoSKQRC。这说明本文提出的近似方法在结果准确率较高的情况下，同时具有较高的执行效率。

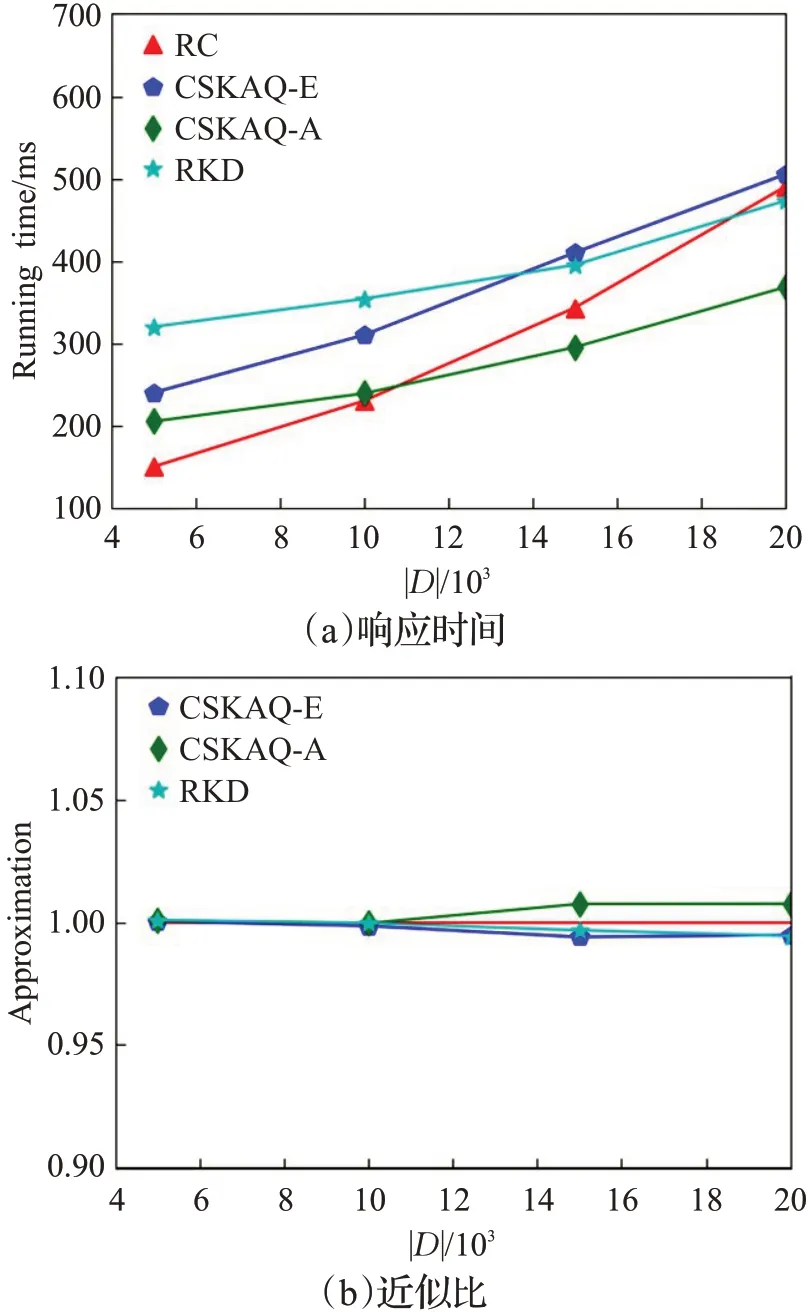
图8 数据集大小对查询效果和响应时间的影响Fig.8 Impact on query efficiceny and response time when dataset size varied

（4）阈值σ取值范围的影响

通过图9可以看到，随着σ的增大，CSKAQ-A方法查询响应时间越来越大，近似比逐渐减小。原因是随着σ增大，搜索到的局部邻域内的空间对象的数量增多，被剪枝的空间对象减少，组合的可能性变多，计算量变大，所以查询响应时间增大。但随着σ增大，查询效果得到了提升，查询到的结果更准确。

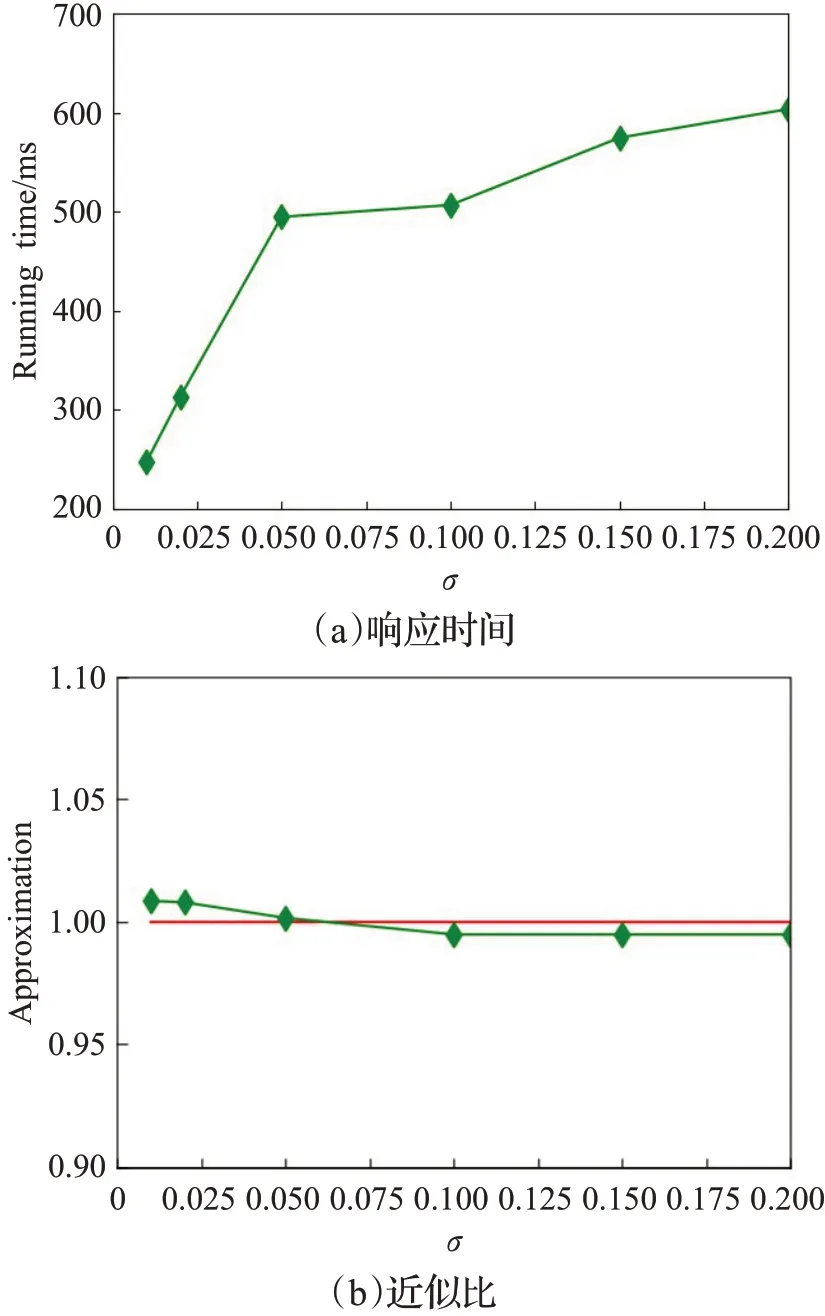
图9 阈值σ的影响Fig.9 Effect of threshold σ

（5）参数α值的变化对查询效果和响应时间的影响

从图10可以看出，α的变化对本文所提出的两种算法的查询响应时间几乎没影响。CSKAQ-A的响应时间明显小于CSKAQ-E方法，因为CSKAQ-A利用VPTree搜索空间对象的局部邻域，减少了相关空间对象，组合的可能性变少，计算量减小，查询响应时间小。通过图10（b）可以观察到，随着α的增大，CSKAQ-E方法的近似比结果小于1，得到的结果效果更好。

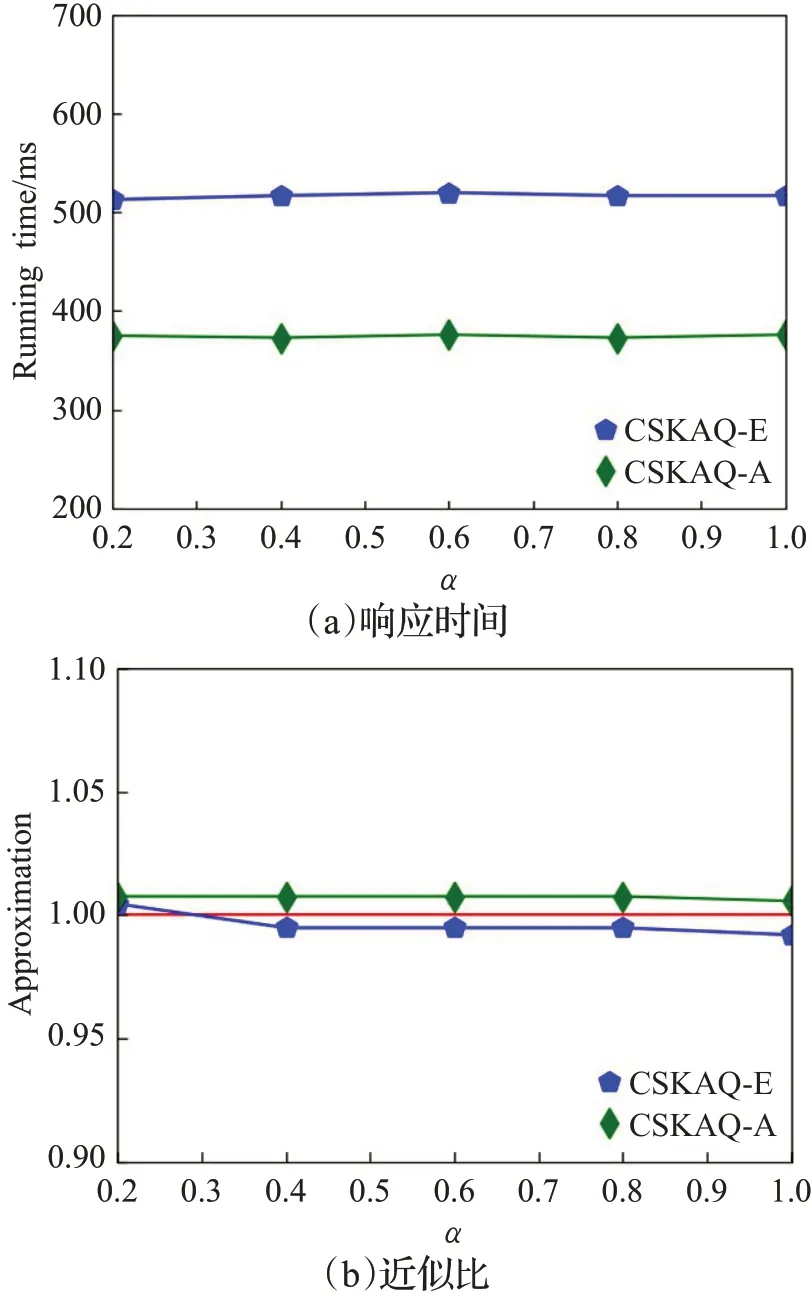
图10 参数α的影响Fig.10 Effect of parameter α value on query effect and response time

为了进一步验证本文所提出方法的查询效果，在50名用户中进行了以下实验。针对5组空间关键字查询条件Q1～Q5，各个方法均生成top-3结果。并让所有测试者对4个方法得到的查询结果进行投票，通过这50名用户的投票结果来衡量查询效果，图11展示其投票结果。由图11可以明显地观察出本文所提出的CSKAQ-A方法得到的查询结果，最受用户欢迎。相比其他两种方法，CSKAQ-E方法更受用户欢迎，所以本文提出的方法更能让用户满意。

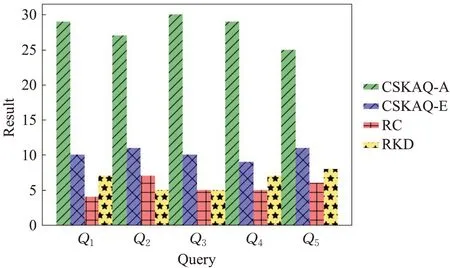
图11 用户投票结果Fig.11 User voting results

6 结束语

本文提出了一种新的集合空间关键字近似查询方法，记作Top-kCSKAQ，该方法研究了一种新的空间关键字查询问题，即空间对象之间的关联访问度，并通过Apriori算法对其进行评估。此外，提出基于VP-Tree的剪枝策略来优化解决方案，实现近似查询。最后在真实数据集中验证了本文所提出的算法的性能，同时实验结果表明，本文提出的算法不仅考虑是否能够覆盖所有查询关键字和组内空间对象到查询的距离以及组内空间对象之间的距离，还考虑了组内空间对象的关联访问度，这样的查询结果更符合用户的查询要求，并在一定程度上提高了用户的体验和满意度。但是查询到的一组对象可能会重复出现某个关键字，忽略了组内对象的多样性。因此未来工作中，在选取空间对象进行组合时，应该避免选取具有相同关键字的空间对象作为一组；或在最终选取查询结果时，考虑组内空间对象之间的多样性对结果排序的影响。