一种通用六阶紧致差分格式在耦合Schrödinger-KdV方程中的应用

仇佳栋,梁琪琪，胡志涛，韩丹夫

(杭州师范大学数学学院,浙江 杭州 311121)

非线性偏微分方程在量子力学、固体物理学、流体力学和等离子体物理学等许多学科中发挥着重要作用[1].为了描述以离子声速运动的坐标系中一维朗缪尔(Langmuir)和离子声波的非线性动力学，耦合Schrödinger-KdV(CSK)方程组[2-3]被提出.

考虑具有初始条件和周期性边界条件的一维CSK方程组[4]：

iεut+puxx-qvu-s|u|2u=0, (x,t)∈×(0,T],

vt+αvxxx+(βvm+ρ|u|2)x=0, (x,t)∈×(0,T],

u(x,t)=u(x+l,t),v(x,t)=v(x+l,t), (x,t)∈×(0,T],

u(x,0)=φ(x),v(x,0)=φ(x),x∈.

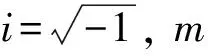
在此物理模型中通常有以下几类守恒量.

这几类守恒量很可能与时间方向上的精度密切相关.近十年来，人们提出了大量的数值方法来解决CSK方程，如有限元方法(finite element method,FEM)[5]、径向基函数配点法[6]、分解法[7]、变分迭代[8]、Padé有理逼近的指数时间差分三层隐式格式(exponential time differencing three-layer implicit scheme,ETDT-P)[9]、同伦摄动[10]及四阶紧致差分格式(fourth-order conservative compact finite difference scheme,FCS)[4]等.

本文首先介绍六阶紧致差分格式并将其用于CSK方程的数值求解，随后提出一种六阶紧致差分格式的通用矩阵形式并分析该格式的离散守恒性，最后给出数值实验的结果.

1 六阶紧致差分格式

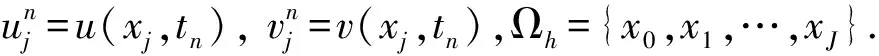
注意到空间一阶导数在每点上的六阶紧致差分[11]近似

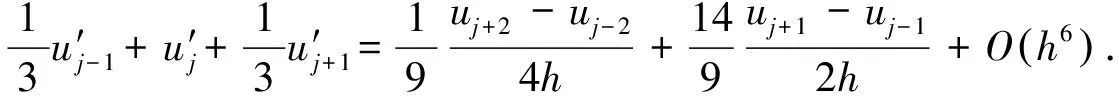
(1)

通过计算及以上算子的定义，式(1)可以写成如下算子形式:

(2)

类似地，空间二阶导数的六阶紧致差分[11]近似为

等价于

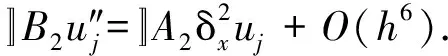
(3)

结合式(2)和(3)，可得空间三阶导数的六阶差分近似为

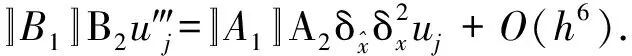
(4)

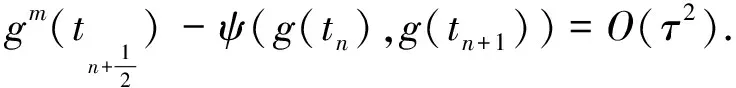
(5)

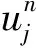
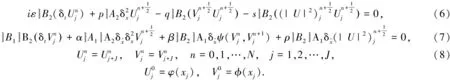
(9)

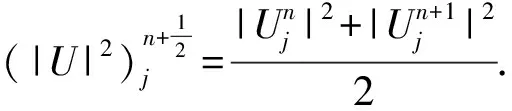
2 守恒性分析

2.1 记号与引理

记Hp(Ωh)={u|u={uj},j=0,1,…,J,uj=uj+J}为定义在Ωh上以J为周期的实值或复值网格函数所组成的空间.网格函数空间Hp(Ωh)上的离散内积及其相应离散L2-范数和L∞-范数定义如下：

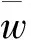
引理1对于任意网格函数u,w∈Hp(Ωh)，以下等式成立：

引理2对于任意网格函数u,w∈Hp(Ωh)，以下等式成立：

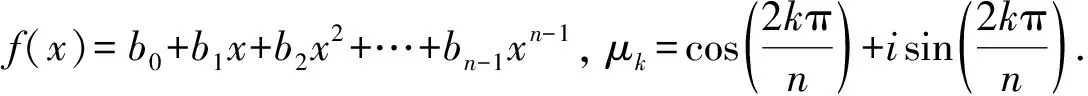
由引理3，易得如下结果：

引理4[13]对于任意网格函数u,w∈Hp(Ωh)，以下不等式成立：

2.2 守恒性

关于CSK方程, Xie等[4]给出了一个四阶紧致格式的守恒性，本文构造的格式(6)、(7)是一个六阶紧致格式，其守恒性定理有：

定理1格式(6)、(7)保持如下离散守恒性：

‖Un‖2=‖U0‖2,

(10)

(11)

证明令

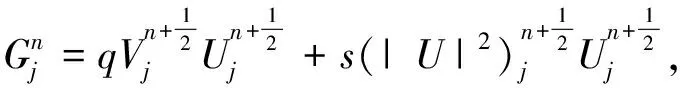
(12)

结合式(6)和(12)得

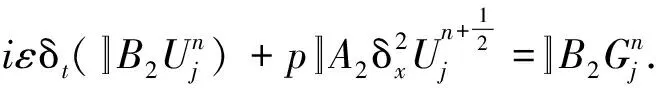
(13)

(16)

将式(16)两边同时乘以iε并利用内积的共轭对称性可得

(17)

由引理1、式(15)和(17)得

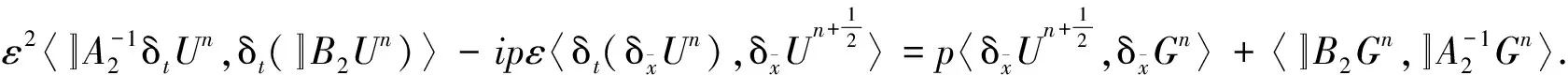
(18)

(19)

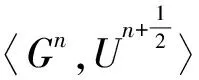
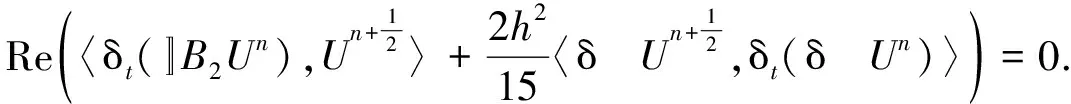
(20)

将引理1用于式(20)，即得‖Un+1‖2=‖Un‖2.将式(7)与向量1∶=(1,1,…,1)T∈Hp(Ωh)进行内积运算，可得

〈B1B2Vn+1,1〉=〈B1B2Vn,1〉.

再利用周期性边界条件，即得式(11)成立.

以下定义

易知格式(6)、(7)等价于以下矩阵形式：

其中循环对称矩阵A1,A2,B1,B2是分别对应于算子A1,A2,B1,B2的J阶方阵，记为

方程(6)和(7)可写成如下等价形式：

(22)

定理2格式(6)、(7)保持如下离散守恒性：

n=0,1,…,N.

(23)

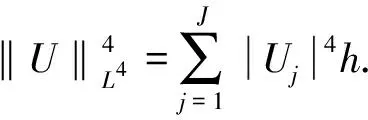
证明将式(21)与δtUn进行内积运算并利用循环矩阵的可交换性，可得

(24)

取式(24)的实部得

(25)

将式(25)两边同时乘以2τ并将上标从0至n求和，可得

(26)

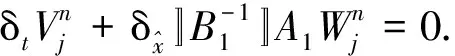
(27)

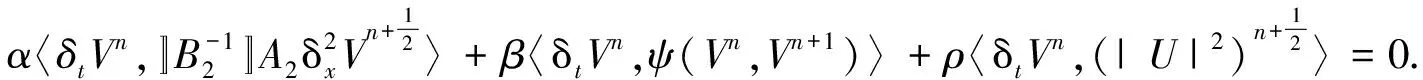
(28)

由ψ(Vn,Vn+1)的定义，易得

以及

将式(28)两边同时乘以2τ并将上标从0至n求和，可得

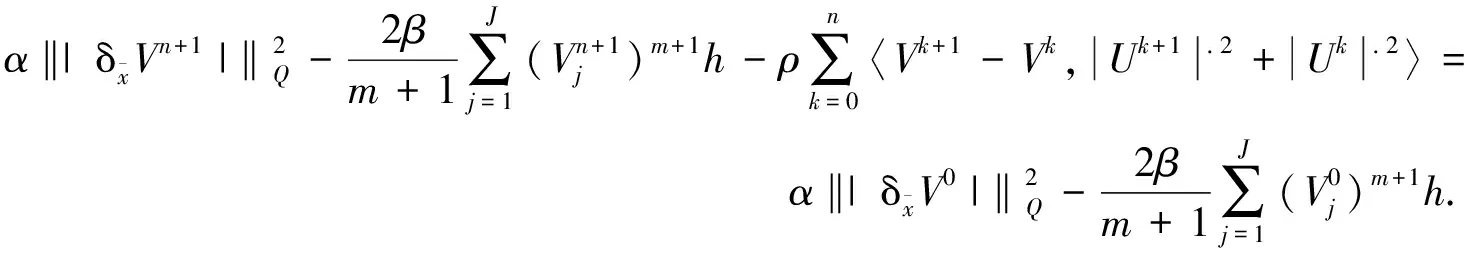
(29)

又因为

方程(29)等价于

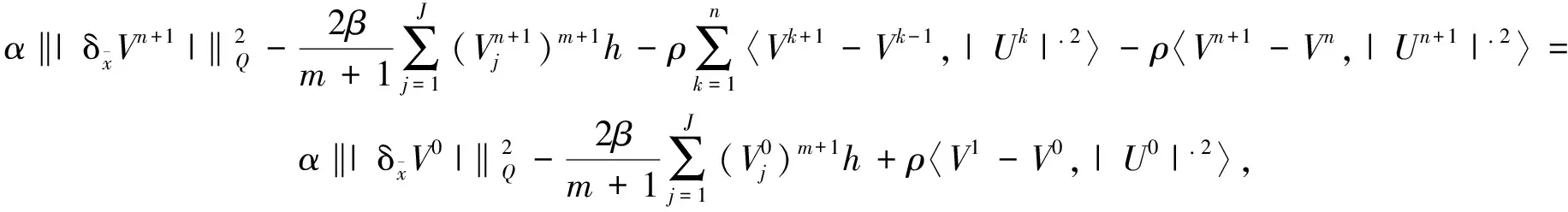
(30)

将式(26)和(30)分别乘以ρ和q/2并相减,即得式(23)成立.

因格式(6)和(7)是非线性的，计算较为复杂，为了保持格式原有的计算精度，本文将其转化为如下线性迭代格式：

(34)

其中U*0=(U0*+U0)/2,U*n=(3Un-Un-1)/2,Un*=2Un-Un-1,n≥1.

可以证明线性格式(33)、(34)在时间和空间上分别是二阶和六阶收敛的.

3 数值实验

本节给出一些例子来说明所提出格式的守恒性和六阶精度.记守恒量I1,I2,I3和I4的离散形式为

守恒量的误差定义为

此外,本文用L2-范数(‖u-U‖+‖v-V‖)及L∞-范数(‖u-U‖L∞+‖v-V‖L∞)来检验所提出格式的精度.

例1[10]考虑如下柯西问题：

iut+uxx-vu=0, (x,t)∈×(0,T],

vt+vxxx+(3v2+|u|2)x=0, (x,t)∈×(0,T],

u(x,0)=φ(x),v(x,0)=φ(x),x∈.

其解析解为u(x,t)=exp(i(x+t/4)),v(x,t)=3/4,在h=π/20、τ=0.001、空间域取[0,2π]的情况下数值求解CSK方程，表1列出了不同时刻的各个守恒量误差，佐证了所提出格式的守恒性.

表1 不同时刻的各个守恒量误差Tab.1 Errors of invariants at different time

取h=π/10,τ=0.1,表2列出了不同时刻不同步长下的两种范数误差，验证了所提出格式在空间上六阶收敛.

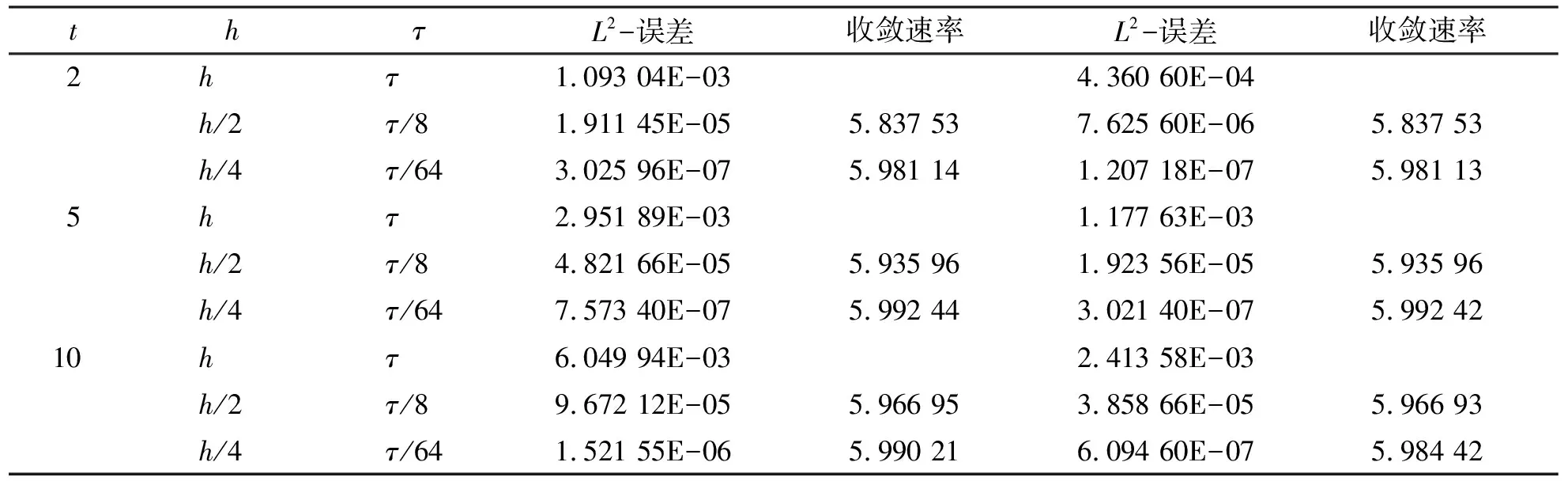
表2 不同时刻的收敛速率Tab.2 Convergence rates at different time

例2[5]考虑如下耦合问题：

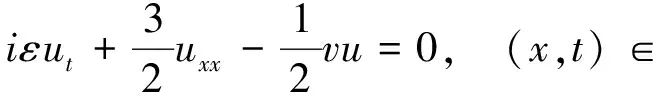
其解析解为

其中c是任意正常数，初始条件为

此外，为满足CSK方程的物理意义即当|x|趋于无穷时|u|和v趋于0，设置边界条件为u(a,t)=u(b,t)=0,v(a,t)=v(b,t)=0.取参数ε=1,c=0.45，在h=0.25、τ=0.000 01、空间域取[-30,30]的情况下数值求解CSK方程.表3列出了t=0.001时，U(x,t)虚部数值解(ImU)、实部数值解(ReU)、V(x,t)的数值解及其误差范数(‖ImEu‖, ‖ReEu‖, ‖Ev‖)，以及与其他方法和精确解的比较.由表3可见，本文方法与其他方法具有相近的误差范数(实际上这是边界误差造成的，因为此时空间和时间上的内部误差都远小于边界误差)，而在离边界较远的内点(如0)上，本文方法的精度远远大于其他方法.图1模拟了|U|、V的数值解和解析解从t=0到t=30的演变过程，可以发现数值解与精确解高度一致.

表3 本文方法数值解与其他方法及精确解的比较 Tab.3 Comparison of numerical solutions with exact solutions and other methods

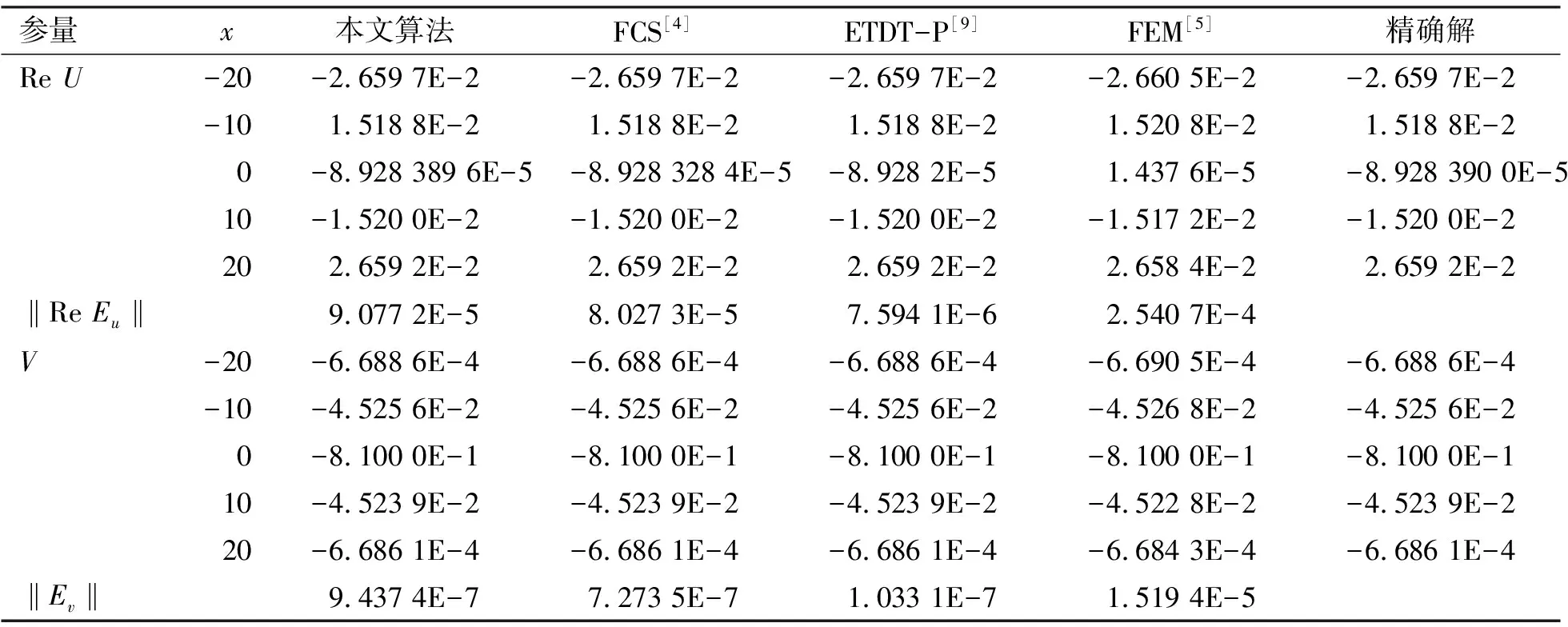
续表3

注：t∈[0,30],[a,b]=[-70,30],h=0.5,τ=0.001.

4 结束语

通过构造数个循环对称阵得到一种通用的六阶紧致差分格式并将其用于数值求解耦合Schrödinger-KdV(CSK)方程.利用CSK方程的几类守恒量对该数值方法的性能进行了衡量.数值实验说明了该方法的精度和稳定性，特别是在内点取得了较其他方法更高的精度.因为六阶紧致差分格式中构造的数个矩阵具有与四阶紧致差分格式中矩阵类似的性质，该格式还可推广到其他用四阶紧致差分格式求解的方程如Klein-Gordon-Schrödinger方程[15]、耦合Gross-Pitaevskii方程[16]等.