Banach代数中Zhou逆加法性质及其应用

杨 杰，刘大勇，陈焕艮

(1. 杭州师范大学数学学院，浙江 杭州 311121； 2. 中南林业科技大学理学院，湖南 长沙 410004)

设A表示具有单位元1的Banach代数.称a是Drazin可逆，如果存在x∈A，满足

ax=xa,xax=x,a-a2x∈N(A>),

x称为a的Drazin逆.如果它存在，则是唯一的，x写作aD.这里N(A>)是A中所有幂零元构成的集合.Drazin逆在微分和差分方程、Markov链、控制理论等许多领域都有广泛的运用[1-2].

Koliha[3]引进了广义Drazin逆，如果存在a∈A,ad∈A满足以下条件：

adaad=ad,aad=ada,a-a2ad∈Aqnil.

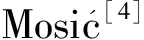
可以证明a∈A是交换的幂等元与幂零元的和当且仅当a-a2∈N(A>)，a∈A是交换的tripotent元与幂零元的和当且仅当a-a3∈N(A>)[6].为了用广义逆方法刻画Banach代数中元素的周期和幂零分解，文[6]引进了一类新型广义逆——Zhou逆.假定a∈A，称a具有Zhou可逆，如果存在x∈A,n∈满足以下条件：

x=xax,ax=xa,an-ax∈N(A>).

如果x存在，那么它是唯一的，且记作aZ，并称为a的Zhou逆.Zhou逆是Drazin逆， 但反之不然.Zhou逆的基本性质参见文[6].

本文给出了Banach代数中Zhou逆的一个新的加法性质.设a,b∈AZ.如果a2ba=0,ab2=0，证明了a+b∈AZ.然后将这些结果应用到算子矩阵上，研究了Banach代数上分块算子矩阵的Zhou可逆性，获得了新的Zhou可逆算子矩阵，由此刻画了分块算子矩阵的一类分解性质.

本文中，所有的Banach代数都是带有单位元的复Banach代数，AZ表示所有A中的Zhou可逆元集合，N(A>)表示A中所有幂零元素的集合，aπ表示元素a∈AZ的谱幂等元1-aaZ.

1 Zhou逆的性质

引理1设A是Banach代数.如果a∈A，那么以下条件等价：

1)a∈AZ.

2)存在n∈，使得a-an+1∈N(A>).

证明由[6，定理4.1]即得.

引理2如果a,b∈AZ，ab=ba，那么ab∈AZ.

证明因为a,b∈AZ，有m,n∈使得a-an+1,b-bm+1∈N(A>)，从而

ab-(ab)mn+1=ab-amn+1bmn+1=(a-amn+1)b+amn+1(b-bmn+1)∈N(A>).

根据引理1，得ab∈AZ.

引理3设a∈A,n∈，则a∈AZ当且仅当an∈AZ.

证明⟹.根据a∈AZ，有m∈使得a-am+1∈N(A>).从而有

an-(an)m+1=an(1-amn)=an(1-am)[(am)n-1+(am)n-2+…+(am)2+am+1]=

an-1(a-am+1)[(am)n-1+(am)n-2+…+(am)2+am+1]∈N(A>).

根据引理1，可知an∈AZ.

⟸.由于an∈AZ，那么an-(an)m+1∈N(A>)，即an-an+mn∈N(A>)，从而an-1[a-amn+1]∈N(A>),故

[1-amn]n-1an-1[a-amn+1]∈N(A>).

所以[a-amn+1]n∈N(A>)，则存在k∈，有(a-amn+1)nk=0，由引理1即得a∈AZ.

下面把Drazin逆的Cline公式推广到Zhou逆.

定理1设a,b∈A.如果ab∈AZ，则ba∈AZ.

证明因为ab∈AZ,存在m∈使得ab-(ab)m+1∈N(A>).因此存在k∈使得[ab-(ab)m+1]k=0.从而

[ba-(ba)m+1]k+1=ba(1-(ba)m)ba(1-(ba)m)…ba(1-(ba)m)ba(1-(ba)m)=

b[ab-(ab)m+1]ka[1-(ba)m]=0，

即ba-(ba)m+1∈N(A>).根据引理1可知ba∈AZ.

推论1设A∈Mm×n(A>),B∈Mn×m(A>).如果AB∈Mm×m(A>)Z，那么BA∈Mn×n(A>)Z.

证明假设m≥n，则有

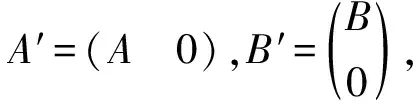
再利用引理1即得BA∈Mn×n(A>)Z.

2 加法性质

本节研究Banach代数中两个元素和的Zhou可逆性.我们有

证明因为a,b∈AZ，从而存在m,n∈使得a-am+1,b-bn+1∈N(A>).因此，

a-amn+1=a[1-(am)n]=a(1-am)[1+am+(am)2+…+(am)n-1]=

(a-am+1)[1+am+(am)2+…+(am)n-1]，

所以a-amn+1∈N(A>).类似地，有b-bmn+1∈N(A>).因此，

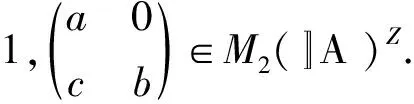
引理5设A是Banach代数且a,b∈AZ.如果ab=0，则a+b∈AZ.

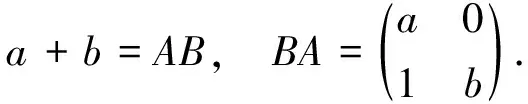
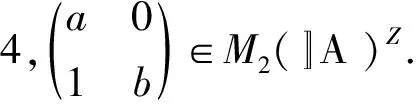
定理2设A是一个Banach代数且a,b,ab∈AZ.如果a2ba=0,ab2=0，则a+b∈AZ.

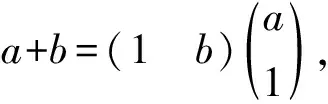
进一步，由a2ba=0,ab2=0可得

因此根据引理5，P+Q有Zhou逆，从而M2有Zhou逆.故M有Zhou逆，再利用推论1即得a+b∈AZ.

推论2设A是Banach代数，a,b∈AZ.如果ab2=0,aba=0，则a+b∈AZ.

证明根据条件可知a,b,ab∈AZ和a2ba=0,ab2=0.由定理2即可得.

定理3设A是一个Banach代数，且a,b,ab∈AZ.如果bab2=0,a2b=0，则a+b∈AZ.

由bab2=0,a2b=0，所以

因此根据引理5，P+Q有Zhou逆，从而M2有Zhou逆.故M有Zhou逆.利用推论1，可得a+b∈AZ.

推论3设A是Banach代数，a,b∈AZ.如果a2b=0,bab=0，则a+b∈AZ.

证明根据定理3可得.

如例1所示，定理2中条件比一般正交性条件更广泛.

例1设A=2×2.取则a,b,ab∈AZ且有a2ba=0,ab2=0,但是a2b≠0.

证明因为

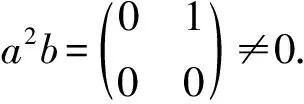
由于a-aaD=0,(b-bbD)2=0，因此有a,ab=b∈AZ.

3 算子矩阵Zhou逆

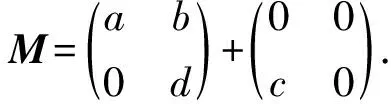
因此根据推论2可得M∈M2(A>)Z.

证明由定理4易得.

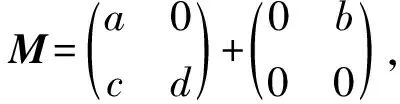
由推论2，可得M∈M2(A>)Z.

证明由定理5即得.

进一步有：

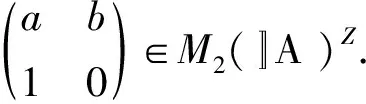
证明显然，我们有

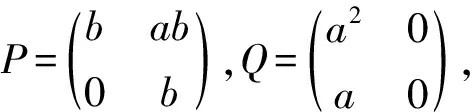
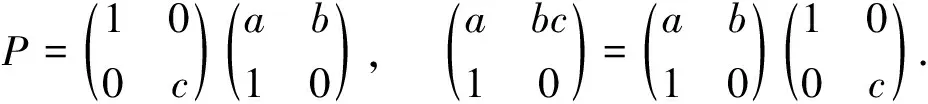
由定理1，P有Zhou逆.因为bdc=0,bd2=0，有

根据推论2，M=P+Q∈M2(A>)Z.

证明由bcb=0得(bc)2=0，所以bc∈AZ.因为bd=0，所以bdc=0,bd2=0.根据定理6即得.

证明因为a(bc)=(bc)a，所以aD(bc)=(bc)aD，故aZ(bc)=(bc)aZ.从而由引理2得bcaZ∈AZ.利用定理1可知，caZb∈AZ.设

显然Q有Zhou逆.由caZb∈AZ,a(aZ)2=aZ和定理1，aaZbcaZ∈AZ.根据引理2，a2aZ∈AZ.注意到(a2aZ)(1+aaZbcaZ)=(1+aaZbcaZ)(a2aZ)，根据引理2，

a2aZ+aaZbcaZ=a2aZ(1+aZbcaZ)∈AZ，

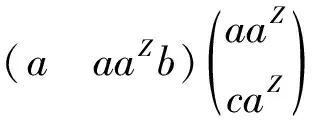
a(bc)=(bc)a，所以aD(bc)=(bc)aD，故aaD(bc)=(bc)aaD.因此，

aπ(bc)=bc-aaD(bc)=bc-(bc)aaD=(bc)aπ.

由bc∈AZ,aπ∈AZ,知aπ(bc)∈AZ,从而caπb∈AZ.由定理4得PQ有Zhou逆.

已知aaπbc=0,abc=bca，可以验证PQ2=0,

根据定理2推出

证明因为abc=0,bca=0，所以aaπbc=0,abc=bca.进一步有1+aZbcaZ=1+(aZ)2(abc)aZ=1∈AZ，由定理7即得.