基于矩阵半张量积解特殊结构的四元数线性系统
王 涛,李 莹,丁文旭,韦安丽
(聊城大学数学科学学院,山东 聊城 252000)
0 引言
对于矩阵方法在多线性乃至非线性问题计算上的运用,其矩阵表示是一个不可避开的关键问题.对此,程代展等给出了一个便捷的新工具——矩阵半张量积[1].矩阵半张量积是普通矩阵乘法的推广,不仅消除了普通矩阵乘法在维数上的限制,并且具有比推广前更好的性质——伪交换性[1],因此在有限博弈[2]、布尔网络的分析与控制[3]、模糊系统分析与设计[4]、混合值逻辑网络的控制与应用[5]等许多问题的研究中起着重要的作用.本文将矩阵半张量积的应用进一步拓展到了求解具有特殊结构的四元数Toeplitz线性系统
Ax=b
(1)
的计算问题中.


近年来,四元数矩阵在数学[6]、计算机软件及计算机应用[7]、航空航天科学与工程[8]、电信技术[9]等领域有着广泛的应用,因此四元数和四元数矩阵的研究显得愈发重要.本文将研究四元数体中的Toeplitz线性系统.工程计算中的诸多问题最后都能归结为线性系统的求解,Toeplitz线性系统的求解是其中非常重要的一类.例如,在图像复原领域中,可以通过构造特定结构的循环矩阵,将退化模型逆求解转化成Toeplitz线性系统的求解,然后基于Toeplitz线性系统的相关理论,给出模型逆求解的快速求解方法,使复原算法具有较高的运算效率[10].Toeplitz线性系统的求解可采用直接法与迭代法进行.直接法包括Zohar算法、Bareiss变换法、Akaike算法等[11].迭代法包括Michael针对Toeplitz矩阵的特殊结构提出的循环与反循环分裂迭代法CSCS(将Toeplitz矩阵分裂为一个循环矩阵与一个反循环矩阵再进行双步迭代求解)[12]、基于CSCS的快速CSCS分裂迭代法(该方法能够在一定条件下收敛于Toeplitz线性系统的唯一解)[13],以及求解复线性系统的特殊Toeplitz解的矩阵半张量积方法[14].本文采用直接法,利用四元数的实向量表示与矩阵半张量积直接求解特殊结构下的四元数Toeplitz线性系统,并用数值例子验证了该方法的有效性.
1 预备知识
定义1[15]设x=x1+x2i+x3j+x4k∈Q,其中,xi∈(i=1,2,3,4),且i,j,k满足如下运算法则:
i2=j2=k2=-1,ij=-ji=k,jk=-kj=i,ki=-ik=j.
定义2[16]设A∈Rm×n,B∈Rp×q,n与p的最小公倍数为t=lcm(n,p),则A与B的半张量积定义为
当n=p时,矩阵半张量积转化为普通矩阵乘法,因此矩阵半张量积是普通矩阵乘法的一个推广,它保持了普通矩阵乘法的所有性质,在矩阵相关的理论研究中是极其方便的.
引理1[16]设x∈Rm,y∈Rn,则x*y=x⊗y.
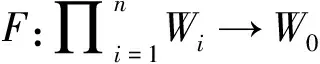
MF称为F的结构矩阵.
普通矩阵乘法有维数限制与不可交换性两大弱点,由定义2可以看到,矩阵半张量积彻底克服了第一个弱点.以下说明矩阵半张量积在一定程度上也可以克服第二个弱点,即具有一定程度的交换性.
定义4[16]定义换位矩阵W[m,n]∈Rmn×mn,
引理2[16]设x∈Rm,y∈Rn,则W[m,n]*x*y=y*x.
引理3[16]设x∈Rm,A∈Rm×n,则x*A=(Im⊗A)*x.
引理4[17]设A∈Rm×n,b∈Rm,当且仅当AA†b=b时,线性方程Ax=b有解,且通解表示形式为x=A†b+(In-A†A)y,∀y∈Rn.
2 四元数矩阵的实向量表示
定义5设x=x1+x2i+x3j+x4k∈Q,其中xi∈,称v(x)=(x1,x2,x3,x4)T为四元数x的实向量表示.
借助定义的四元数的实向量表示,可以将两个四元数乘积的实向量表示转化为两个四元数实向量表示的矩阵半张量积运算.
引理5[6]设x,y∈Q,则
v(xy)=MQ*v(x)*v(y),

通过定义5,给出四元数行、列向量的实向量表示的定义.
定义6设x=(x1,x2,…,xn)∈Qn,y=(y1,y2,…,yn)T∈Qn,称
v(x)=(v(x1),…,v(xn))T,v(y)=(v(y1),…,v(yn))T
为四元数向量x,y的实向量表示.
利用四元数向量的实向量表示,可以得到以下性质.

2)‖b‖=‖v(b)‖;
证明1)和2)简单计算可得到,下面给出3)的证明.
v(ab)=v(a1b1+…+anbn)=v(a1b1)+…+v(anbn)=
MQ*v(a1)*v(b1)+…+MQ*v(an)*v(bn)=
类似地,定义出四元数矩阵的实向量表示.
定义7设A=(aij)∈Qm×n,定义Colj(A),Rowi(A)(j=1,…,n,i=1,…,m)为四元数矩阵A的第j列和第i行,则
称为四元数矩阵A的实列排与实行排.
下面研究四元数矩阵的实向量表示的性质.

证明1)和2)容易验证,仅对3)进行证明.首先将矩阵A按行进行分块,即
3 问题1和2的代数解
本节将研究问题1和问题2的代数解.首先,根据四元数三对角Hermitian矩阵与三对角反Hermitian矩阵的特点,提取矩阵中的有效元素,记为独立元素.通过矩阵的独立元素的实向量表示给出矩阵的实向量表示,减小问题的计算规模.


(2)


(HH†-I4n)v(b)=0,
(3)
此时,通解x满足表达式
TH={v(x)=H†v(b)+(I4n-H†H)y,∀y∈R4n},
(4)
其极小范数解xH满足
v(xH)=H†v(b).
(5)
证明由定理1中性质3),可得
‖HH†Hv(x)-v(b)‖=‖HH†v(b)-v(b)‖=‖(HH†-I4n)v(b)‖,
即
‖Ax-b‖=0⟺‖(HH†-I4n)v(b)‖=0⟺(HH†-I4n)v(b)=0,
所以式(3)成立.对于实矩阵方程Hv(x)=v(b),根据引理4,可以给出四元数矩阵方程(1)的通解表达式及极小范数解.从而,式(4)、(5)成立.
根据定理3与4,相似地,可以得到四元数三对角反Hermitian矩阵的性质及问题2的答案.



TAH={x∈Qn|v(x)=W†v(b)+(I4n-W†W)y,∀y∈R4n},
(6)
其极小范数解xAH满足
v(xAH)=W†v(b).
(7)
4 数值算法与算例


算例1在Matlab中,首先利用“rand”与“Toeplitz”函数随机生成Toeplitz矩阵Ai、实向量xi(i=1,2,3,4),再利用函数“Tril”与“Triu”生成三对角Toeplitz矩阵,最后利用“quaternion”工具包生成四元数向量x=x1+x2i+x3j+x4k和四元数三对角Hermitian(反Hermitian)矩阵:


从图1可得,真实解与计算得到的解之间的误差很小,说明此计算方法有效.
5 结论
基于矩阵半张量积,利用四元数矩阵的实向量表示方法将四元数上具有特殊结构的Toeplitz线性系统Ax=b的问题转化为实数域上的相应问题,给出了四元数Toeplitz线性系统相容时的充要条件及通解表达式,并通过给出的数值例子的误差实验来说明算法的有效性.

