四种半张量积及其代数关系

冯俊娥 李怡靓 赵建立

(1.山东大学 数学学院，山东 济南 250100； 2.聊城大学 数学科学学院，山东 聊城 252059)

0 引言

矩阵半张量积最早是由程代展研究员提出的一种新的矩阵乘积[1]，我们称之为1-型矩阵半张量积.1-型矩阵半张量积克服了传统矩阵乘积对维数的限制，因此，1-型矩阵半张量积在许多领域都有着重要的应用，例如：逻辑网络[2-4]，博弈论[5-7]，模糊系统[8-10]等，并且矩阵半张量积在工程中亦有重要的应用[11].

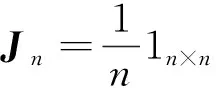
本文我们将给出这四种矩阵乘积的定义，研究这四种矩阵乘积之间的代数关系，并将两种矩阵与向量的半张量积形式上推广到矩阵与矩阵的半张量积，这里我们称之为3-型矩阵半张量积与4-型矩阵半张量积.容易验证3-型矩阵半张量积与4-型矩阵半张量积不满足矩阵乘法的结合律，但可以把它们看做是矩阵与一些列向量集合的乘积，并且3-型矩阵半张量积以及4-型矩阵半张量积与1-型矩阵半张量积和2-型矩阵半张量积也有一定代数关系，因此通过研究它们之间的关系，可以更深入地掌握几种矩阵半张量积的代数性质.

本文将用到的一些记号：

(1)In：n维单位矩阵；

(2) 1m×n：元素全为1的m×n维列矩阵；

(3) 1n：元素全为1的n维列向量；

(4)Rowi(A)(Coli(A))：矩阵A的第i行(列)；

(5) 矩阵Am×n,Bp×q的Kronecker积定义为

1 矩阵半张量积及其推广

首先引入1-型矩阵半张量积与2-型矩阵半张量积[12].

定义1给定矩阵Am×n,Bp×q,定义两个矩阵的1-型矩阵半张量积与2-型矩阵半张量积分别为

其中l=[n,p]表示两个正整数n与p的最小公倍数，而⊗表示两个矩阵的张量积(也称Kronecker积)，Iw表示w维单位矩阵.

当两个矩阵Am×n,Bp×q的维数相容时，即n=p时，1-型矩阵半张量积与2-型矩阵半张量积皆为传统的矩阵乘积，并且它们都满足矩阵的结合律等性质，具体可以参见文献[12].

下面我们给出1-型MV半张量积与2-型MV半张量积[12].

定义2给定矩阵Am×n与向量xp，定义1-型MV半张量积与2-型MV半张量积分别为

其中1w表示w维各元素全为1的列向量.显然，当n=p时，1-型MV半张量积与2-型MV半张量积皆为传统的矩阵与向量的乘积.

受定义2启发，我们将1-型MV半张量积与2-型MV半张量积推广到矩阵与矩阵相乘的情形，我们称之为3-型矩阵半张量积与4-型矩阵半张量积.

定义3给定矩阵Am×n,Bp×q,定义两个矩阵的3-型矩阵半张量积与4-型矩阵半张量积分别为

显然当矩阵B为列向量时，3-型矩阵半张量积与4-型矩阵半张量积即为1-型MV半张量积与2-型MV半张量积.上面的3-型矩阵半张量积与4-型矩阵半张量积是良定的，但它们并不满足矩阵的结合律等性质.我们可以把3-型矩阵半张量积与4-型矩阵半张量积定义中的矩阵B看成是一些列向量的集合，此时定义3自然是定义2的一个推广.不仅如此，定义3与定义1也有一定的代数关系，因此它的定义也有助于我们进一步地研究1-型矩阵半张量积与2-型矩阵半张量积的代数性质.

2 几种矩阵半张量积的代数性质

本节讨论几种矩阵半张量积的代数性质，这里本文主要考虑三种情形：(1) 矩阵与向量的半张量积；(2) 矩阵与矩阵的半张量积；(3) 向量与向量的半张量积.

2.1 矩阵与向量的半张量积

首先讨论矩阵与列向量的1-型MV半张量积与2-型MV半张量积和1-型矩阵半张量积之间的关系，我们有下面的定理.

定理1给定矩阵Am×n与列向量xp，且l=[n,p]，则有下面的结论成立

(1)

(2)

证明首先证明结论(1)，利用1-型MV矩阵半张量积的定义，直接计算可得

经过简单计算可得

由1-型矩阵半张量积的定义即得(1)式右边.

下面证明结论(2)，利用2-型MV矩阵半张量积的定义得

上式经过简单计算可得

由1-型矩阵半张量积的定义即得(2)式的右边.定理得证.

由定理1的结论直接可得1-型MV半张量积与2-型MV半张量积之间的代数关系.

推论1给定矩阵Am×n与向量xp，且l=[n,p]，则有

下面讨论1-型矩阵半张量积与2-型矩阵半张量积作用于矩阵与列向量时的代数关系.

定理2给定矩阵Am×n与向量xp，且l=[n,p]，则有

证明利用2-型矩阵半张量积的定义，计算可得

经过简单计算，可由上式得

进一步，上式可化简为

由1-型矩阵半张量积的定义即得定理2.定理证毕.

2.2 矩阵与矩阵的半张量积

本小节讨论两个矩阵的3-型矩阵半张量积与4-型矩阵半张量积和1-型矩阵半张量积与2-型矩阵半张量积之间的关系.

由3-型矩阵半张量积与4-型矩阵半张量积的定义以及定理1，直接有下面的结论.

定理3给定矩阵Am×n与Bp×q，且l=[n,p]，则有

(3)

(4)

由2-型矩阵半张量积的定义与定理3的结果可得1-型矩阵半张量积与2-型矩阵半张量积之间的代数关系.

定理4给定矩阵Am×n与Bp×q，且l=[n,p]，则有

(5)

证明由2-型矩阵半张量积的定义得

由定理3的(3)即得定理4结论.定理证毕.

2.3 向量与向量的半张量积

本小节讨论两个向量的1-型MV矩阵半张量积与2-型MV矩阵半张量积和1-型矩阵半张量积与2-型矩阵半张量积之间的关系.

首先讨论两个列向量的几种矩阵半张量积之间的关系.

定理5给定列向量xn与yp，则有

(6)

(7)

证明(6)式由1-型MV矩阵半张量积，1-型矩阵半张量积以及张量积的定义直接可得.这里只证明(7)式，

定理证毕.

当两个向量为行向量时，我们有下面的结论.

定理6给定行向量xn与yp，则有

x×1y=y⊗x.

(8)

(9)

(10)

证明(8)式由1-型矩阵半张量积以及张量积的定义直接可得.这里只给出(9)式(10)式的证明.

(10) 由2-型矩阵半张量积定义，计算可得

定理证毕.

本文所讨论的几种矩阵半张量积都是左半张量积[1,12],相应地，我们也可以定义几种矩阵半张量积的右半张量积形式[12].对于矩阵的右半张量积也有类似的性质，这里不再赘述.

3 结束语

本文分矩阵与矩阵，矩阵与向量，向量与向量三种情形，研究了几种矩阵半张量积的代数关系.同时将1-型MV半张量积与2-型MV半张量积推广到矩阵与矩阵的乘积情形，即3-型矩阵半张量积与4-型矩阵半张量积，本文得到的所有结论都可以推广到矩阵的右半张量积的情形.