利用“筝形”公式求外接球半径
2022-11-28 08:09:34陈淑红
高中数学教与学 2022年19期
陈淑红
(河北省定州中学,073000)
有关外接球的问题综合性强,思维难度大,学生常常为此望而生畏.本文从不规则的空间结构中提炼出筝形公式,代入求解外接球半径,形成有法可依、有规可循的解题方法体系.
首先从外接圆到外接球,确定外接球球心的位置.如图1,由于球心O在过截面圆心且与截面垂直的直线上,则过两截面圆心O1与O2且与两截面垂直的直线O1O与O2O之交点O即为多面体外接球球心.

其次,取两截面圆公共弦AB的中点M,则∠O1MO2为两截面二面角的平面角.易知O,O1,M,O2四点共圆,则OM为此圆的半径.

OB2=OM2+BM2

因四边形OO1MO2形状为筝形,所以我们不妨称上述半径公式为“筝形”公式.

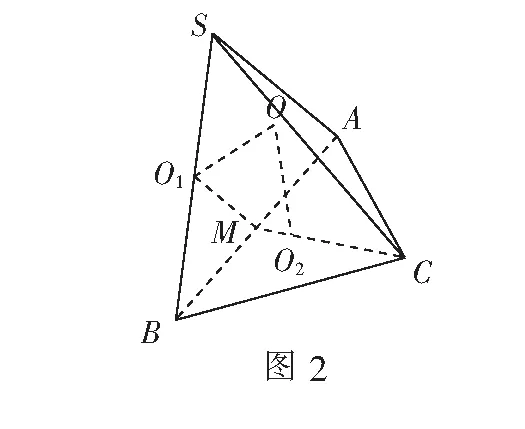
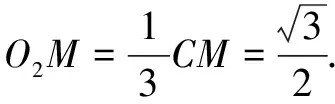
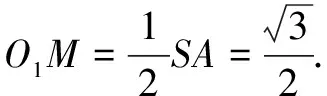
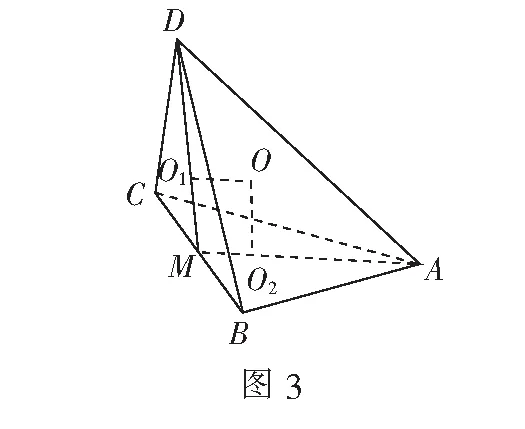
例2如图3,在四面体ABCD中,有一条棱长为3,其余5条棱长皆为2,则该四面体外接球的半径为______.
解不妨设BC=3,取BC的中点M,则∆ABC的外心O2在AM上.根据勾股定理,有
O2B2=MB2+(AM-AO2)2
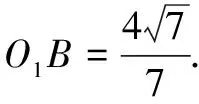
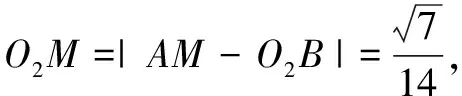
因为∠AMD为二面角A-BC-D的平面角,故可在∆AMD中用余弦定理的逆定理,得
由上可见,利用筝形公式求外接球半径,关键是选择表面多边形,注意选择特殊性状的多边形(如正三角形、直角三角形、等腰三角形等),比较容易确定多边形外心位置,求出外接圆半径的大小.
猜你喜欢
中学生数理化(高中版.高考数学)(2022年2期)2022-04-26 14:05:04
中学数学教学(2019年3期)2019-06-21 08:10:52
中等数学(2018年8期)2018-11-10 05:07:22
中学生数理化(高中版.高二数学)(2018年1期)2018-02-26 07:40:29
中学数学杂志(高中版)(2018年1期)2018-01-27 18:49:49
教学考试(高考数学)(2017年2期)2017-08-11 12:10:19
福建中学数学(2016年4期)2016-10-19 05:09:02
综合智慧能源(2016年1期)2016-02-03 10:04:44
中学教学参考·理科版(2014年3期)2014-04-10 09:12:52
新课程·中旬(2014年12期)2014-03-27 13:32:11

