还是坐标平移好
2022-11-28 08:37单墫
高中数学教与学 2022年19期
单 墫
(南京师范大学数学科学学院,210023)
解析几何中的坐标平移,简明清晰,解题时常可以用来化繁为简,而且体现了运动与变换,应当引入教材.
以2022年新高考为例,一个例子是今年新高考全国I卷第21题,原题如下.

(1)求l的斜率;

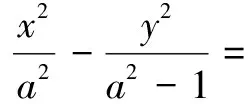
x2-2y2=2.
①
更一般地,考虑点A(x0,y0),曲线C:px2+qy2=t.作坐标平移
则在uv平面中,A为原点,而C的方程变为
p(u+x0)2+q(v+y0)2=t,
展开为
pu2+qv2+ru+sv=0,
②
因为曲线C过原点A,所以② 式中的常数项为0,不必计算,而r=2px0,s=2qy0.
设直线l的方程为mu+nv=1,则有齐次方程
pu2+qv2+(ru+sv)(mu+nv)=0,
③
它表示过原点A的直线AP,AQ.

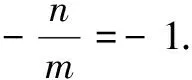
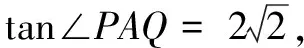



另一个例子是今年新高考全国乙卷第20题,很多人反映计算量大,其实作一个平移即可化繁为简.

(1)求椭圆E的方程;
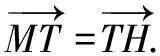

(2)令v=y+2,平移x轴以A(0,-2)为新的原点.则在xv坐标系中,E的方程为4x2+3(v-2)2=12,即
4x2+3v2-12v=0.
④

3v=2x,
⑤
设过点P(新坐标为P(1,0))的直线方程为
x=hv+1.
⑥
M,N两点的坐标(x1,v1),(x2,v2)满足④ 和⑥ 式,所以也满足4(hv+1)2+3v2-12v=0,即
(4h2+3)v2+(8h-12)v+4=0.
⑦
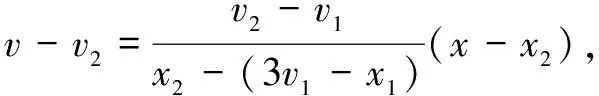
而v2(3v1-x1)-x2v1
=3v1v2-x1v2-x2v1
=(3-2h)v1v2-(v1+v2)
=0,
所以直线HN过点A(定点).
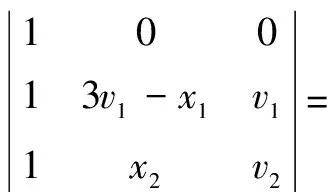
真不明白编课程标准的人为什么不将坐标平移列入课程.
猜你喜欢
声屏世界(2022年17期)2022-12-18
数理化解题研究·高中版(2022年4期)2022-04-28
物理之友(2022年1期)2022-04-19
教学考试(高考生物)(2021年5期)2021-12-24
江苏教育(2021年54期)2021-08-31
中小学校长(2021年7期)2021-08-21
疯狂英语·爱英语(2021年4期)2021-08-16
语数外学习·初中版(2020年2期)2020-09-10
中学生数理化·高一版(2020年2期)2020-04-21
校园英语·上旬(2019年8期)2019-09-16

