再探抛物线中的“蝴蝶之谜”
2022-11-28 08:09万建光李佳一
高中数学教与学 2022年19期
万建光 李佳一
(湖北省武汉市吴家山第三中学,430040) (湖北省襄阳市第一中学,441099)
袁晶老师在文[1]中给出的抛物线中的“蝴蝶之谜”是由圆中的蝴蝶定理类比而来,并给出了两种方法解开了其中的奥秘.抛物线也是一种轴对称图形,能否有更一般性的结论?有没有其他更加简捷易懂的解法?图形中还有哪些结论?笔者为此深入探究,发现原文中的焦点F的位置可以更一般化,只需满足在抛物线的对称轴上即可.现将相应的结论及其推广整理成文,与读者分享.
结论1如图1,过点F(0,m)任意作两条弦分别与抛物线y=ax2(a>0)交于点A,B,C,D,连结AC,BD交直线y=m于M,N两点,则点M,N关于点F对称.
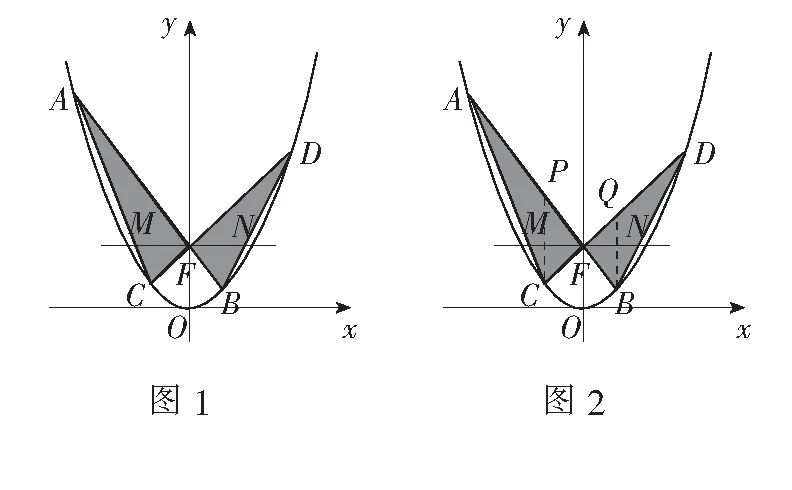
证明不妨设直线AB的方程为y=k1x+m,设点A,B,C,D的横坐标分别为xA,xB,xC,xD.
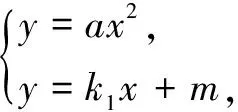
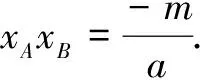

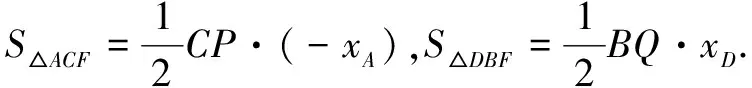


评注这种证法借助几何直观,将抛物线上点的坐标的关系显性化,不仅避免了复杂的计算,而且可以领略图形的简洁美和结论的奇异美.
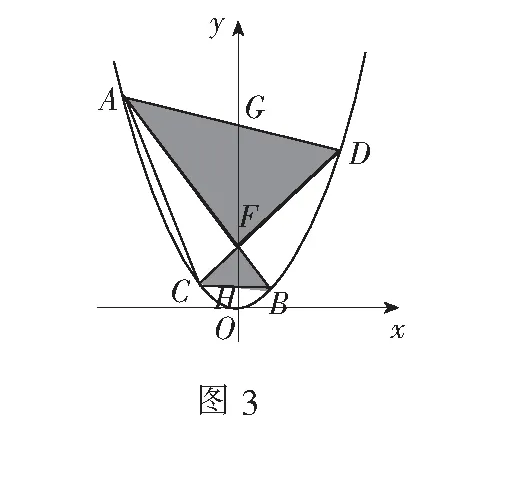
如图3,若连结AD,BC,又见蝴蝶翩翩起舞,用同样的思路继续研究,不难继续推广得到抛物线中隐含的另一个重要结论:
结论2如图3,过点F(0,m)任意作两条
弦分别与抛物线y=ax2(a>0)交于点A,B,C,D,连结AD,BC分别交y轴于G,H两点,设点A,B,C,D的横坐标分别为xA,xB,xC,xD.则有

由直线AB,CD交y轴于点F(0,m),可得到m=-axAxB=-axCxD;由直线AD,BC分别交y轴于点G,H,可得到yG=-axAxD,yH=-axBxC.


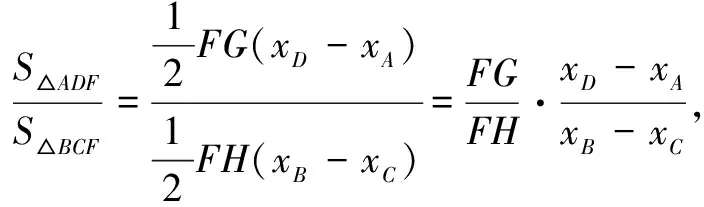
猜你喜欢
初中生学习指导·中考版(2022年3期)2022-03-25
初中生学习指导·提升版(2021年7期)2021-08-24
新课程·上旬(2020年36期)2020-12-29
初中生学习指导·中考版(2020年4期)2020-09-10
中学生数理化·七年级数学人教版(2020年4期)2020-08-10
数学教学通讯·高中版(2017年12期)2018-01-29
数学学习与研究(2017年14期)2017-07-20
今日中学生(初三版)(2013年6期)2013-07-30
数理化学习·高三版(2009年3期)2009-04-30
中学生数理化·高二版(2008年11期)2008-06-17

