巧构椭圆模型 求解另类问题
2022-11-28 08:35耿瑞照
高中数学教与学 2022年19期
耿瑞照
(山东省淄博市淄川区般阳中学, 255100)
数学建模素养是新课标确定的六大数学核心素养之一,在新课标和新高考中的地位非常重要.应用已知模型是建模素养水平最基本的要求,并且此种建模方式具有可操作性.笔者发现很多看似与椭圆无关的问题,用常规解法难度很大,但利用椭圆模型求解能够水到渠成,起到意想不到的效果.本文介绍几种常见构造(引出)椭圆模型的方式,举例说明该模型在非圆锥曲线问题中的应用.
一、借助方程引出椭圆模型
1.解无理方程
例1解方程



2.解双绝对值的不等式
例2解不等式|x-3|+|x+3|≥8.
分析本题通常用分类讨论去绝对值符号的方式求解,但运算较为麻烦.但结合例1,将|x-3|+|x+3|理解为点(x,0)到两定点(-3,0),(3,0)的距离之和,由|x-3|+|x+3|=8联想到建立椭圆模型,即可使陌生问题转化为熟悉的模型,促成问题获解.

二、借助三角形边的关系引出椭圆模型
在∆ABC中,若AB+AC=m,BC=n,其中m,n为常数,且m>n>0,则根据椭圆定义,点A的轨迹是以B,C为焦点的椭圆.借助三角形边的关系建模往往会起到意想不到的效果.当然,有些题目中给出的边的关系未必是完整的,需要我们去进一步探求;有些题目在构造椭圆时由于未知具体值,因此需用待定系数法来处理.
1.求三角形面积最值问题


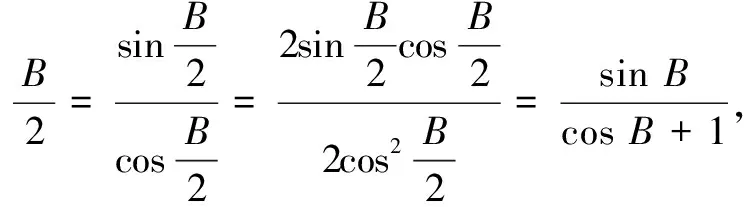

2.三角形中求值问题
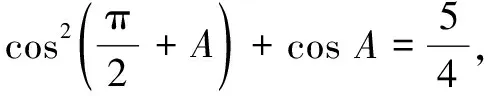

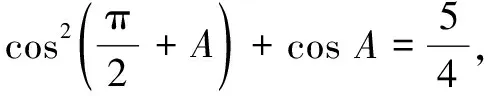

三、借助sin2α+cos2α=1引出椭圆模型
三角问题中经常借助sin2α+cos2α=1构建椭圆模型来求解(证)三角问题,特别是对于三角中的“难”题,该模型格外好用.
1.证明三角等式或不等式

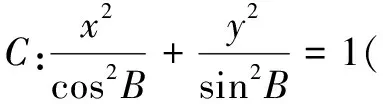


2.求三角函数的最值或值域
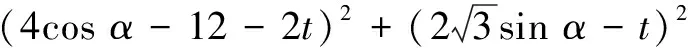
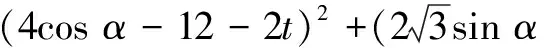



四、借助mx2+ny2=1(m,n>0且m≠n)引出椭圆模型
除了上述三种引出椭圆模型的方式外,有时也会通过代换得出mx2+ny2=1(m,n>0且m≠n)形式的式子,从而引出椭圆模型.
1.求无理函数的值域

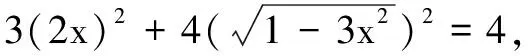

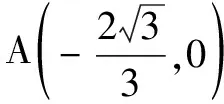
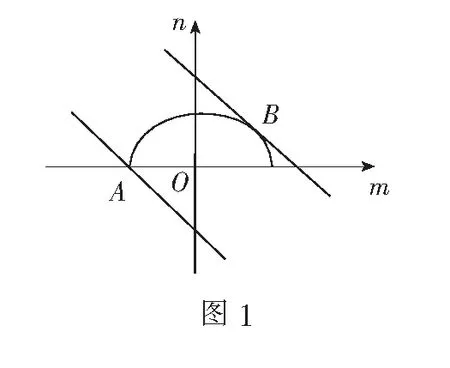

2.求二元函数的值域(最值)

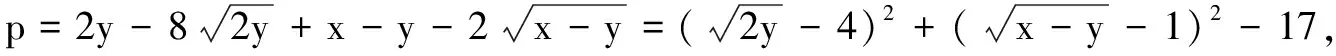
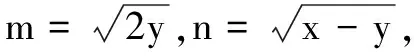
猜你喜欢
数学杂志(2022年5期)2022-12-02
中学生数理化(高中版.高二数学)(2022年3期)2022-04-26
新世纪智能(数学备考)(2021年9期)2021-11-24
中学生数理化(高中版.高二数学)(2021年12期)2021-04-26
中学生数理化(高中版.高考数学)(2021年12期)2021-03-08
新世纪智能(数学备考)(2020年9期)2021-01-04
中学生数理化(高中版.高二数学)(2020年11期)2020-12-15
语数外学习·高中版上旬(2020年10期)2020-09-10
中学生数理化(高中版.高考理化)(2020年3期)2020-05-30
新教育论坛(2019年14期)2019-09-10

