向量投影在圆锥曲线问题中的应用举隅

魏东升

(福建省厦门双十中学漳州校区，363107)

随着新课标在中学教学的实施,向量成了高中数学的重要组成部分,而其工具性也让向量问题成了高考的热点之一.根据向量数量积的定义,其几何意义是指其中一个向量的模与另一个向量在这个向量方向上投影的乘积.笔者在教学中发现,数量积中提及的向量投影的概念,在解决许多有关求最值(或求值、求范围)的各类问题中有着重要作用.本文以笔者所在学校高三模考中一道解析几何题为引例,窥视向量投影在问题求解过程中发挥的神奇功效.

一、引例与解答

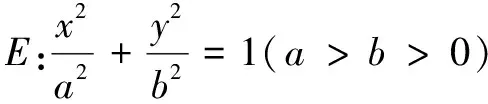
(1)求E的方程;

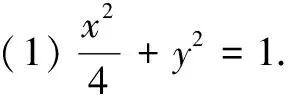
(2)解法1(常规解法)

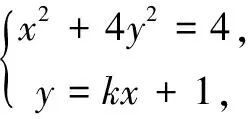
联立直线AQ与BP的方程,消去y可得

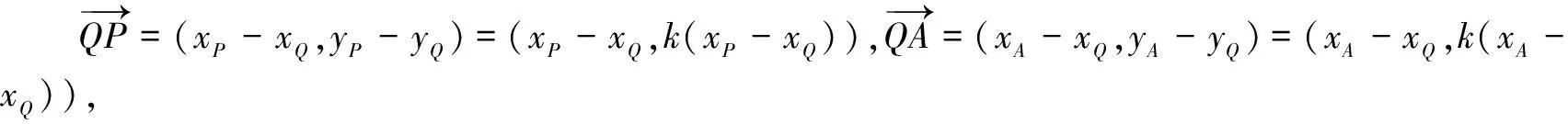
解法2(利用向量投影)

解法3(利用向量投影)

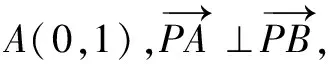
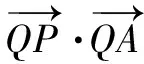
向量在对圆锥曲线中核心条件的转化上往往具备天然的优势,而向量的投影就是体现这种优势的有力证据之一.以下进一步举例说明.

二、向量投影的应用举例

1.利用投影处理定值问题

(1)求C的方程;

(2)设直线y=kx+m(m>0)交y轴于点M,交C于两不同点A,B,点N与M关于原点对称,BO⊥AN交AN于点Q.问是否存在定点M,使|NQ||NA|为定值？

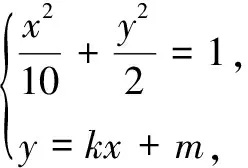
令Δ=(10km)2-4(1+5k2)(5m2-10)>0,解得m2<2+10k2.

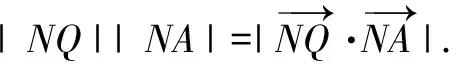
2.利用投影处理取值范围问题

(1)建立适当的坐标系,求C的方程;

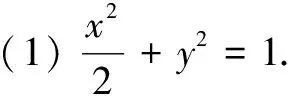
(2)如图1，因为直线AB与以OA为直径的圆的一个交点在圆O上,所以直线AB与圆O相切.

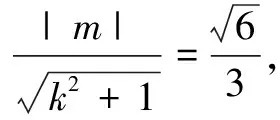
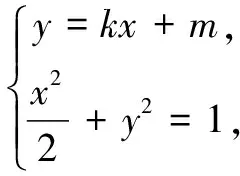
(2k2+1)x2+4kmx+2m2-2=0,

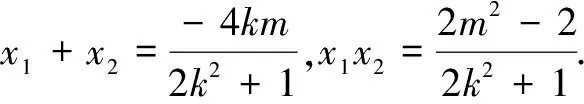
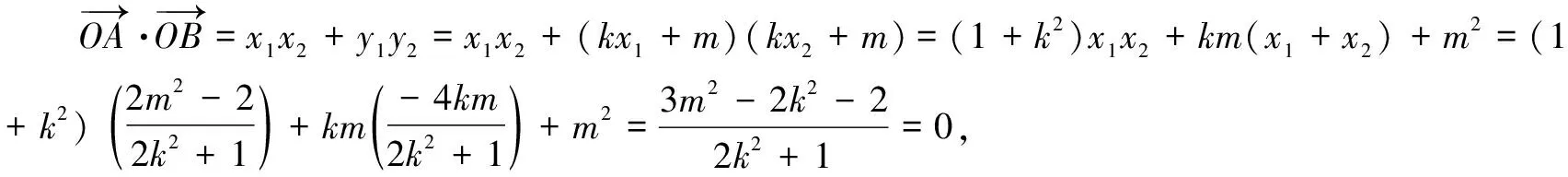
3.利用投影处理最值问题

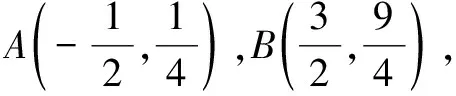
(1)求直线AP斜率的取值范围;

(2)求|PA||PQ|的最大值.

解(1)(-1,1)(过程略)

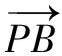
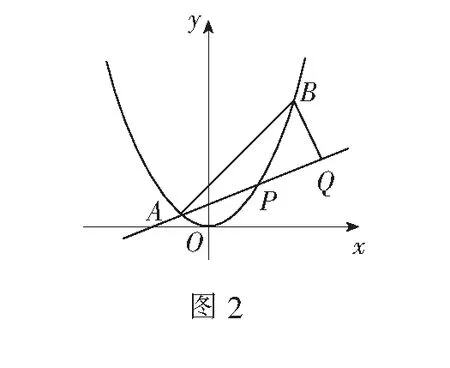
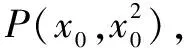
评注此题也可先求出点Q的坐标,再通过两点间距离公式分别求出|PA|和|PQ|,从而得到|PA||PQ|的表达式,但计算量较大.实际上,解析几何问题往往对学生转化与化归思想的考查提出了很高的要求,在这一点上,向量投影的作用在本题中发挥得可谓淋漓尽致.

思路决定出路,思维决定行为.通过向量投影在上述列举的部分常见问题中的应用,提醒我们在学习中应该重视对数学教材的回归,重视对数学定义的理解,重视对数学素养的渗透.唯有这样,我们对数学的学习才不至于“只见树木,不见森林”.