一个重要不等式在竞赛试题中的应用

张国治

(新疆生产建设兵团第二中学，830002)

本文从一个重要不等式出发,探源溯流,给出一类竞赛题、高考题命题的题根,给出一种高效学习数学的方法,敬请同行指正.

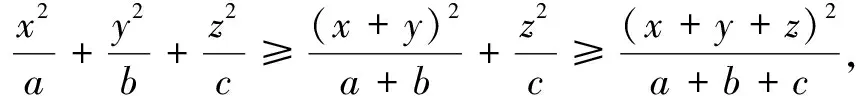
下面以竞赛题为例谈谈此不等式的应用,追本溯源,以期抛砖引玉,凸显回归题根的重要性.

一、求值

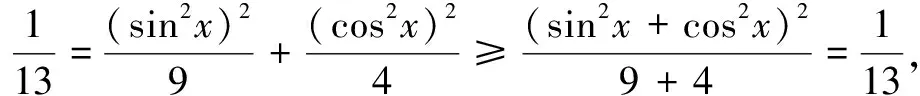
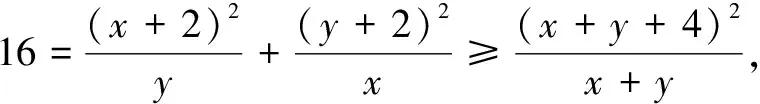
二、求最值

1.求整式的最值

例3(2018年河北省预赛题)若实数x,y,z满足x2+y2+z2=3,x+2y-2z=4,则zmax+zmin=______.

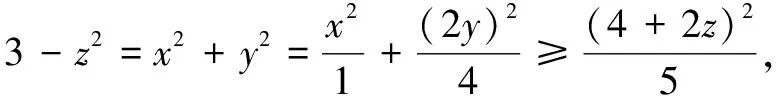
例4(2018年天津市预赛题)[3]实数x,y满足x2+y2=20,则xy+8x+y的最大值为______.

2.求无理函数的最值

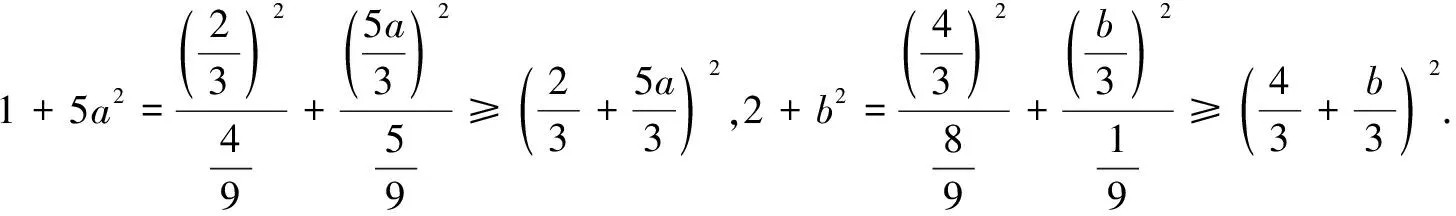
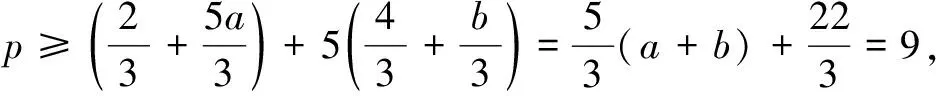
3.求分式的最值

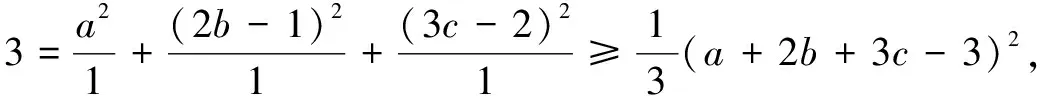
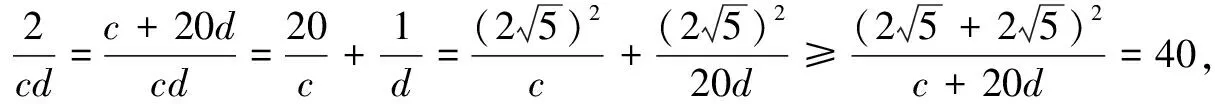
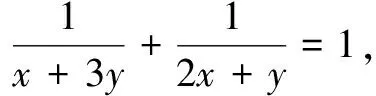
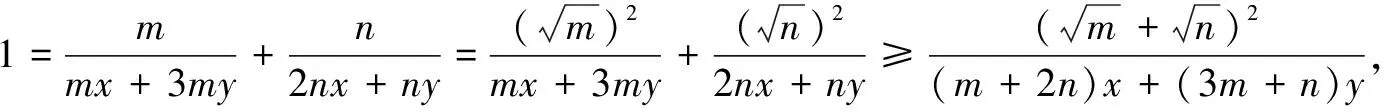
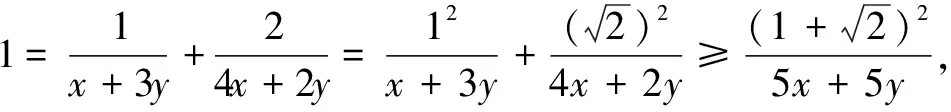
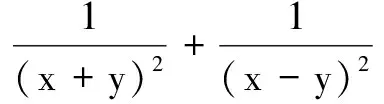
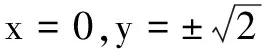
4.求三角式的最值

例10(2018年河南省高二预赛题)已知cos(α+β)=cosα+cosβ,试求cosα的最大值.

5.求数列的最值

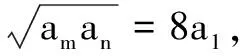
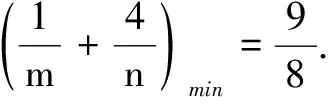
6.求几何中的最值

例12(2017年广西壮族自治区预赛题)过半径为5的球面上一点P作三条两两互相垂直的弦PA,PB,PC使得PA=2PB,则PA+PB+PC的最大值为______.

解依题意,以PA,PB,PC为相邻三条棱的长方体内接于球,长方体的体对角线为球的直径.故PA2+PB2+PC2=100,即5PB2+PC2=100.由文首结论,得

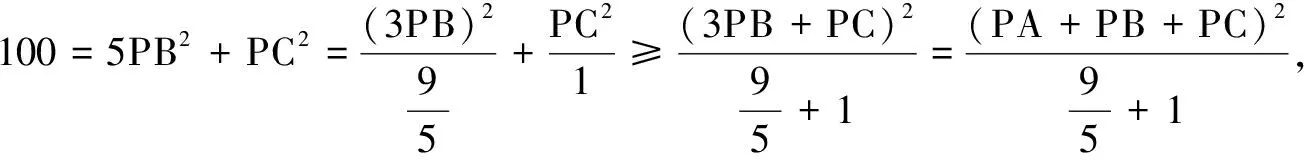
三、证明不等式

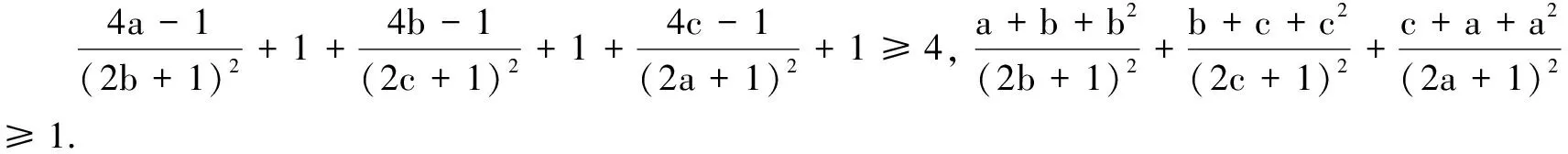
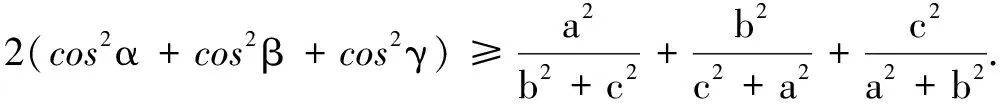
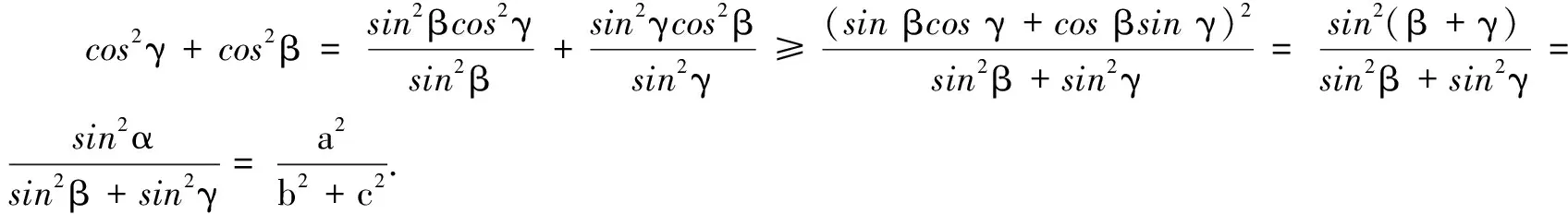
可见,研究“题根”对教学、命题和解题都有深远的意义.如果把一道数学题比作一棵大树,那么,“题根”就是它的根系,“题根”周围的知识生长点不断推广和延伸,逐渐长成了参天大树.把一个比较复杂的问题,“退”到最简单、最原始的问题,把这个最简单、最原始的问题想通了、想透了，然后再进行归纳、综合而实现质的飞跃,这是学好数学的一个诀窍,引申开来,这也是教好数学的一个诀窍.