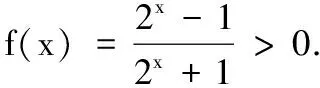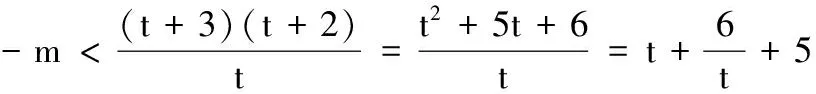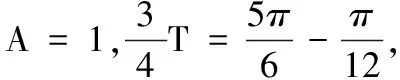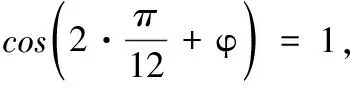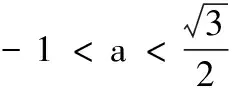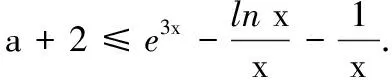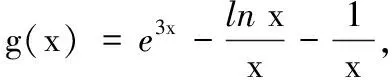高三数学综合测试

一、单项选择题(本大题共8小题，每小题5分，计40分)

1.已知集合P={x|x≥1,x∈N},Q={x|2x≤8},则P∩Q=( )

(A){x|1≤x<4}(B){x|1≤x<3}

(C){1,2} (D){1,2,3}

3.若将整个样本空间想象成一个1×1的正方形,任何事件都对应样本空间的一个子集,且事件发生的概率对应子集的面积.则如图所示的涂色部分的面积表示( )

(A)事件A发生的概率

(B)事件B发生的概率

(C)事件B不发生的条件下事件A发生的概率

(D)事件A，B同时发生的概率

4.已知实数m,n, 函数f(x)=x2+mx+n, 满足f(2)f(3)≤0, 则m2+2mn的最大值为( )

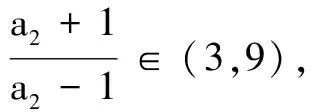
(A)a6<1 (B)a7>1

(C)a8>1 (D)a9>1

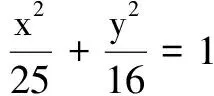
7.恰有一个实数x使得x3-ax-1=0成立,则实数a的取值范围为( )

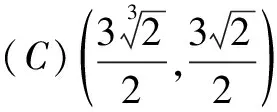
8.已知四面体D-ABC中,AC=BC=AD=BD=1,则三棱锥D-ABC体积的最大值为( )

二、多项选择题(本大题共4小题,每小题5分,计20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,有选错的得0分,部分选对的得3分)

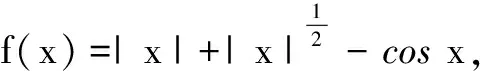
(A)f(x)是偶函数

(B)f(x)在(0,+∞)上单调递减

(C)f(x)是周期函数

(D)f(x)≥-1恒成立

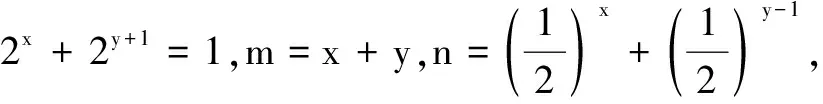
(A)x<0且y<-1

(B)m的最大值为-3

(C)n的最小值为7

(D)n·2m<2

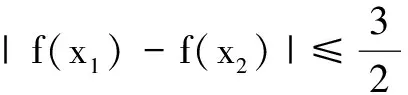
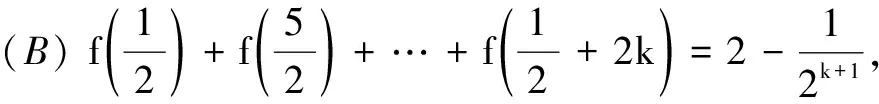
(C)f(x)=2kf(x+2k)(k∈N*)对一切x∈[0,+∞)恒成立

(D)函数y=f(x)-ln(x-1)有3个零点

(A)函数f(x)是奇函数

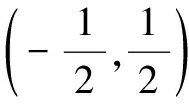
(C)函数f(x)是以2为周期的周期函数

三、填空题(本大题共4小题,每小题5分,计20分)

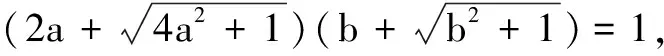
14.六名考生坐在两侧各有一条通道的同一排座位上应考,考生答完试卷的先后次序不定,且每人答完试卷后立即离开座位走出教室.则其中至少有一人交卷时为到达通道而打扰其他尚在考试的同学的概率为______.

四、解答题(本大题共6小题,计70分.解答应写出文字说明、证明过程或演算步骤)

17.(本小题满分10分)已知∆ABC的外心为O,M,N为线段AB,AC上的两点,且O恰为MN中点.

(1)证明:|AM||MB|=|AN||NC|;

(1)若点M是ED的中点,求证:CM∥平面ABE;

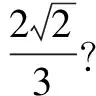
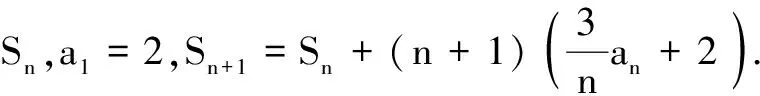
(1)求数列{an}的通项公式;

(2)若bn=an+n,试求数列{bn}的前n项和Tn.

(1)求实数a,b的值;

(2)判断f(x)的单调性,并用定义证明;

(3)当x∈[1,2]时,2+mf(x)+2x>0恒成立,求m的取值范围.

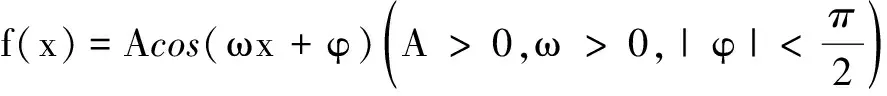
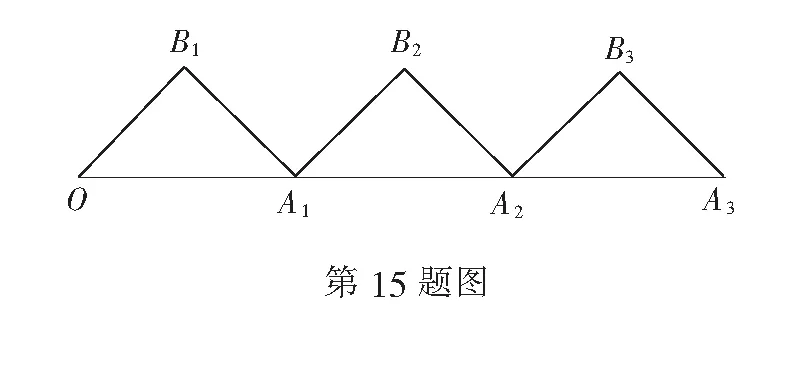
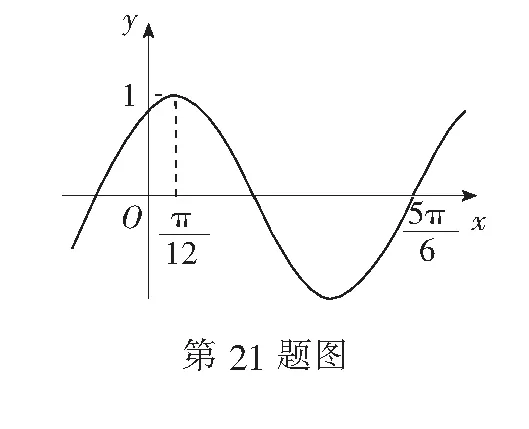
(1)求f(x)的解析式;

(3)是否存在实数a,使得函数F(x)=f(x)-a在[0,nπ](n∈N*)上恰有2021个零点？若存在,求出a和对应的n的值;若不存在,请说明理由.

22.(本小题满分12分)已知函数

f(x)=xe3x.

(1)求曲线y=f(x)在点(0,f(0))处的切线方程;

(2)若对任意的x>0,f(x)-lnx≥(a+2)x+1恒成立,求实数a的取值范围.

参考答案

一、单项选择题

1.D;2.B;3.A;4.B;5.C;

6.A;7.B;8.C.

二、多项选择题

9.AD; 10.ABD; 11.ACD; 12.ABC.

三、填空题

四、解答题

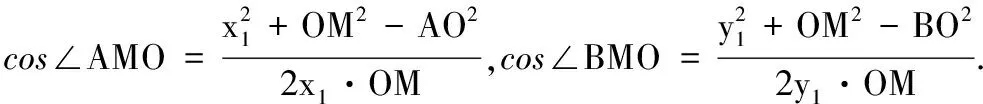
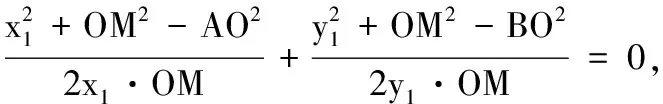
同理可知x2y2=AO2-ON2.因此x1y1=x2y2,可得|AM||MB|=|AN||NC|.

(2)由(1)知x1y1=x2y2=2,由余弦定理知

又CM⊄平面ABE,BN⊂平面ABE,所以CM∥平面ABE.

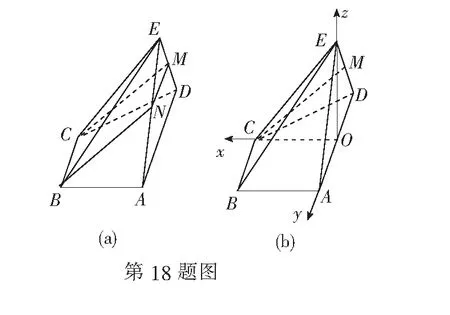
(2)取AD的中点O,连结OC,OE,易得OE⊥AD,OC⊥AD.

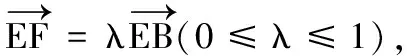
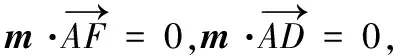
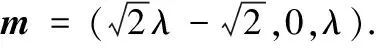
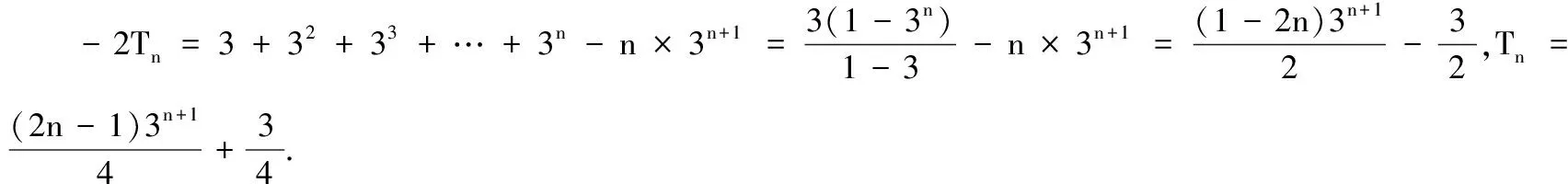
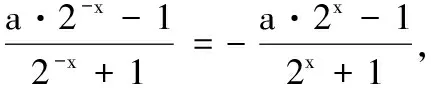
因为-a-2=-3,而定义域[-a-2,b]关于原点对称,所以b=3.

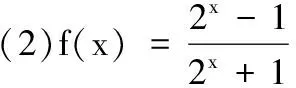
证明任取x1,x2∈[-3,3],且x1

f(x1)-f(x2)

因为-3≤x10,2x2+1>0,所以f(x1)-f(x2)<0,即f(x1)

解法1(分离变量法)

解法2(二次函数法)

综上,得m的取值范围是(-∞,-1].

当a>1或a<-1时,y=f(x)的图象与直线y=a在[0,nπ]上无交点.

当a=1或a=-1时,y=f(x)的图象与直线y=a在[0,π]仅有一个交点,故此时由y=f(x)的图象与直线y=a在[0,nπ]上恰有2 021个交点,可得n=2 021.

22.(1)因为f′(x)=(xe3x)′=e3x+3xe3x=(1+3x)e3x,所以f′(0)=1.又f(0)=0,所以曲线y=f(x)在点(0,f(0))处的切线方程为y=x.

当x∈(0,x0)时,h(x)<0,g′(x)<0,g(x)

①

②

于是由a+2≤3,得a≤1,即实数a的取值范围是(-∞,1].