探源 拓展 应用
——对一道课本向量习题的深层次研究
黄旭东
(湖北师范大学附属中学,435000)
最新人教A版数学必修二第52页习题6.4复习巩固中有这样一道习题[1]:
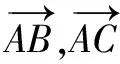
(A)三边均不相等的三角形
(B)直角三角形
(C)底边与腰不相等的等腰三角形
(D)等边三角形
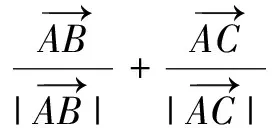
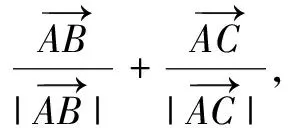
一、题源拓展
由上面习题可知,菱形的对角线为顶角平分线,则可考虑角平分线上任意角平分线向量表示,作如下拓展.

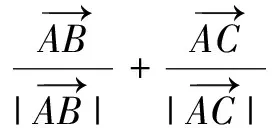
若将定理1放入三角形中,角平分线交对边于一点,则可得到λ值及分对边所成比值,即有

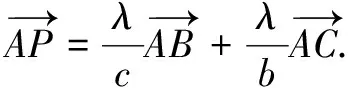

由定理2考虑三角形角平分线长,可得
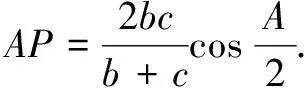
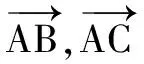
对定理3中消去三角形的内角,只建立边之间关系,可得
定理4(只与边长相关的角平分线长公式)在∆ABC中,∠A的角平分线AP交BC于点P,角A,B,C的对边分别为a,b,c,则AP2=AB·AC-BP·PC.
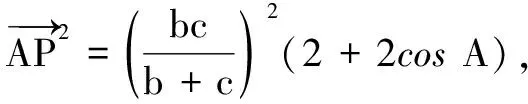
若三角形的一个内角是另一内角的2倍,不妨称之为倍角三角形.易得此类特殊三角形的边之间具有如下关系.
定理5(倍角三角形的性质)在∆ABC中,∠A=2∠B,角A,B,C的对边分别为a,b,c,则有a2=b(b+c).

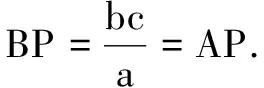
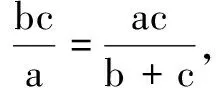
二、角平分线性质应用举例
1.角平分线广义向量形式的应用





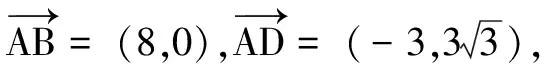

2.三角形中角平分线向量形式的应用


例4在∆ABC中,内角A,B,C所对的边分别为a,b,c,sinA=2sinB.
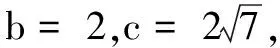
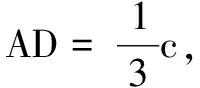
解(1)略.
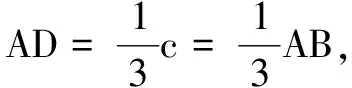
3.边角相关的三角形内角平分线长公式的应用
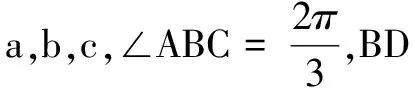
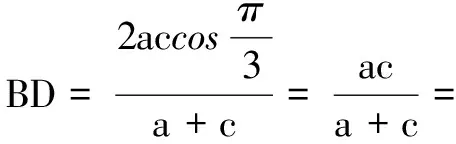
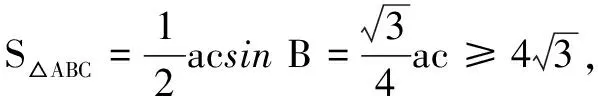
例6已知∆ABC中, 角A,B,C所对的边分别为a,b,c,bcosC=a, 点M在线段AB上, 且∠ACM=∠BCM.若b=6CM=6,则cos∠BCM=( )
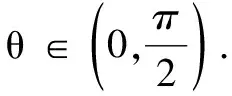
4.利用边关系求内角平分线长
例7在∆ABC中,∠BAC的AD角平分线交BC于点D,∆ABD面积是∆ADC面积的2倍.



又由c=2b,得AB=2AC.由定理4知AD2=AB·AC-BD·DC,即1=2AC2-1,所以AC=1.
例8在∆ABC中,AB=5,AC=7,BC=6,∠A的平分线交边BC于点D,则AD=______.
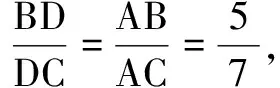
5.解倍角三角形问题
例9记∆ABC的内角A,B,C的对边分别为a,b,c,已知a,b,c是三个连续的正整数,且a 解由C=2A及定理5,得c2=a(a+b).不妨设b=1+a,c=a+2,则(a+2)2=a[a+(a+1)],即a2-3a-4=0,由此解得a=4. 例10在∆ABC中,角A,B,C的对边分别为a,b,c,若b=2,acosB-2cosA=2. (1)求证:A=2B; (2)若∆ABC的面积等于λsinC,求λ的取值范围. 解(1)由条件得acosB-bcosA=b,由正弦定理可得sinAcosB-sinBcosA=sinB,即sin(A-B)=sinB,而A,B∈(0,π),故A-B=B,得A=2B. (2)由A=2B及定理5,知a2=b(b+c)=4+2c. 由0 解得2 课本中例题或习题很多具有典型的意义,利用例题或习题进行题组训练、变式训练、拓展训练,挖掘题源与变式,可有效提高教学效率,提升学生的数学核心素养,培养学生的创新精神.因此在平时教学过程中,不能一味只搞题海战术,应引导学生重视教材与课本,重视例题与习题的拓展与延伸,回归教材,才是教学的本源与根本.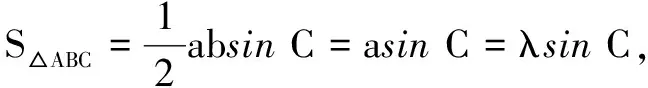
三、结束语

