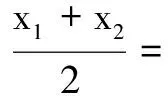利用函数对称性与周期性的关系解题
杨 婷
(甘肃省庆阳市北京师范大学庆阳附属学校,745200)
函数图象的对称性和周期性是函数的两个重要性质,许多函数问题常常需要利用两个性质的关系来求解.本文先归纳、证明这两个性质关系的几个基本结论,再举例说明这些结论在求解相关问题中的应用.
一、基本结论
结论1若函数y=f(x)的图象分别关于两条直线x=a,x=b(a≠b)对称,则函数y=f(x)是周期函数,且T=2|a-b|为y=f(x)的一个周期.
结论2若函数y=f(x)的图象分别关于两点A(a,0),B(b,0)(a≠b)对称,则y=f(x)是周期函数,且T=2|a-b|为y=f(x)的一个周期.
结论3如果函数y=f(x)的图象关于点A(a,0)和直线x=b(a≠b)对称,则函数y=f(x)是周期函数,且T=4|a-b|为y=f(x)的一个周期.
几个结论的证明具有一定的相似性,下面仅以结论3为例,给出证明.
因为y=f(x)的图象关于点A(a,0)对称,设P(x1,y1),Q(x2,y2)为y=f(x)上任意一对对称点,则x1+x2=2a且y1+y2=0.所以y2=-y1,即f(x2)=-f(x1),亦即f(2a-x1)=-f(x1).由x1的任意性,可知f(x)=-f(2a-x)对定义域内的所有x成立.
又因为函数y=f(x)的图象关于直线x=b对称,同理可知f(x)=f(2b-x)对定义域内的所有x成立.
于是,对定义域内的所有x,恒有f(2b-x)=-f(2a-x).
所以f[2b-(2a-x)]=-f[2a-(2a-x)]=-f(x),即f[2(b-a)+x)]=-f(x).进而f{2(b-a)+[2(b-a)+x]}=-f[2(b-a)+x]=f(x).即f[4(b-a)+x]=f(x).可见y=f(x)是周期函数,且T=4|a-b|为f(x)的一个周期.
二、应用举例
1.求函数值
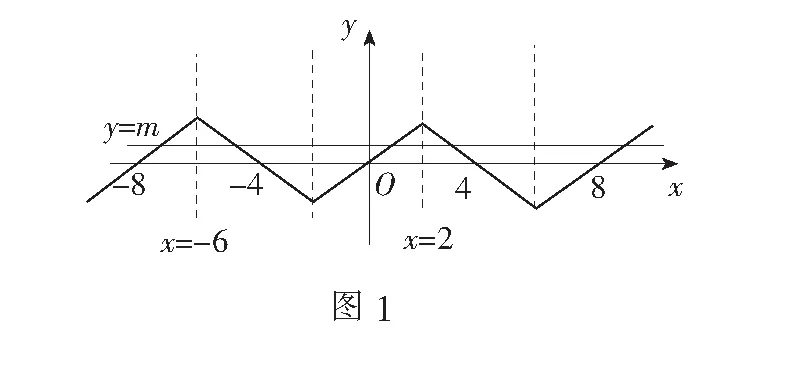
例1已知f(x)为R上的奇函数,并且f(x)+f(2-x)=0,当-1 解由f(x)为R上的奇函数,得f(x)图象关于点(0,0)对称;又由f(x)+f(2-x)=0,得f(2-x)=-f(x),即f(x)图象关于点(1,0)对称.由结论2,可知y=f(x)是周期函数,且以T=2|1-0|=2为函数f(x)的一个周期. 例2已知定义域为R的可导函数y=f(x)满足f(4-x)=f(x),且f(8-x)=f(x),则曲线y=f(x)在x=2 022处的切线的斜率为( ) (A)2 022 (B)2 021 (C)1 (D)0 解由f(4-x)=f(x),可知f(x)图象关于直线x=2对称;由f(8-x)=f(x),可知f(x)图象关于直线x=4对称.所以由结论1可知函数f(x)和它的导函数f′(x)都是R上的周期函数,且T=2|2-4|=4为它们的一个周期. 因为f(x)图象关于直线x=2对称,所以f′(2)=0.又2 022=505×4+2,于是f′(2 022)=f′(2)=0.故选D. 2.比较大小 例3已知定义在R上的函数f(x)满足:①f(-x)+f(x)=0;② 函数f(x)的图象关于直线x=2对称;③ 在区间[0,2]上是增函数.则( ) (A)f(18) (B)f(5) (C)f(5) (D)f(18) 解由条件① 知f(x)为奇函数,所以f(x)的图象关于原点(0,0)对称. 又函数f(x)的图象关于直线x=2对称,由结论3可知y=f(x)是周期函数,且T=4|0-2|=8为f(x)的一个周期. 由① ③ 知f(x)在[-2,2]是增函数. 于是f(18)=f(2),f(-32)=f(0),f(5)=f(-1).结合函数f(x)在[-2,2]的单调性,可得f(-1) 3.求解方程问题 例4已知函数f(x)是定义在R上的奇函数,满足f(x-4)=-f(x),且在区间[0,2]是增函数.若方程f(x)=m(m>0)在区间[-8,8]上有四个不同的根x1,x2,x3,x4,则x1+x2+x3+x4=( ) (A)-12 (B)-8 (C)-4 (D)4 解因为f(x)为R上的奇函数,所以f(x)图象关于点(0,0)对称. 因为f(x-4)=-f(x),即f(4-x)=f(x),所以f(x)的图象关于直线x=2对称. 所以根据结论3可知函数y=f(x)是周期函数,且T=4|0-2|=8为函数y=f(x)的一个周期. 又因为f(x)在[0,2]是增函数,所以f(x)在[-2,0]也是增函数.如此不难画出f(x)的草图,如图1. 同理x3+x4=4.所以x1+x2+x3+x4=-12+4=-8.故选B. 4.综合应用 例5已知函数f(x)满足:当x∈(-∞,+∞)时,f(2-x)=f(2+x)且f(7-x)=f(7+x),在区间[0,7]只有f(1)=f(3)=0. (1)试判断f(x)的奇偶性; (2)试求方程f(x)=0在[-2 022,2 022]上的根的个数,并证明你的结论. 解由f(2-x)=f(2+x),可得f(x)=f(4-x),所以f(x)图象关于直线x=2对称. 由f(7-x)=f(7+x),可得f(x)=f(14-x),f(x)图象关于直线x=7对称. 所以由结论1可知y=f(x)是周期函数,且T=2|2-7|=10为f(x)的一个周期. (1)由于在闭区间[0,7]只有f(1)=f(3)=0,所以f(-3)=f(7)≠0.显然f(-3)≠f(3),且f(-3)≠-f(3),故f(x)是非奇非偶函数. (2)由f(1)=f(3)=0,f(x)=f(4-x)及f(x)周期为10,得f(11)=f(13)=f(-9)=f(-7)=0,可知f(x)=0在区间[0,10]及[-10,0]各有两个根. 因此,由2 022=202×10+2,可得到函数f(x)=0在区间[0,2 022]有405个根,在区间[-2 022,0]有404个根.故在[-2 022,2 022]的所有根的个数为809个. 评注本题的一个重要“点”是给出了两个类似的函数等式.抓住这个“点”联想到函数的对称性,由结论1可知函数f(x)一定是周期函数.从周期出发,我们是通过思考两点求解的:(1)借助f(1)=f(3)=0求出一些函数值,由此可发现奇偶性;(2)求出一个周期上方程f(x)=0根的个数,再由周期性得出在区间[-2 022,2 022]上的所有根的个数.