“一题一课”视角下的初中数学习题课初探
——基于圆综合复习题的教学实践
陈 琦
(海曙区储能学校,浙江 宁波 315010)
1 现状与思考
1.1 现状审视
习题课是初中数学复习课的重要课型.在传统的数学习题讲评课中,大多数教师是以复习概念、讲解习题为主;选择的例题多而散,针对性不强,缺乏层次感;学生课堂参与度不高,无法真正化为自己的知识.应试教育缺失研究与实践,缺乏探究与创新,从而直接导致学生出现机械记忆、套用公式等浅层次学习的现象.
1.2 背景简述
“一题一课”逐渐成为一种新型的习题课,它以切口小、内容精、方法多的特点频繁出现在课堂教学评比和平时的复习课教学中,吸引了广大数学教师.“一题一课”,本质上是利用“一题”串联多内容、系统化的复习课教学形式,彰显数学学习内容的整体性和关联性.
笔者所在区连续几届教坛新秀评比都采用“一题一课”的课堂教学评价模式,2022年的课题是以提供的试题为基本素材进行专题复习教学.
1.2.1 素材

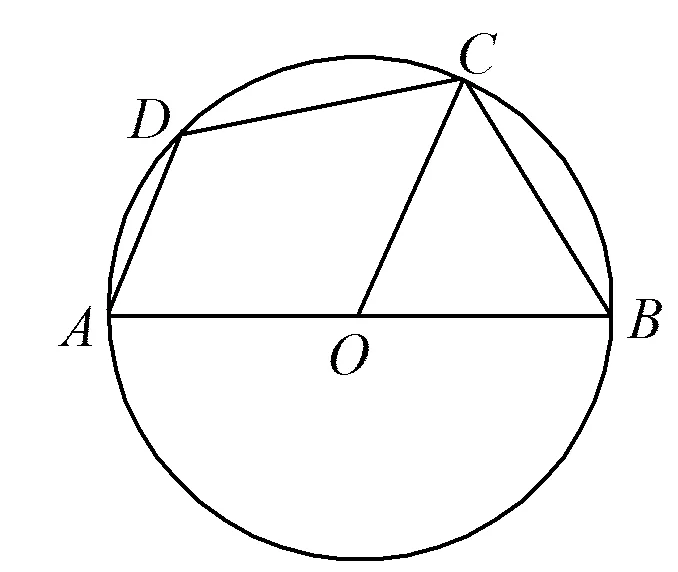
图1
1)求证:AD∥OC;
2)求y关于x的函数关系式;
3)求四边形ABCD周长的最大值.
1.2.2 要求
1)充分挖掘素材的知识点,思考问题,理清思路,设计课堂教学互动.
2)本次评价授课对象为初三(九年级)学生.授课时间40分钟.
1.3 改进与思考
针对目前习题课的现状,我们需要解决当下数学课堂中普遍存在的知识碎片化、认识表层化及方法单一化等问题.把浅层学习转变为学生的系统化思维活动,让学生积极参与、深度思考,达到激活知识、自我建构数学知识体系的目的.
高品质习题课重在优化数学任务的设计.本文通过教师A设计的这节比赛课,对以上背景材料进行分析,抓住圆的综合知识的核心,呈现出有梯度的教学环节,努力培养学生的发散性思维.教师A设计的流程图如下:

2 基于活动化的教学流程设计
2.1 基本教学流程
活动1识图.

预设1CD=BC(等弧所对的弦相等).
预设2∠A=∠COB(圆周角定理).
预设3AD∥OC(同位角相等,两直线平行).
预设4∠B+∠D=180°,或∠A+∠BCD=180°(圆内接四边形定理).
设计意图低起点入课,人人都能积极参与课堂,复习圆中基本定理,如圆周角定理、圆内接四边形定理等.既用实例复习圆中的核心定理,又为后续的证明提供依据.
活动2探图.
在初始图形的基础上,如图2,再联结图形中的一条线段,你能得到哪些新的结论?

图2
预设1联结BD,得到∠ADB=90°,OC垂直平分BD(垂径定理).
预设2联结AC,得到∠ACB=90°,∠DAC=∠CAB=∠ACO,从而得到AD∥OC(圆周角定理).
预设3联结OD,得到∠COD=∠COB,也可以推导出AD∥OC(圆心角定理).
设计意图学生通过添加不同的辅助线,进一步巩固圆中的核心定理,如垂径定理、圆心角定理等,不断完善圆定理的复习内容.课堂因学生的活动而精彩.
活动3品图.
在初始图形的基础上,如图3,延长AD,BC交于点E,你能得到哪些新的结论?联结AC,你还能得到哪些新的结论?

图3
预设1CE=CB(中位线的逆定理).
预设2△EDC∽△EAB,△COB∽△EAB,△EDC∽△COB.
预设3联结AC,得AC是∠DAB的平分线,也是边BE上的高线,易证△ACE≌△ABC(ASA),得CE=CB,AE=AB,△ABE是等腰三角形.
预设4再联结BD,则
设计意图在图形外作辅助线,学生较难想到,教师示范添线,再现“新大陆”.发现图形中蕴涵着线段相等、角相等、面积相等,还有相似三角形、全等三角形等,这些都为后续求四边形ABCD周长的最大值提供了不同的方法和思路.
活动4读图.


图4
1)当AD变化时,CD是否变化?你能确定y与x的取值范围吗?
2)请你添加一个y的值,并求出此时x的取值.
3)请用尽可能多的方法求y关于x的函数表达式.
预设当AD变化时,CD也随之变化,且

OC⊥BD,DF=BF.
又OA=OB,从而
在Rt△CFB中,
BC2-CF2=BF2.
在Rt△OFB中,
OB2-OF2=BF2,
于是
OB2-OF2=BC2-CF2,
即
亦即
设计意图赋予变量,引导学生发现AD与CD之间的关系,从特殊到一般,为后续求四边形ABCD周长的最大值做铺垫,同时利用不同的构造,积极引导学生探究一题多解,使圆的复习层层深入,与所学的几何知识多方位联系,真正拓展了学生的思维.
活动5用图.
如图1,四边形ABCD是⊙O的内接四边形,AB是直径,点C为BD的中点.已知AB=10,CD=x,AD=y,请求出四边形ABCD周长的最大值.
周长=AB+AD+CD+BC=10+y+2x

设计意图建立函数模型,求解几何最值问题,有了前面的探究过程,这一环节显得顺理成章,发展了学生数学建模的核心素养,体现了函数的应用价值.
2.2 圆综合题解题拓展教学流程
在几何学的教学实践中,往往一题会存在多种不同的解题思路,但殊途同归,能得到相同的结果.在本节圆的“一题一课”教学中,为拓展解题思路,开阔学生的解题视野,教师设计了如下拓展题教学.

拓展思路通常可利用平行线的判定证明平行,如寻求同位角和内错角的等量关系等.
方法1利用垂径定理证明OC⊥BD.由于AB为直径,因此可证明∠ADB=90°.
方法2联结AC,利用弧相等、圆周角相等证明∠DAC=∠CAB.再根据OA=OC,得
∠CAB=∠ACO=∠DAC,
得
AD∥OC.
方法3利用圆心角和圆周角与弧的关系.由
从而
AD∥OC.
拓展问题2如图5,四边形ABCD是⊙O的内接四边形,AB是直径,点C为BD的中点.已知AB=10,CD=x,AD=y,请求出四边形ABCD周长的最大值.

图5
拓展思路1)本题目标是建立相关的数学模型,通过模型讨论周长的最大值问题;
2)通过以前学习的知识,知道这个数学模型是二次函数最值问题;
3)围绕周长关系式C=10+2x+y,将式中多个变量转化成单变量;
4)在数学建模过程中,关键是要找到x与y的关联和解决这些关联的途径和方法;
5)方法:通过作辅助线,根据已知条件构思角、边、几何图形,结合几何图形的性质、定理进行推导.
方法1如图5,延长CO交圆于点E,联结BE.易证
△CMB∽△CBE,
得
CB2=CM·CE,
即
方法2如图6,延长BC,AD交于点E.易证

图6 图7
△ECD∽△EAB,
得
EC·EB=ED·EA.
因为CD=CB=x,∠EDB=90°,易证
CD=CB=CE=x,
∠EDC=∠E=∠ABE,AE=AB=10,
所以
x·2x=10(10-y).
方法3利用面积相等(如图7).
从而
方法4如图8,将△ADC绕点C逆时针旋转,使CD旋转到CB.利用射影定理,得

图8 图9
CB2=MB·AB,
从而得出结论.
方法5如图9,过点C作CE⊥AD交AD的延长线于点E,CF⊥AB.由△EDC≌△CFB,△ACE≌△ACF,可设DE=BF=a,a+y=10-a,再由射影定理得CB2=BF·AB,从而得出结论.
3 教学思考
3.1 “一题一课”设计要以题干为依据,挖掘题目本身的知识点
“一题”即指问题的题干不变,依托同一个问题背景或情境,从某些重要的知识、方法或模型运用等为切入点,将平时学习中割裂的、碎片化的知识有效联结起来,系统架构,整体设计“一课”,使学生由此及彼,达到知识与方法的融会贯通[1].
本课的设计侧重点是圆等几何知识的复习,素材提供了这道几何题本身所蕴涵的丰富的几何知识点及其应用.我们要以题干为依据,从一个基本图形出发,激活学生已有的知识积累,然后逐渐添线,变换图形,赋予图形不同的情境,让学生理解变式图形的基本要素之间的关系,从而找到解决问题的核心知识点与方法.通过学习,学生在课堂中对圆、三角形等几何核心知识进行了梳理,同时又体会到其在函数领域的应用价值.
3.2 “一题一课”设计要从学生的认知规律出发,为学生搭建合适的台阶
波利亚曾说过:“一个专心、认真备课的教师能够拿出一道有意义但不太复杂的题目,帮助学生挖掘问题的各个方面,使得通过这道题,就好像通过一道门户,把学生引入一个完整的理论领域.”[2]“一题一课”设计的探究互动应符合学生的认知规律,遵循思维的最近发展区.教师要善于为学生搭建合适的台阶,引导学生学会审题和分析,把题目中的各个知识点串成知识线,进而融成知识面.设计围绕素材图形,每个问题的提出由浅入深,前后呼应.本案例通过添加辅助线、复习圆中的基本知识,强化对知识的深度理解.开放性问题引导学生发现y和x之间存在的关系,为得出y关于x的函数关系式提供方法,从特殊到一般,很好地突破了本课的难点,最后顺理成章地解决四边形ABCD周长的最大值问题.这样的设计,一气呵成.
坚持以学生为主体,通过设计有阶梯式的问题,启迪学生积极思考,主动去透视课堂,提炼解题策略,渗透数学思想,挖掘数学本质,让学生真正成为课堂的主人,彰显“一题一课”的价值.
3.3 “一题一课”教学中教师要善于“借题发挥”,引导学生“一题多解”
“一题多解”是数学习题课教学的重要形式,是培养学生思维品质的有效途径.教师在解题教学中注重“一题多解”,有利于学生深度认识数学知识的本质,探寻知识之间的区别与联系,掌握解决问题的一般规律,克服思维定势,培养创造性思维能力[3].
在“一题多解”的教学过程中,学生的方法很多,本案例中如果教师没有耐着性子倾听学生的各种解法,就看不到多种解法的思维火花,也就不会有随后对各种解法的探究与比较,这就造成教育价值的流失.教师不但要学会倾听,更要善于总结归类,要帮助学生分清是不是一类方法,如在证明平行中,拓展方法1和拓展方法3都用到了同位角的关系,可以总结为一种思路;又如求y关于x的函数关系中,拓展方法1和拓展方法2都利用相似建立边之间的关系,但是证明相似的思路不一样,拓展方法1使用的是垂径定理,拓展方法2使用的是直角三角形的性质和圆内接四边形的性质;拓展方法3利用面积相等;拓展方法4和拓展方法5都是通过构造全等三角形,利用射影定理找出x,y之间的等量关系.所有的方法都可以归结为求y关于x的函数关系式,这就是方程的数学思想.加强学生数学学科核心素养的培养,就需要教师适时地总结、提炼数学思想方法,让学生“会一题,得一法,通一类”.
3.4 “一题一课”的教学要重视问题化和互动化,引导学生深度参与课堂教学
托尔斯泰曾说:“成功的教学所需要的不是强制,而是激发学生的兴趣.”浓厚的学习兴趣,可以使学生产生强烈的求知欲、敏锐的思维力、丰富的想象力以及迫切探求新知识和新问题的推动力.基于此,对于习题课的教学,教师需要适时后退,促使学生主动地深度参与课堂教学.
在本案例中,教师在设计教学内容时充分考虑了问题化和互动化,通过问题串联知识点,在活动1~活动5中活用素材.学生先通过添加辅助线改变问题的情境,然后以问题为导线由浅入深,各个层次的学生都能经历数学观察、操作、归纳、验证、问题解决等数学学习过程,获得了研究数学问题的经验,凸显了以全体学生为主体的数学课堂.

