对一类新知阅读题的探究与思考

郝文华

(北京师范大学盐城附属学校，江苏 盐城 224007)

所谓新知阅读题，是指通过阅读理解题目中提供的相关材料，获取新知(包括新定义、新结论、新公式等)，并要求迁移运用的一类数学问题[1].这也是新高考背景下，高三各类试卷中常见的一类试题.这类题目往往对学生的数学阅读能力、知识的迁移运用及学习与创新能力有较高的要求，也是评估学生综合学力的一个有效载体，非常契合当前新高考的选拔功能.新知阅读题在命题形式上涉及选择、填空及解答这3种形式，但由于具有一定的综合性和较强的灵活性，一般题号比较靠后，多数为“压轴”试题.

1 直接定义(规定)型问题

此类问题一般先给出某个新概念或某种运算规则，要求利用这个新的定义或规则去解决相关问题.对于问题的解决，有的是直接套用，有的还需拓展延伸、灵活应用，主要考查学生的阅读理解、探究创新及知识的迁移运用能力.

例1对于函数f(x)，一次函数g(x)=ax+b，若f(x)≤g(x)恒成立，则称g(x)为函数f(x)的一个“线性覆盖函数”．若函数g(x)=x-1是函数f(x)=sin 2x-aex(其中x≥0)的一个“线性覆盖函数”，则实数a的取值范围是( )

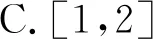
分析由“线性覆盖函数”的规定可知sin 2x-aex≤x-1在[0，+∞)上恒成立，将x=0代入可得

a≥1，

故

aex≥ex.

令h(x)=ex-sin 2x+x-1，其中x≥0,则

h′(x)=ex+1-2cos 2x≥2-2cos 2x≥0，

从而h(x)在[0，+∞)上单调递增，又h(0)=0，于是h(x)≥0，因此当a≥1时，f(x)≤g(x)恒成立.故选B.

评注本题通过给出“线性覆盖函数”这一新知识点的定义，引导考生利用定义解决一个恒成立问题，考查了学生的阅读理解能力及对新知的迁移应用能力.考生只要弄清“什么是线性覆盖函数”，就可迅速找到解题的“入手点”，但前期思路的形成，不代表后面能够顺利解出，还需了解恒成立问题的一般处理性策略.

( )

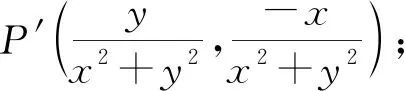
A.若点A的“伴随点”是点A′，则点A′的“伴随点”是点A

B.单位圆的“伴随曲线”是它自身

C.若曲线C关于x轴对称，则其“伴随曲线”C′关于y轴对称

D.一条直线的“伴随曲线”是一条直线

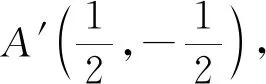
对于选项B，设单位圆上任一点的坐标为P(cosx,sinx)，其“伴随点”为P′(sinx,-cosx)仍在单位圆上，故选项B正确.

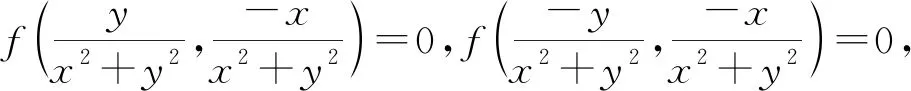
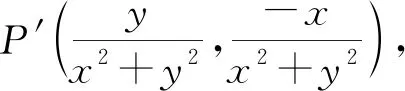
从而

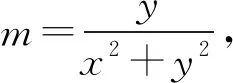
从而点P′的轨迹是圆，故选项D错误.正确答案为B和C．

评注本题题干不长，但信息量较大，相当于给出了“伴随点”及“伴随曲线”两个新概念，且较为抽象，对考生的阅读理解能力及灵活处理“对称性”问题的能力要求较高.再加上本题有多个选项符合要求，无形中又增加了题目难度.

2 以数学史(数学文化)为背景的新知阅读题

此类问题常以数学名人与名著、猜想与结论、成果与发现、故事与时事、名题与趣题等为取材背景，以数学知识和能力为载体，以对数学素养的考查为目的，在各地模拟及高考中出现的频率逐渐升高，其重要性与必要性不言而喻.这是新高考的一大显性特点，也为中学数学教学提供了一个良好的导向.

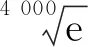
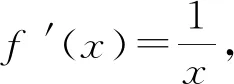
y=x-1.

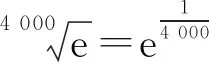
即

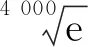
例4由倍角公式cos 2x=2cos2x-1，知cos 2x可以表示为cosx的二次多项式．一般地，存在一个n次多项式Pn(t)，使得cosnx=Pn(cosx)，这些多项式Pn(t)称为切比雪夫多项式．例如cos 2x=P2(cosx)=2cos2x-1，记作P2(t)=2t2-1．利用P3(t)求得sin 18°=

( )

分析因为

cos 3x=cos(2x+x)=cos 2xcosx-sin 2xsinx

=(2cos2x-1)cosx-2sinxcosxsinx

=4cos3x-3cosx,

所以

cos 54°=4cos318°-3cos 18°，

即

sin 36°=4cos318°-3cos 18°，

从而

2sin 18°cos 18°=4cos318°-3cos 18°，

于是

2sin 18°=4(1-sin218°)-3,

即

4sin218°+2sin 18°-1=0，

解得

评注本题利用切比雪夫多项式的结构特点，结合三角恒等变换公式，求出sin 18°的值.在这个过程中，切比雪夫多项式提示了三角变换的方式，为引出关于sin 18°的一元二次方程指明了方向.可以说，题目中所提供的切比雪夫多项式的结构，本身就是一种解决问题的方法.以数学史(数学文化)为背景的新知阅读题在近年新高考试卷中也时常出现，如2020年全国数学新高考中的“日晷”问题、2022年全国数学新高考中的“中国古代建筑”问题等.

3 基于概念(定理、公式、结论等)延伸型的新知阅读题

还有一类新知阅读问题，其命题背景并非来源于数学史，而是从学生熟悉的基本概念、定理、定义、公式、结论等出发，要求在理解知识的产生、发展过程的基础上，对概念进行延伸或推广，并用此来解决一些较为灵活的数学问题.例如，定义一种新的向量运算：a⊗b=|a|·|b|·sin ，类比向量数量积的性质，探究上述运算的性质.此类问题往往对学生的理解能力、创新意识及数学的应用能力要求较高.

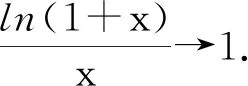
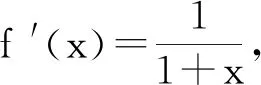
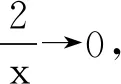
即

亦即

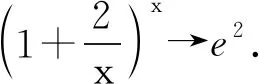
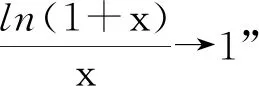
例6无穷符号∞在数学中是一个重要的符号，该符号的引入为微积分和集合论的研究带来了便利.某校在一次数学活动中以无穷符号为创意来源，设计了如图1所示的活动标志，该标志由两个半径分别为15和20的实心小球相交而成，球心距O1O2=25，则该标志的体积为______.

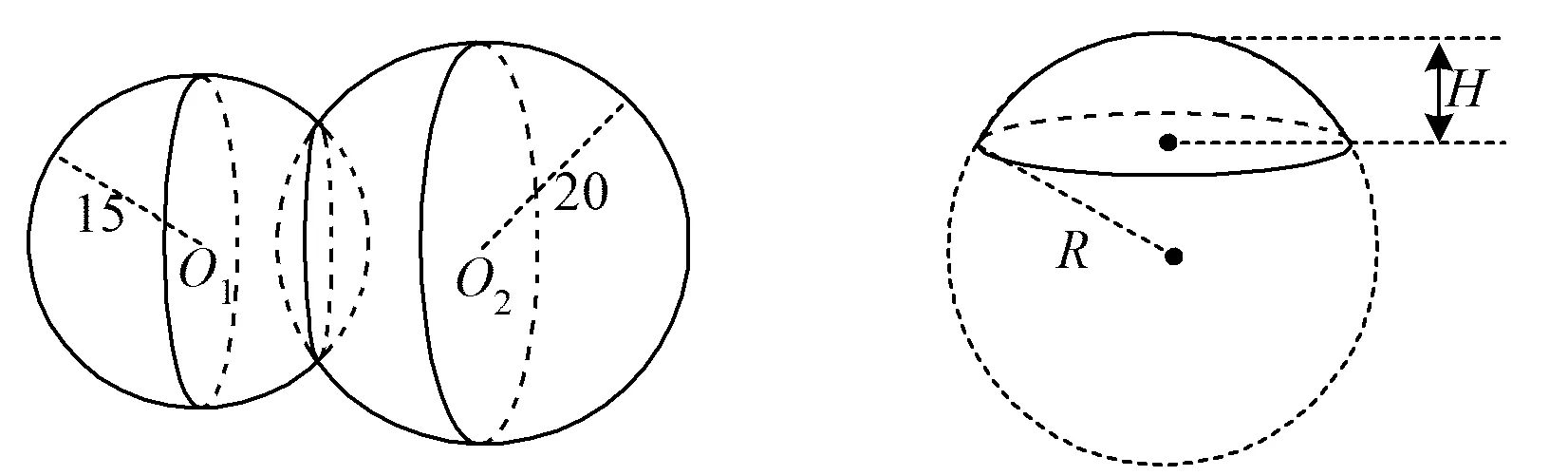
图1 图2

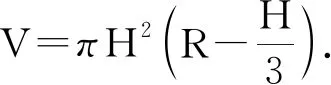
分析记两球面的交线为⊙O，其大圆截面如图3所示，则

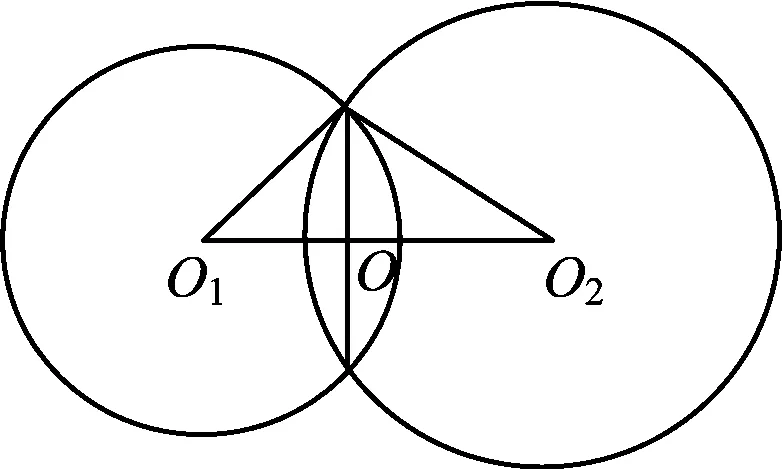
图3

152-O1O2=202-O2O2，

且

OO1+OO2=25，

解得OO1=9，OO2=16，

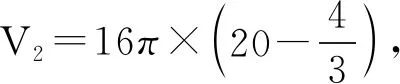
=14 400π.

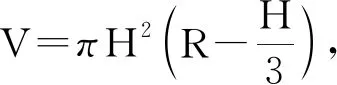
新知阅读类试题是考查学生数学阅读能力的一类重要题型.由以上例题可以看出，此类问题的解决过程基本遵循两个操作步骤:一是需要阅读相关新知材料，理解其想要表达的真正内涵;二是迁移运用新知来解决具体问题.毋庸置疑，新知阅读题对于提升学生的阅读理解能力和对知识的迁移应用能力有着较高的学习价值，这也是发展学生关键能力与发挥考试选拔功能的重要题型，因此应引起重视并加强训练.

4 几点思考

4.1 重视数学阅读教学，提高学生的阅读能力

学生有早读课，一般读语文或英语，有的学校还设有晚读课，读政史地，因此，阅读早已成为文科学习的一种常见形式.数学需要阅读吗？2020年初，《中国高考评价体系》的发布和实施以来，高考命题方向发生了显著的变化，高考试卷逐步突出对学生关键能力的考查，而“阅读理解能力”是数学学科高考着重考查的关键能力(阅读理解、信息整理、语言表达、批判性思维)之一.同时，在信息社会，数学阅读理解也是学习和生活的一项基本技能.纵观近几年的高考数学试题，一方面题干的文字不断增多，篇幅逐渐增长；另一方面，更加突出问题情境、理性思维及对新知识的理解运用.例如，2022年全国数学新高考Ⅰ卷的第4题，问题虽然很简单，只是考查了台体的体积公式，但整个题目近150个字符，并以“南水北调、水库、海拔高度”等现实生活中的素材为背景，称得上是一个小型的“阅读理解”试题.

长期以来，高中数学教学实践主要以“解题”与“思考”为主，不太重视“阅读”与“表达”，导致学生在数学学习中阅读兴趣低、习惯差、阅读视野狭隘，缺乏耐心及自主性，阅读能力不容乐观[2].这不仅与数学本身的逻辑严密性、高度抽象性及语言的多样性(符合语言、文字语言、图形语言等)有关，还与缺乏正确的阅读指导有一定的关系.因此，教师应加强对学生数学阅读的指导，为学生提供丰富的阅读素材，营造良好的阅读氛围，继而提高学生的阅读兴趣.特别要通过加强对数学语言的教学，培养学生对数学语言的“互译”技能，形成“数学语感”，扫清阅读障碍，教师应适度介绍阅读理解的方法，逐步提高数学阅读理解的要求，并建议尝试在课程安排上开设数学阅读课，至少要将数学阅读纳入课堂教学环节之中，并加强阅读训练与评价.

4.2 发挥数学文化资源在数学课堂构建中的作用

《普通高中数学课程标准(2017年版)》(以下简称《课标》)明确指出，在实施教学时，应将数学文化融入教学活动中去，引导学生了解……提升学生的学科素养、应用意识和人文精神.近年来，各地数学高考试卷中也出现了不少关于“数学文化”的题目，这不仅是一个导向，也充分体现了数学文化在中学数学教学与学科育人方面具有不可或缺的应用价值.《课标》还指出，将数学文化融入数学教学，有利于激发学生的学习兴趣、开阔学生的知识视野，帮助学生理解数学、提升核心素养.数学文化的价值不仅在《课标》中得到肯定，同时在数学教育和数学共同体内也获得了越来越多的学者和一线教师的广泛认可.因此，教师要提升对数学文化的认识，增加数学文化的知识储备，掌握必要的方法，充分利用新教材的章首语、课题引入背景、习题、例题、阅读材料、数学写作、数学建模、信息技术应用等诸多环节，不断渗透数学文化，将数学文化深入课堂、融入生活，充分发挥数学文化资源在数学课堂构建中的作用，增强数学文化的渗透力和吸引力，进而实现立德树人的学科育人目标.

在此需要特别强调的是，数学文化除上述诸多元素外，还包括当前社会、科技等方面的热点问题，以此类素材为背景的考题，在新高考试卷中屡见不鲜.

4.3 在问题的解决中，培养学生的创新意识

数学问题的基本要素包括条件和结论.问题的解决一般从条件出发，在目标的牵引下，运用各种认知活动、技能方法等，经过一系列的思维操作，使问题得以解决的过程.常规试题的条件及结论具有明确性、指向性、目的性等特点，按照常规的思维方法基本可以形成解题思路，解题过程具有一定的规律性.而旨在考查学生创新能力的试题，其条件和结论在结构上不完整，指向也不明确，甚至有不相融的一面[3].例如，新高考中的结构不良试题、答案不唯一(开放型)试题、新知阅读题等.在教学中，教师要不断地探索此类问题的命题特征，特别是新知阅读题，要探索“新”在何处——是题目构建新颖、条件太宽泛还是结论太开放？要引导学生总结其中的异同点，引导学生在多种解法中，打开自己思维的“阀门”，给予学生大量的思维发散空间和问题解决的平台，只有这样，才能在问题解决的过程中逐步培养学生的创新意识，继而形成此类问题的解决路径.