对数的两个性质及其应用
——从一道教材习题的创新解法谈起
张志刚
(宁阳县复圣中学,山东 宁阳 271400)
1 问题的缘起
2019年人教A版普通高中教科书《数学(必修1)(下文简称教材)第141页有如下习题:
例1比较下列3个值的大小:log23,log34,log45.
本题比较底数互不相同的对数式的大小,具有一定的思维难度.如果要针对每一个底数分别计算出相应的对数,那么“简化运算”就是一句空话.能否把其他数为底的对数都转化为某个数为底的对数[1]?我们先回顾与教材配套的《教师教学用书》给出的解答:
即
log23>log34.
同理可得
log34>log45,
于是
log23 >log34>log45.
以上采用作差法来比较对数式的大小,首先利用对数的换底公式将对数式都转化成常用对数,再综合利用基本不等式等工具连续放缩,最终完成大小关系的判定.解答过程迂回辗转,较为烦琐.那么,有操作性更强的方法吗?

于是,我们类比猜想不等式log23>log2+1(3+1),即log23>log34是否成立呢?事实上,由“糖水不等式”得
同理可得
log34>log45,
故
log23>log34>log45.
例1顺利获解.推而广之,当b>a>1,m>0时,logab>loga+m(b+m)是否也成立?
2 问题的探究
性质1logab>loga+m(b+m)(其中b>a>1,m>0).
证明由b>a>1,m>0,得
lnb>lna>0,
且
由“糖水不等式”得
即
logab>loga+m(b+m).
此外,当b>a>1,m>0时,
logab>loga+m(b+m)>0.
由不等式的倒数性质,得
即
logba 我们知道,代数学的根源在于代数运算,即加、减、乘、除、乘方、开方等,我们也可以通过运算发现和提出问题,促进学生数学思维的发展.例如,将logab>loga+m(b+m)(其中b>a>1,m>0)中的加法运算改为乘法运算,不等式演化为logab>logam(bm),是否也成立呢? 性质2logab>logam(bm)(其中b>a>1,m>1). 证明由于b>a>1,m>1,因此lnb>lna>0,且lnm>0.由“糖水不等式”得 即 logab>logam(bm). 此外,当b>a>1,m>1时, logab>logam(bm)>0. 由不等式的倒数性质,得 即 logba 以上我们从“糖水不等式”中获取灵感,猜想并证明了对数的两个不等式性质,利用它们可实现对数底数的置换,为比较不同底数对数式的大小提供了别样的视角.其解题步骤是:应用上述性质将其中一个对数式放缩为与另一个对数式同底数的对数式,再利用对数函数的单调性和不等式的传递性解题.例如,欲比较对数式logab,logcd(其中a≠c)的大小,首先应用上述性质放缩得logab 显然,这个过程对学生领会转化与化归思想、培养发现和提出问题的能力大有裨益.在解题教学过程中,教师要引导学生认真剖析题设条件和结论,通过观察、比较、联想、实验、概括、推理、证明等思维活动,选择合理的解题路径,避免死记硬背、生搬硬套“结论”的盲目机械训练.其中,要仔细体会对数的换底公式和“糖水不等式”在解题中的作用.下面举例说明. 例2设a=log36,b=log510,c=log714,则 ( ) A.c>b>aB.b>c>a C.a>c>bD.a>b>c (2013年全国数学高考新课标卷Ⅱ理科试题第8题) 解法1(常规解法)由对数的运算性质和换底公式得 又因为函数y=log2x在(0,+∞)上单调递增,所以 log23 从而 a>b>c. 故选D. 解法2(创新解法)由“糖水不等式”得 即 a>b. =log714, 即 b>c, 从而 a>b>c. 故选D. 例3已知55<84,134<85.设a=log53,b=log85,c=log138,则 ( ) A.a C.b (2020年全国数学高考新课标卷Ⅲ理科试题第12题) 解法1(常规解法)易知a,b,c∈(0,1),由基本不等式得 从而 a 由b=log85,c=log138,得 8b=5, 13c=8, 即 85b=55, 134c=84. 又134<85,则 134b<85b, 从而 134b<85b=55<84=134c, 于是 4b<4c, 即 b 综上所述,a 解法2(创新解法)由“糖水不等式”得 即 a 下同解法1. 评注在判定a,b的大小关系时,解法1思路不易探寻,且需综合应用对数的换底公式、基本不等式、放缩法等.解法2利用“糖水不等式”实施放缩,指向明确,简单易行. 例4若a>b>c>1且ac ( ) A.logab>logbc>logca B.logcb>logba>logac C.logbc>logab>logca D.logba>logcb>logac 故选项A,C项不正确. 解法2(作差法)因为a>b>1,所以 logba>logbb=1, 由a>c>1,知 logac 从而 logba>logac. 且 b2>ac>1, 则 lnb2>ln(ac)=lna+lnc, 即 2lnb>lna+lnc, 于是 logcb-logba>0, 即 logcb>logba. 综上所述,logcb>logba>logac.故选B. 解法3(创新解法)因为a>b>c>1,且ac 即 logcb>logba>logac. 故选B. 评注解法1采用特殊值进行解答,看似轻松,然而本题限制条件较多,能否顺利列举出合理的特殊值面临较大挑战.解法2首先通过插入中间值1,先比较logba与logac的大小,然后采用作差法比较logcb与logba的大小,解答过程需要综合应用对数的换底公式等性质,并结合题设条件“ac 证得 logba>logac. 例5设a=log0.20.3,b=log20.3,则 ( ) A.a+b C.a+b<0 (2018年全国数学高考新课标卷Ⅲ理科试题第12题) 解法1(常规解法) 因为lg 2-1 即 a+b<0. 又a>0,b<0,从而ab<0,于是 =log0.30.2+log0.32=log0.30.4 =1, 因此 ab 故选B. 解法2(创新解法)由“糖水不等式”得 从而 a<-b, 即a+b<0.下同解法1. 数学解题是巩固基础知识、落实基本技能、感悟思想方法、培育核心素养、提升思维敏锐度的系统活动,是掌握数学、学会“数学地思维”的关键途径.追求解题过程的简单,追求思维过程的经济,是解题研究的一项基本任务,也是数学工作者的一个共同性格.在解题坐标系中,表现为解题折线的简短或思维链的优化[2].在数学探究中要培养学生善于自主发现、提出问题,启发、引导学生对不同的对象通过类比推理提出问题、做出猜想是培养学生问题意识比较有效的途径[3].前文正是从一道教材习题开始,结合已有的学习经验,通过观察、联想等活动,发现了对数的两个不等性质,并用它们解决了一些比较对数式大小的问题.当然,此类问题有待深化研究.例如,本文仅讨论了“b>a>1”的情形,如果“0
3 性质的应用

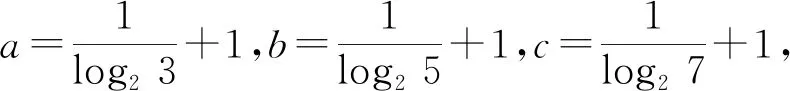






4 结束语

