立足解题教学 精准渗透模型思想
——以一道模考综合题的教学策略为例
王 龙, 柳 雪
(1.青浦区实验中学东校,上海 201700;2.青浦区实验中学西校,上海 201700)
数学模型是指使用数学符号、公式、程序、图形等实际问题的本质属性进行抽象而简洁的刻画来解释某些客观现象、预测发展规律,或找出化解实际问题的最优策略[1].构建数学模型解题应先具备模型观念,从具体情景中抽象出数学问题,感知数学建模过程并解决问题,进而形成模型思想.然而,学生在面对综合题时往往难于从中感知组成几何图形的各要素,不能与基本图形建立关联,不会通过几何直观把握问题的本质,从而导致思维路径不清、难以取得突破.课堂上由于教学内容多、时间短,教师对综合题缺乏深入研究、教学不精准,教学过程就题讲题,重思路、轻梳理,重过程、轻归纳,导致教学效果不理想、学生收获不大.为了改变这个现状,笔者在初三模拟测试后针对压轴题的教学做了些许尝试,与读者分享.
1 问题呈现
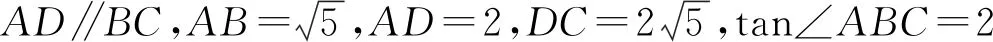
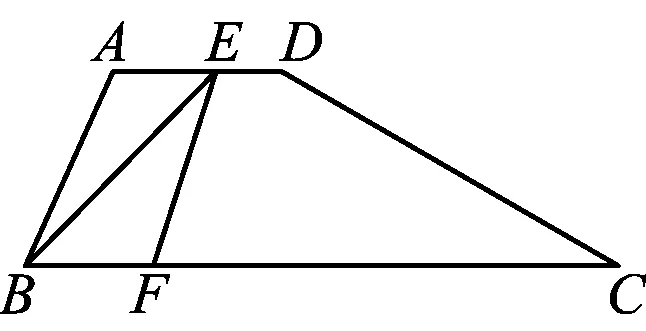
图1
1)求线段BC的长;
2)当FB=FE时,求线段BF的长;
3)当点E在线段AD的延长线上时,设DE=x,BF=y,求y关于x的函数解析式,并写出x的取值范围.
(2021年度上海市青浦区初三数学一模试题第25题)
2 策略分析
建模思想的形成要从培养模型意识开始.前两个小题相对比较简单,与已经具备的知识建立关联解决问题,培养学生的建模意识,感知模型观念的必要性、根植模型观念.在探究第3)小题的过程中,用不同的方法建模解决难题,提升学生的建模能力,然后通过反思小结、校正补偿训练形成学生的建模思想.
3 实施过程
3.1 寻找关联,感悟套用模型
第1)小题已知梯形的三边和一角,求梯形的第四边,类似于三角形中已知两边和一角求第三边的问题,常规方法是添线构造直角三角形解决.找到与已知模型的关联后,尝试添辅助线解决问题.思考后发现:可以通过下面3种添线方法(如图2~4),构造出一个特殊的四边形和两个直角三角形解决问题,从条件tan∠ABC=2入手解直角三角形.

图2 图3 图4
设计意图套用已学过的解三角形的模型解决四边形问题,感悟模型的重要性,强化了套用模型解题的意识.
3.2 抽象问题,根植模型观念
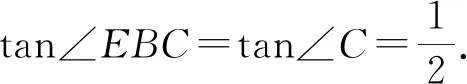
如图5,过点E作BC的垂线EM,由FB=FE得
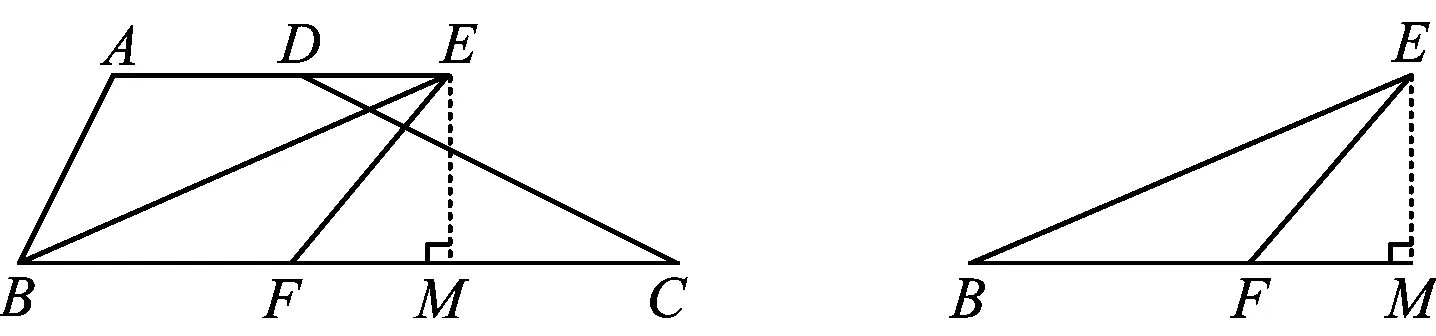
图5 图6
∠EBC=∠BEF=∠C,
可知
在Rt△EMF中,
(4-BF)2+22=BF2,

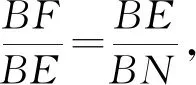

图7 图8
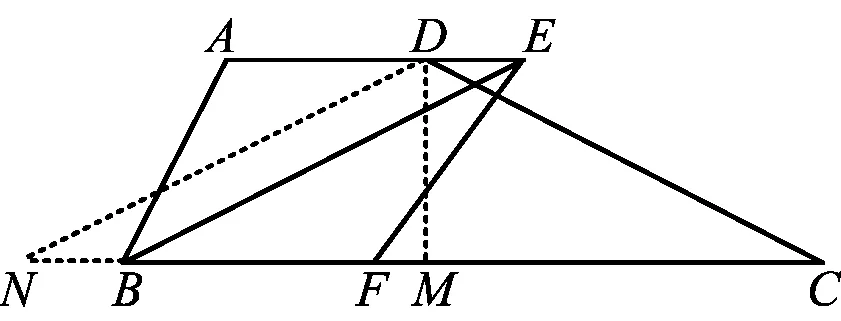
图9
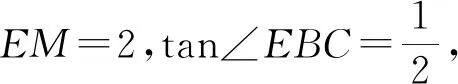
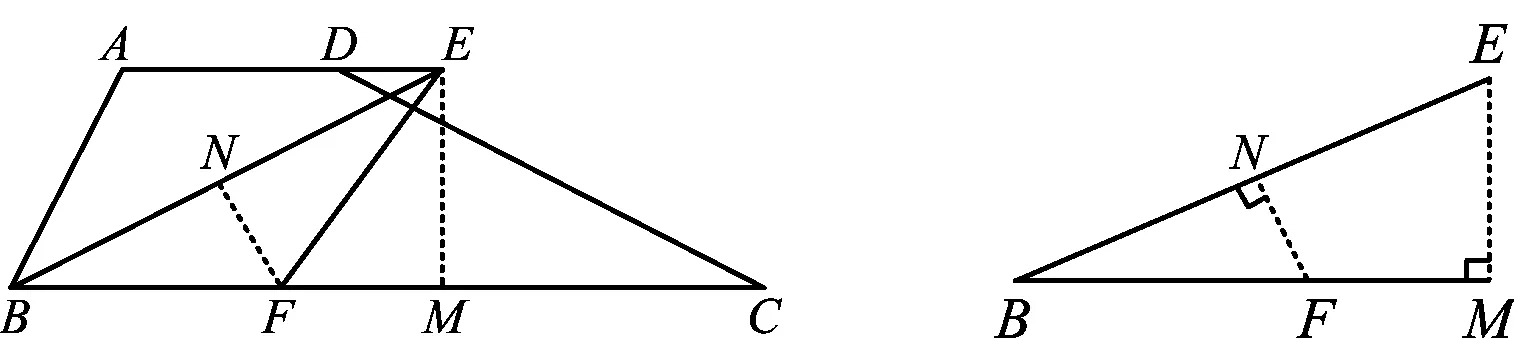
图10 图11
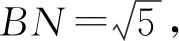
设计意图解决第2)小题的方法比较灵活,以不同的方式添加辅助线构造基本图形(如图6,8,11),以抽象的基本图形作为模型解题,阐释了模型应用的广泛性,根植模型观念.
3.3 突破难题,提升建模能力
数学模型是对数学内容的高度抽象与概括,是最本质且最简练的表达.破解难题应找到最本质的模型,解决第3)小题的要点是恰当使用条件∠BEF=∠DCB.主要的建模方式有以下几种:
3.3.1 基于通性通法建模
通性通法是具有代表性的解题方法,是解题教学中应该凸显的重点内容.建立模型解决问题首先应该考虑普适性的方法,具有代表性的模型最具备研究学习的价值.如图7添辅助线,构造一个如图8的“斜A型图”结合勾股定理解决:由△BEF∽△BNE,得
BE2=BF·BN=y(x+7).
在Rt△BEM中,由勾股定理得
BE2=x2+6x+13,
即
x2+6x+13=y(x+7).
整理后得
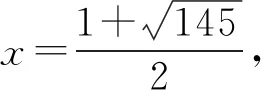
设计意图结合相似比和勾股定理建立数学模型是解决综合题的常用方法,需要师生多思多悟,掌握了这种模型对解决综合题大有裨益.
3.3.2 在原图中寻找模型
模型的构造不一定都需要添加辅助线,有的时候模型就藏在图形之中,需要我们用数学的眼光去观察和发现.如图12,记BE与CD相交于点K.由△BKC∽△BFE,得

图12
由AE∥BC可得
即
因此

代入相似比,可得
化简得
由一组相似三角形与“X型图”相结合的模型即可解决问题.同理,在原图中由△EDK∽△BEF结合AE∥BC得到比例,同样也可得到y与x之间的函数关系式.
设计意图结合相似比和基本图形建立数学模型也是破解综合题的常用手段.通过几何直观在原图中寻找、剥离出基本图形与相似找关联并建模,在探究思考过程中提升建模能力.
3.3.3 多向思维建立模型
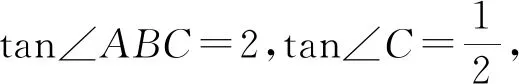
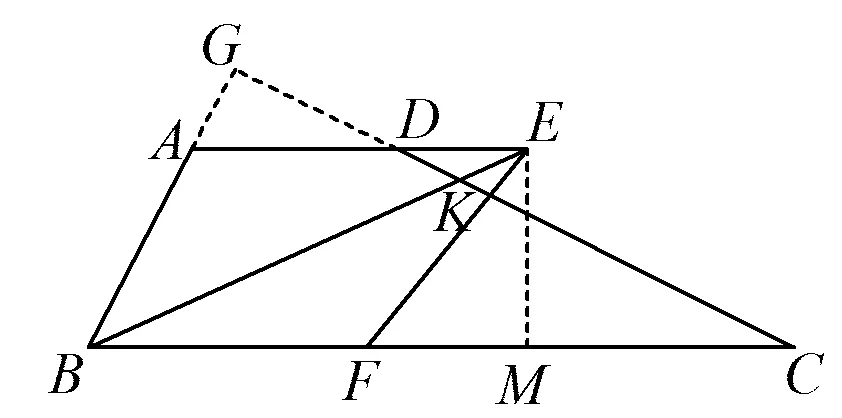
图13
从而
于是
由∠BKG=∠EFM,得
cot∠BKG=cot∠EFM,
即
代入得
化简可得
设计意图多向思维发现了∠G为直角,从而找到一种新的方法建立模型解题.虽然过程有些复杂,但有助于透彻理解不同的建模方法,是锻炼建模思维能力的一种有效途径.
3.3.4 拓展思路建立模型
有时候用高中的知识解决初中的问题会使得难题简单易懂,例如两角的和差公式在初中阶段经常运用.笔者认为有必要拓展,如图5添加辅助线,由于角度之间存在关系∠EFC=∠EBC+∠C,而这3个角的正切也容易表示出来,即
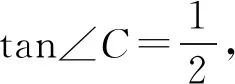
化简得
设计意图由公式所确定的模型简单且容易掌握,在教学中具备较高的学习价值.
3.4 总结提升,渗透建模思想
以学生为主体的精准教学中,教师的主导作用不仅是要把学生往正确的解题思路上带,更应该帮助并带领学生树立模型意识、促进学生自主思考、建立并运用模型解决问题.例如第1)小题要与已知模型找关联;第2)小题要应用好条件FB=FE,抽象建模;第3)小题的关键是要用好条件∠BEF=∠DCB,由相似结合其他要素建模,在套用、尝试、多角度的建模过程中提升建模能力、形成模型思想.
4 矫正补偿,巩固模型
精准教学不仅要求课前精心设计学案,课中促进高效学习,课后也要精准训练.精准设计反馈练习要做到针对性强,量少且精.首先,设计的作业必须与解题教学有关,能用到课堂上学到的思想与方法,起到夯实基础、巩固旧知的效果.其次,设计的作业思维容量应有所提升,在最近发展区寻找学生思维能力的增长点,在原有知识的基础上通过训练达到发展学生思维的效果.最后,设计的作业能起到优化学生知识结构、构建知识系统、提升学生数学素养的效果.结合以上几点,笔者对课后作业做了如下设计:
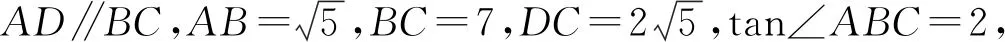
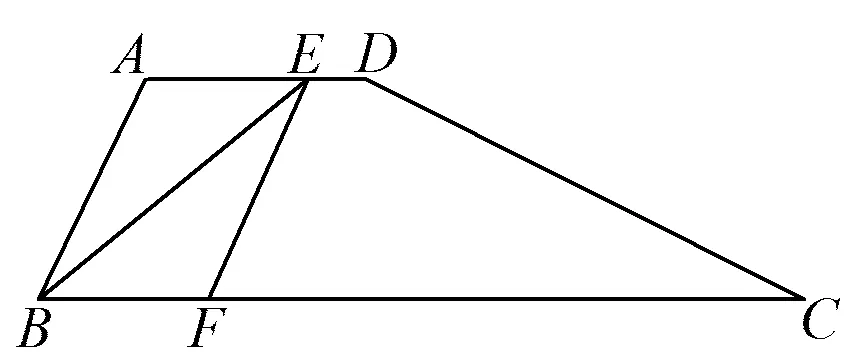
图14
1)求线段AD的长;
2)当四边形ABFE是平行四边形时,求线段DE的长;
3)设DE=x,BF=y,求y关于x的函数解析式,并写出x的取值范围.
设计说明本题与例1的思想方法基本一致,每一个小题的建模方式也大致相同,解题过程不再赘述.利用此题能够夯实基础,巩固课堂所学的数学模型.
变式2如图15,在梯形ABCD中,AB∥CD,∠B=90°,AD=15,AB=16,BC=12,点E是边AB上的动点,点F是射线CD上一点,射线ED和射线AF交于点G,且∠AGE=∠DAB.
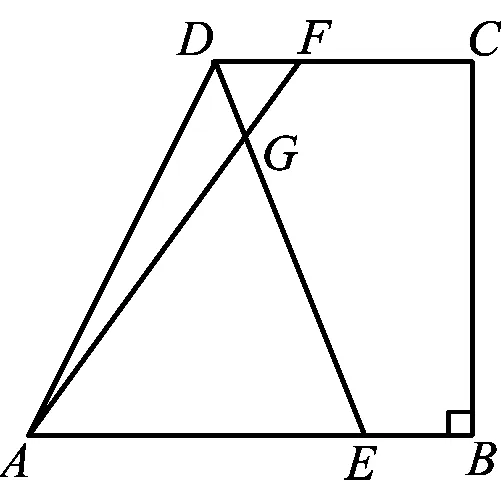
图15
1)求线段CD的长;
2)如果△AEG是以EG为腰的等腰三角形,求线段AE的长;
3)如果点F在边CD上(不与点C,D重合),设AE=x,DF=y,求y关于x的函数解析式,并写出x的取值范围.
(2016年上海市数学中考试题第25题)

经过对例1的深入学习后,本题处在学生知识的最近发展区,努力解决本题可以促进学生形成建模思维.同时,例1和两个变式都是梯形背景下的综合题,涉及基本图形、相似三角形等知识.为学生以后解决梯形背景下的几何问题提供了思考方向,完善了学生的数学知识体系,精准提升了学生的数学素养.
数学建模不仅是学生数学核心素养的重要组成部分,也是解决数学问题的重要思想[2].在初中数学课堂教学中培养学生的建模思维,有利于提升学生发现问题和解决问题的能力,促进学生数学思维能力的发展.然而,学生的建模思维不是一蹴而就的,需要教师对学生进行精心细致的培养,要把数学建模思想贯穿于教学始终,在课堂有限的时间内精准教学,让学生认识到数学建模在生活中的重要价值,激发学生学习的积极性和主动性[3];培养学生建模实践的能力,在生活中与实际问题相结合,真正做到学以致用,最终形成数学建模思想,实现提升核心素养的目标.

