对一道几何最值问题的多角度剖析
陈 刊, 吴 凯
(1.开元中学,浙江 杭州 310000;2.菱湖中学,浙江 湖州 313018)
《义务教育数学课程标准(2022年版)》(以下简称《新课标》)在课程内容“图形与几何”中提出从演绎证明、运动变化、量化分析这3个方面研究图形的基本性质与相互关系[1].中学数学在知识内容、思想方法、应用层次上都存在差异,导致一个几何问题从思路分析到解题路径截然不同.但观察问题、思考问题和解决问题的模式是相通的,培养和发展核心素养的目标也是一致的.同时解题教学能有效帮助学生完善知识体系,提升思维品质.本文通过对一道几何最值问题的多角度解题剖析,帮助学生更好地理解数学内容的有机融合.
近日,笔者有幸聆听了杭州某地区一节高二期末复习公开课,课堂上的一道几何最值问题,引起了笔者的关注.
1 原题再现
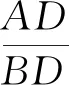
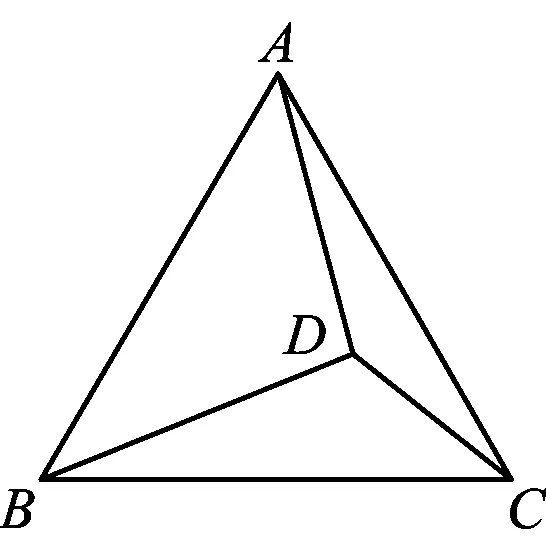
图1
2 几何图形特征分析
例1是以等边三角形为背景、角度为定值的条件下,求两线段之比的最小值,主要考查学生的推理能力和运算能力.从角的特殊性出发寻找边的特殊性,具有极强的平面几何题目的典型性.初中学生完全有能力运用平面几何的方法求解.
从已知条件分析,关键条件∠BDC=120°结合等边△ABC,通过∠DCB+∠DBC=∠DBC+∠ABD=60°可以转化成∠DCB=∠ABD.中考题通常只讨论一条线段的长度取值,因此从结论分析,求两条不确定线段之比确实难度不小.
3 解题剖析
角度1构造辅助圆及其性质.
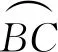
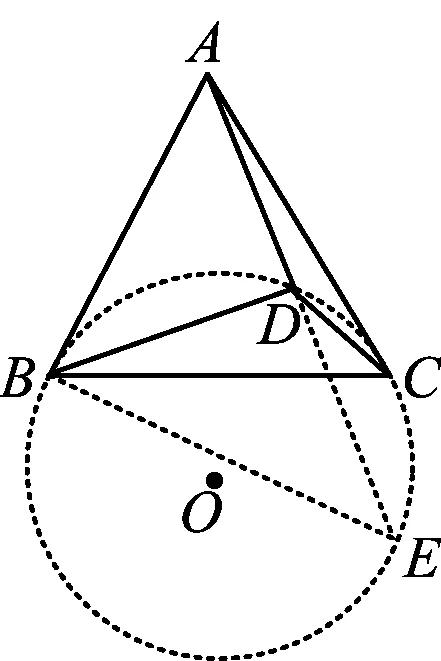
图2
由∠DCB=∠AEB,且∠DCB=∠ABD,得
∠ABD=∠AEB,
又
∠DAB=∠BAE,
则
△ABD∽△AEB,
可得
故
评注《新课标》提到“理解图形变化中的不变量”.本题AD与BD的长度变化由点D位置的不确定引起,只要抓住点D与边BC两端构成张角不变,就能确定出点D的运动轨迹——圆弧.这样的思考过程正符合了空间观念的内涵之一“表达关键物体的空间位置和相互之间的关系”.不断转化条件,既训练学生的推理能力,又逐步发展学生的空间观念.
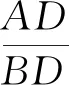
角度2联系费马点问题的图形旋转.
费马点是到三角形的3个顶点的距离之和最小的点.
如何找费马点?如图3,P为△ABC所在平面上的一点,将△BPC绕点B旋转60°到△BP′C′的位置,联结PP′,则△BPP′为正三角形,从而
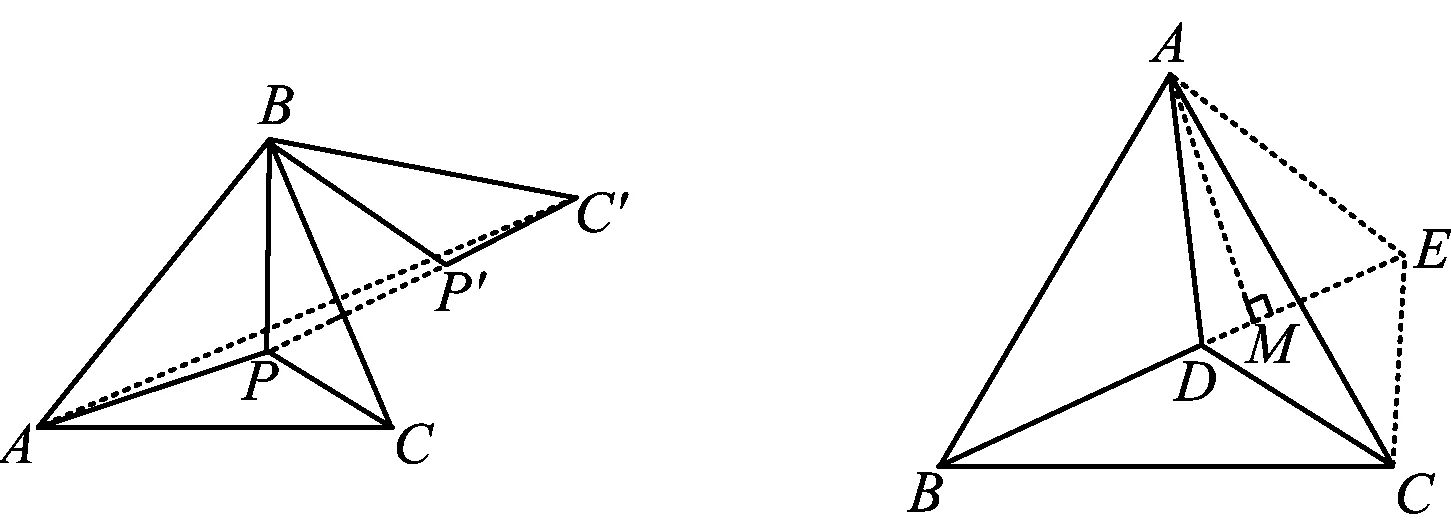
图3 图4
PA+PB+PC=PA+PP′+P′C≥AC′.
当点A,P,P′,C′共线时,PA+PB+PC为最小.此时,点P为△ABC的费马点.
评注将△BPC绕点B旋转60°,是费马点问题证明中的点睛之笔.通过旋转变换,将线段PC转化到P′C′;通过等边三角形,将线段PB转化到PP′.两次转化打开了3条线段求和的新局面,基于这样的思路,不妨旋转部分图形.
解法2如图4,将△CBD绕点C顺时针旋转60°到△CAE,联结DE,则
BD=AE, ∠AEC=∠BDC=120°.
因为CD=CE,∠DCE=60°,可得△CDE为等边三角形,其中∠CED=60°,所以
∠AED=∠AEC-∠CED=60°.
作AM⊥DE于点M,则
评注旋转的本质在于构造全等三角形,利用对应边相等将AD,AE(BD转化)集中到△AED上,在△AED中∠AED是已知角.从三角形边角关系分析,已知一角,求对边与邻边的比值范围,运用三角函数相关知识最佳.
通过旋转变换,关键条件∠BDC=120°化身成了等边△DCE,将费马点问题的证明过程作为解题思路的启发,有助于打破原有图形条件的束缚,在新的关联下找新的突破.用学过的知识和方法解决简单问题,有利于发展核心素养中的应用意识.
角度3巧妙联想三角形正弦定理.
如图5,前文分析将关键条件∠BDC=120°转化成∠1=∠2,不难发现:所求线段AD与BD分别是△ADB和△BDC中∠1和∠2所对的边.由这样的边角关系容易想到正弦定理.
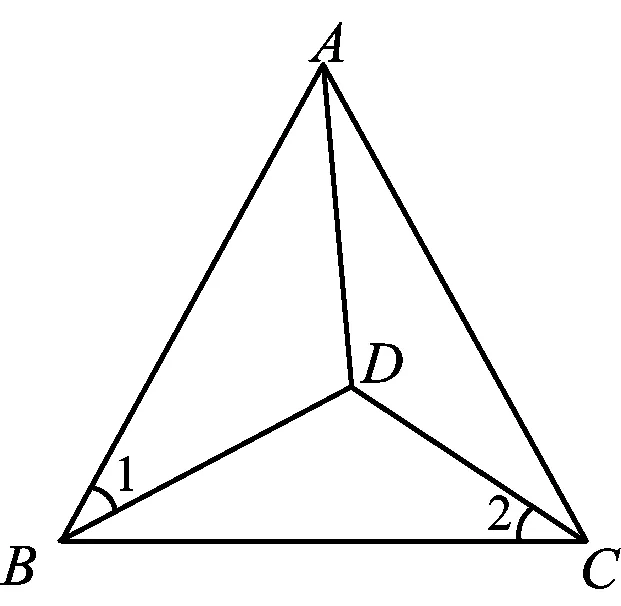
图5
解法3由题意可知,在等边△ABC中,∠BDC=120°,可得∠1=∠2,且AB=BC,则由正弦定理可得
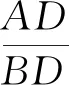
角度4解析几何思想的运用.
《新课标》提到初中阶段几何与图形领域还包括了“图形与坐标”这个主题.初中生受限于解析几何知识储备不足,尚不能将题目量化分析,但高中课堂中解析法可“大放光芒”.
通过建立平面直角坐标系,利用待定系数法求出点D的轨迹方程.确定轨迹后,可利用两点间的距离公式表示线段的比,通过对二元二次分式的处理,转化为斜率的最值问题,再利用相切关系求出最值.
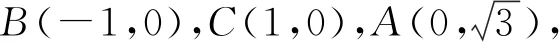
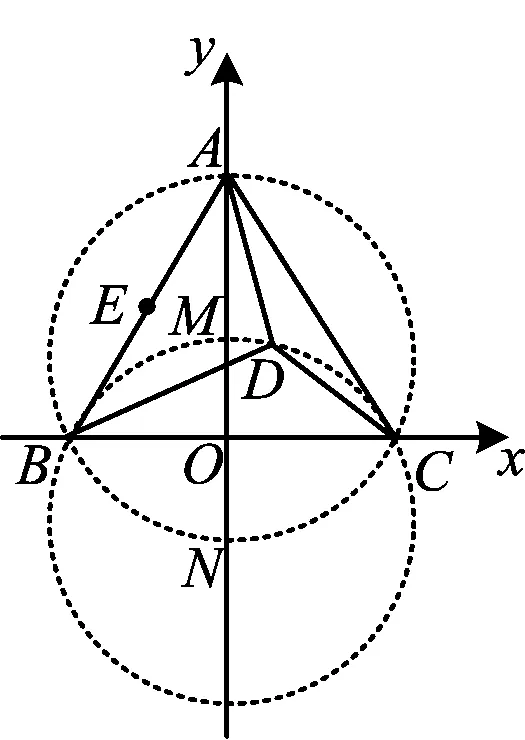
图6
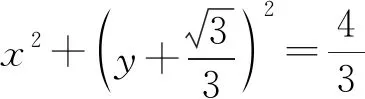
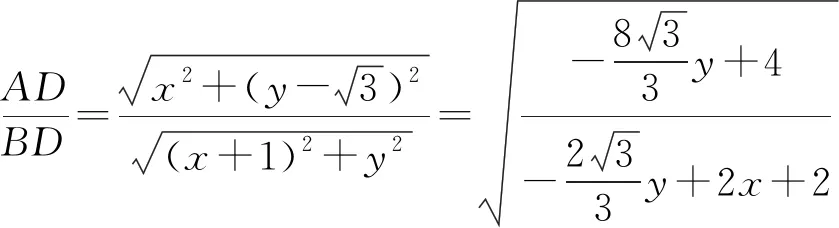
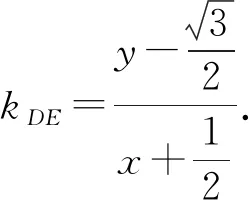
圆心N到直线DE的距离为
化简得
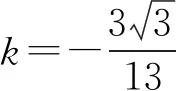
评注该解法充分运用了解析几何的思想精髓,从坐标到轨迹,从线段比到斜率,过程如行云流水,环环相扣,知识点清晰且明确,对学生的计算能力提出了极高的要求.解析法体现了“坐标化”的特点,更加适合方程化运算,无形中也弱化了解决几何问题本该具备的逻辑推理能力.但经历从几何特征思维跃迁至代数运算思维,不禁感叹数学运算的神奇魅力.
4 解法反思
4.1 几何解题的核心思想——转化
核心素养要求以数学的眼光观察现实世界,而几何解题的眼光就是戴着转化的“有色眼镜”观察、分析几何的图形特征.罗增儒教授提出:“寻找解题思路的过程就是寻找条件知识与结论知识之间的逻辑联系或转化轨迹的过程.”[2]解法1~3均突出了几何图形的转化.如∠BDC=120°可以结合等边三角形转化成两个角相等,或利用它的邻补角60°为构造等边三角形搭好平台等.
学生面对几何问题时难以一下子找到方向,主要在于缺乏转化的眼光.教师在教学中可多些总结,如线段、角的转化都有哪些常见的几何基本图形等.譬如利用轴对称性,把一侧的边角关系转化到另一侧;利用两个三角形之间的特殊关系(构造全等或相似三角形),对应的边角之间的转化.
4.2 数形结合研究几何的利器——解析几何
平面直角坐标系是数轴的发展,是沟通几何图形与代数运算的重要纽带.解法4利用坐标系充分量化图形,用纯代数的方法表达图形的变化.初中生虽然知识储备上不及高中学生,但尝试用代数方法研究几何图形特征的做法值得提倡.在感悟数形结合意义的同时,充分发展学生的几何直观、推理能力和运算能力.
4.3 几何解题的核心美感——简洁
核心素养要求以数学的语言表达现实世界,几何的语言是无懈可击的简洁语言.解法1和解法4中隐藏圆,挖掘定角背后的运动轨迹;解法2与大名鼎鼎的费马点问题产生共鸣,旋转构造一对全等三角形和等边三角形,前者是两个三角形的特殊关联,后者是特殊的三角形;在解法3中,两个三角形各自一边对一角,运用正弦定理巧妙地推出新的一边对一角,此法无须新图形的构造,解题过程亦少,最为简洁.
4.4 几何解题直觉的积累——实践
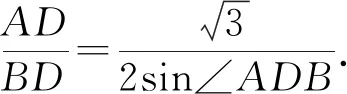
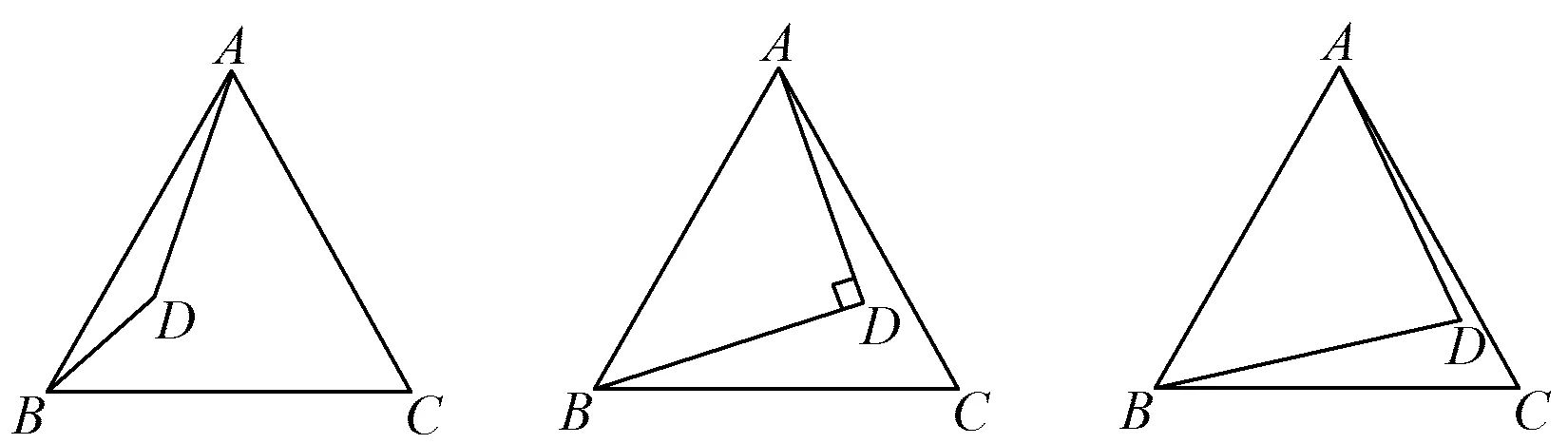
图7
5 拓展与变式
5.1 条件一般化
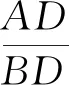
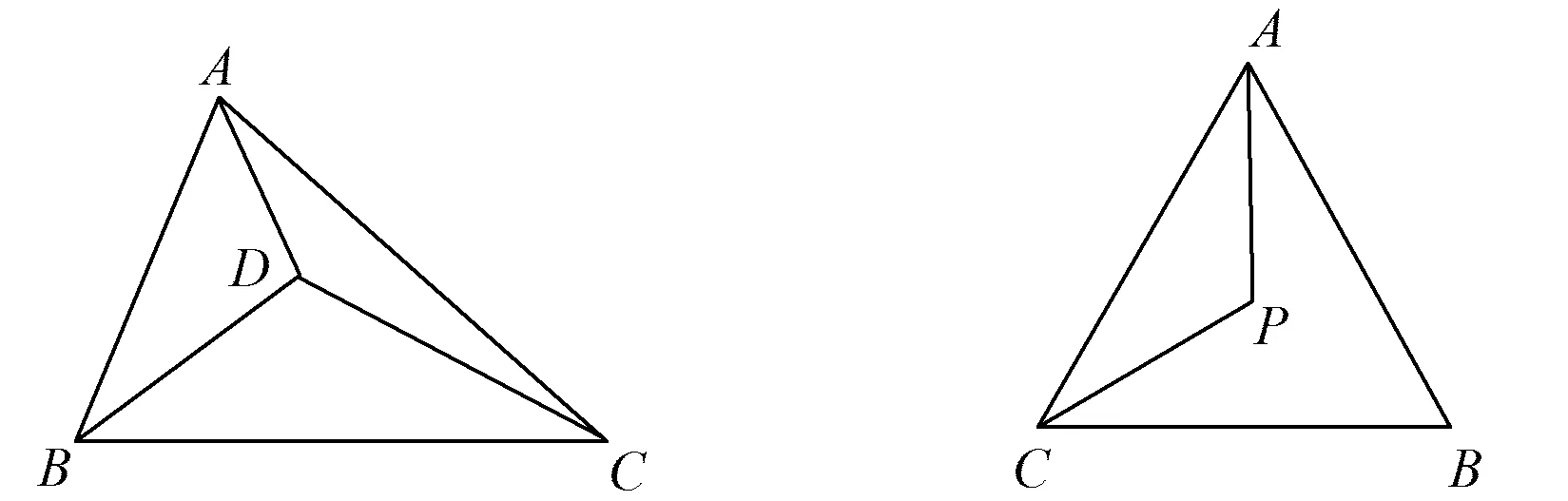
图8 图9
5.2 各类变式
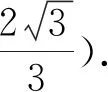
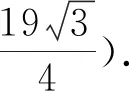
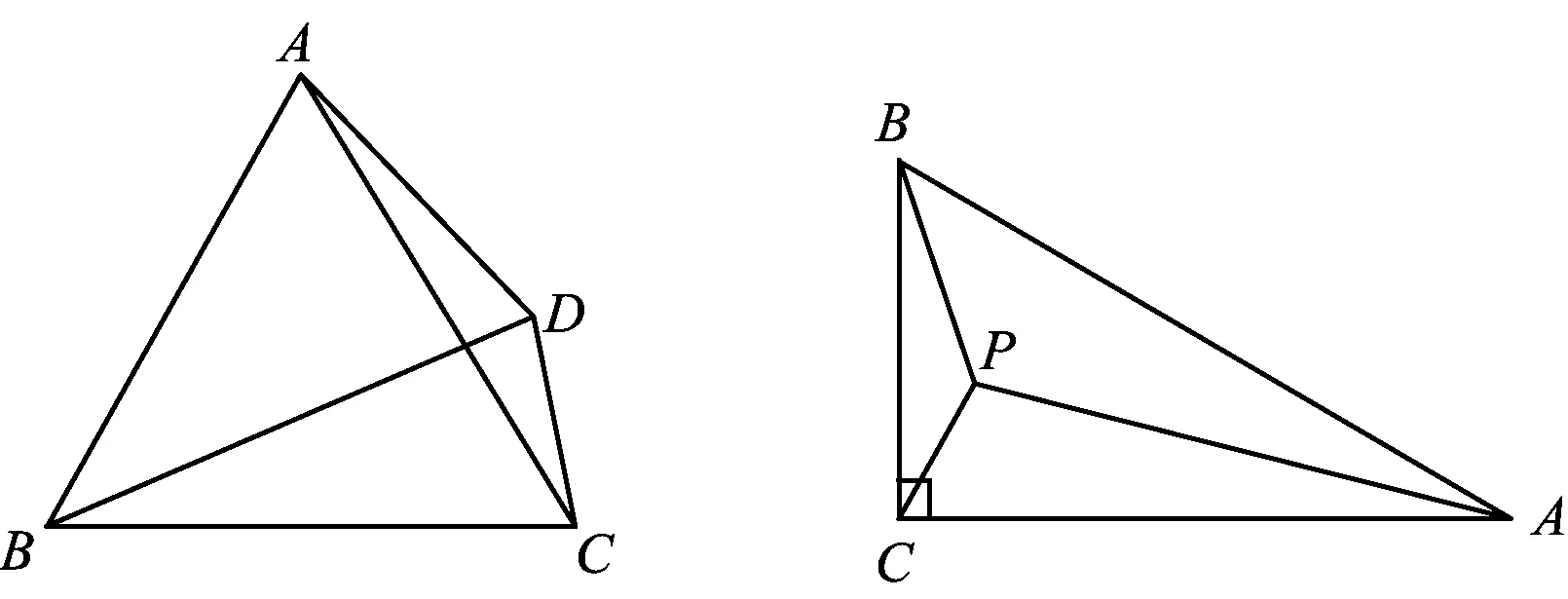
图10 图11
6 教学启示
数学知识的积累往往是从无到有、从简单到复杂、从“杂乱”走向“有序”的渐进过程.解决几何问题,初中阶段倾向于平面几何证明,而到了高中阶段,则更倾向于用解析几何方法,这源自数学发展史上笛卡尔平面直角坐标系的发现及其被世界广泛认可、接受和推广运用的发展过程,这是自然的、客观的、有历史可考证的,符合人类思维进化的正常发展模式.中学数学的主要思想方法并没有明确的阶段划分,教学也不应存在思维壁垒.如图12,学习数学的过程本质从未发生改变.
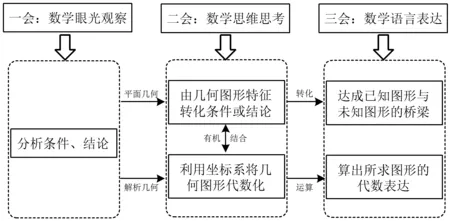
图12
正如章建跃博士所说:“在用代数语言转化几何问题前,一定要注意用几何的眼光分析面临的问题.”[3]倘若教师在几何解题教学中以数学学科核心素养为依托,有机融合数学知识,在数学的整体性、逻辑的连贯性、方法的普适性上动足脑筋,做好学生数形结合能力的培养,不仅有助于拓宽学生的视野、优化解题思路、合理减少运算量、提高解题效率,更能点燃学生学习数学的热情,提升课堂的活力,中学数学的课堂会更加精彩纷呈.

