2022年全国数学高考卷立体几何试题分析及教学思考

逯彦周， 项丽红

(永登县第六中学，甘肃 永登 730300)

立体几何是研究现实世界中物体形状、大小与位置关系的数学分支，在解决实际问题中有着广泛的应用.立体几何章节是学生自然语言、符号语言、图形语言转换与学习的绝佳载体，承载着提升直观想象、逻辑推理、数学运算、数学抽象素养的数学使命.本文对2022年全国数学高考试卷中的立体几何试题进行统计分析，并对教学提出一些建议.

1 2022年“立体几何”高考试题统计

2022年数学高考试卷共9套，其中全国卷6套(分别为全国甲、乙卷文、理各1套，新高考Ⅰ、Ⅱ卷各1套，不分文理)，地方卷3套(分别为北京卷、天津卷、浙江卷各1套，不分文理，上海由于延迟高考，不做统计)，均考查了立体几何相关知识，共计28题.现将9套试卷中的立体几何试题按照题型、分值、考查内容、难度进行统计，结果如表1所示.

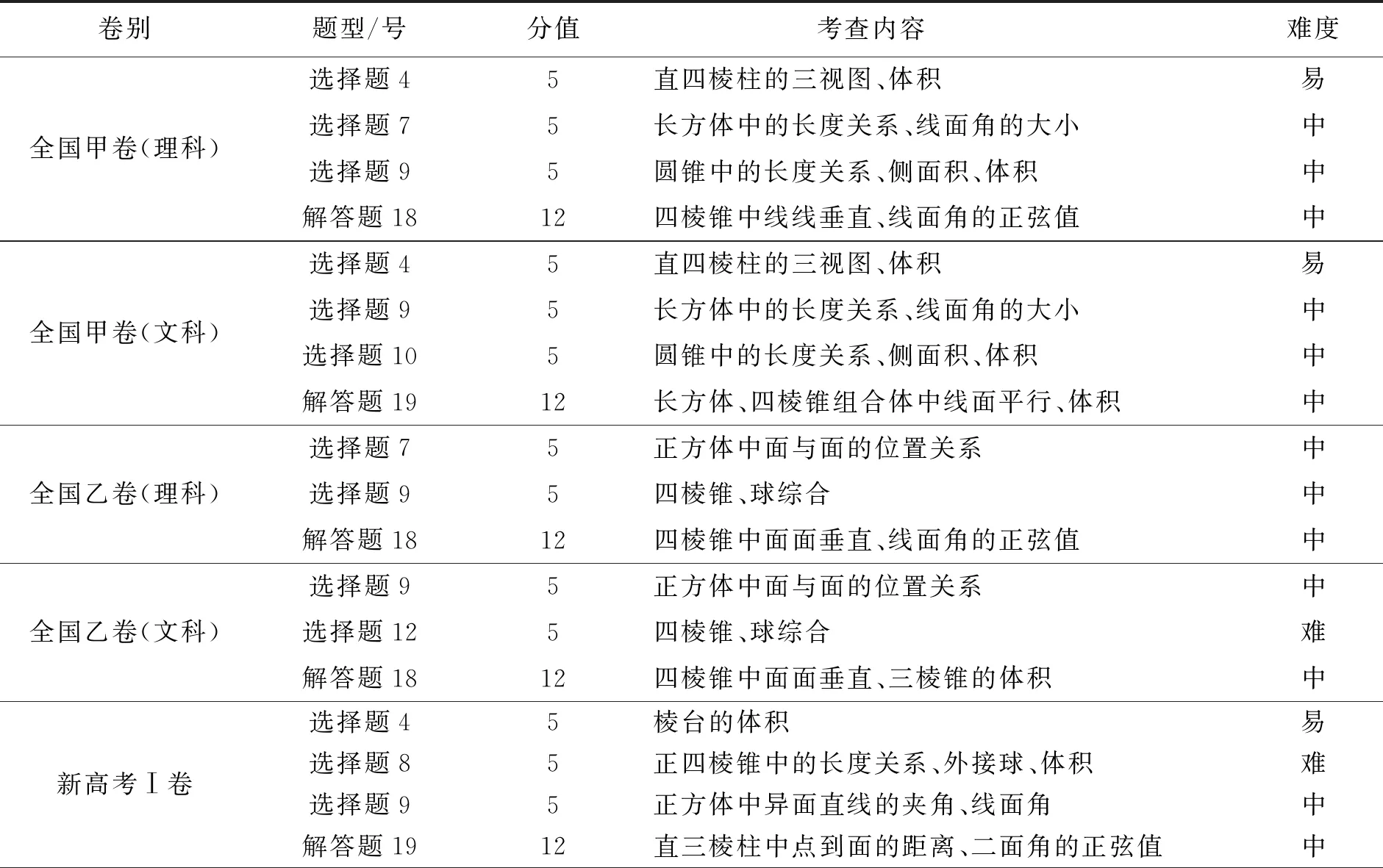
表1 2022年全国数学高考立体几何试题统计

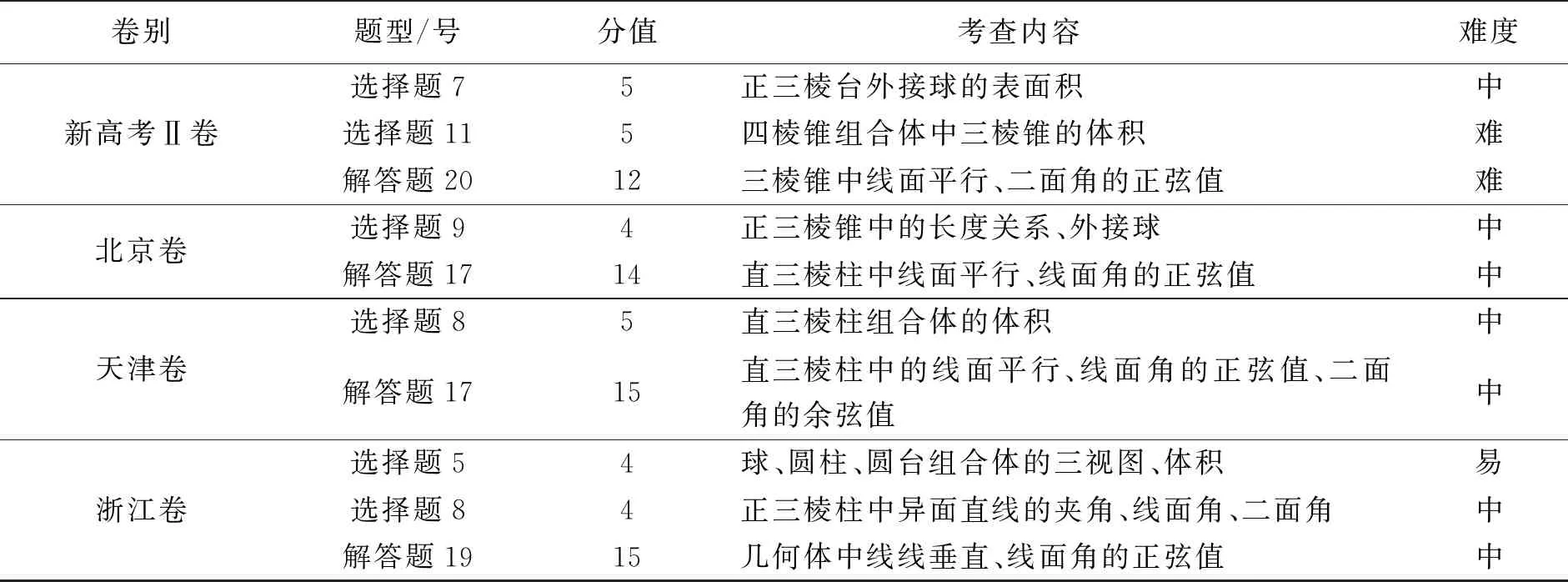
续表1

由表1知，从题型、分值看，9套试卷中立体几何试题均为选择与解答题，其中选择题19道、解答题9道.全国甲卷(文、理卷选择同题，解答不同题)与新高考Ⅰ卷均有3道选择题和1道解答题，共27分，占试卷总分的18%；全国乙卷(文、理卷选择同题，解答题第1)小题相同、第2)小题不同)、新高考Ⅱ卷及浙江卷均有2道选择题和1道解答题，其中全国乙卷(文、理)、新高考Ⅱ卷立体几何试题总分22分，占试卷总分的14.7%，浙江卷立体几何试题总分23分，占试卷总分的15.3%；北京卷与天津卷均有1道选择题和1道解答题，其中北京卷立体几何试题总分18分，占试卷总分的12%，天津卷立体几何试题总分20分，占试卷总分的13.3%.

从考查内容看，9套试卷中立体几何试题选择题的考点重点集中在棱锥、圆锥、棱台、球的体积和表面积，以及长方体(正方体)中的线面关系、长度、距离度量.解答题第1)小题考点重点集中于几何体中线线、线面关系的证明，第2)小题文科考点集中于几何体体积计算，理科及不分科考卷考点均为计算线面角、面面角的正(余)弦值.从难易程度看，9套试卷中立体几何试题以中等难度为主.

2 2022年“立体几何”高考试题特点分析

1)立体几何选择题涉及几何体形状规则，考点常规，题目经典中有创新.

19道立体几何选择题涉及几何体形状规则，其中载体为长方体、棱台的试题均为2道，载体为正方体的试题3道，载体为直棱柱试题4道，6道试题载体为棱锥，2道试题载体为圆锥，3道试题与球相关，与圆柱、圆台相关的试题均为1道.

19道立体几何选择题中12道题的落脚点(即答案涉及考点，下同)考查几何体的体积、表面积、侧面积，其中考查体积的有11道，占绝大多数，考查棱台、圆台体积各1道，需引起重视.19道立体几何选择题中7道题的落脚点考查几何体中线线、线面、面面位置关系及长度、夹角的度量，其中考查长度度量的有3道，考查位置关系的有2道，考查夹角度量的有4道.立体几何选择题题目经典，也有融合其他知识的创新，如全国新高考Ⅰ卷第8题、北京卷第9题.

( )

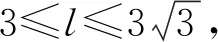
(2022年全国数学新高考Ⅰ卷第8题)

分析本题主要考查正四棱锥的外接球体积.由题意可求得正四棱锥体积是关于侧棱长l的4次函数，求最值用导数，知识融合程度高，难度大，重点考查学生的直观想象、逻辑推理、数学运算素养.设正四棱锥的高为h，由球的截面性质列方程求出正四棱锥的底面边长与高的关系，由此确定正四棱锥体积的取值范围.

解因为球的体积为36π，所以球的半径R=3.设正四棱锥的底面边长为2a，高为h，则

l2=2a2+h2， 32=2a2+(3-h)2，

从而

6h=l2， 2a2=l2-h2，

于是正四棱锥的体积

故

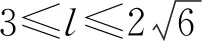
例2已知正三棱锥P-ABC的6条棱长均为6，S是△ABC及其内部的点构成的集合．设集合T={Q∈S|PQ≤5}，则T表示的区域面积为

( )

(2022年北京市数学高考试题第9题)

分析本题以正三棱锥为载体，融合集合知识，重点考查学生的数学抽象、直观想象、逻辑推理、数学运算素养，难度中等.求出以P为球心、5为半径的球与底面ABC的截面圆的半径后可求出区域的面积.

解如图1，设顶点P在底面上的投影为O，联结BO，则O为△ABC的中心，且

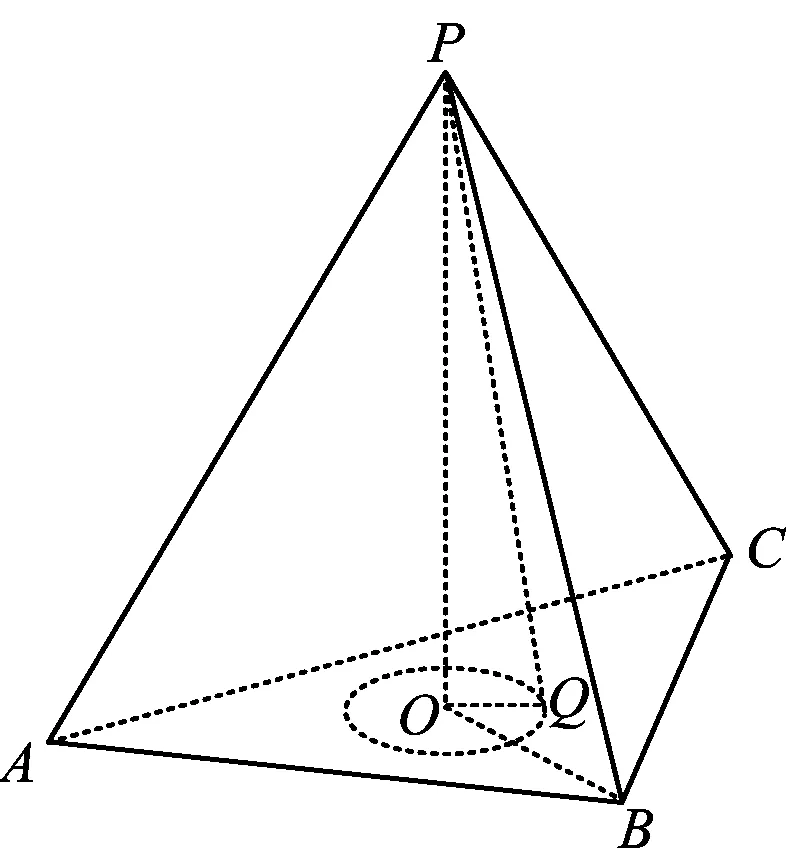
图1

当PQ=5时，OQ=1，于是点S的轨迹为以O为圆心、1为半径的圆.而△ABC内切圆的圆心为O，半径为

因此点S的轨迹圆在△ABC内部，其面积为π.故选B.

2)立体几何解答题逻辑证明步骤错综复杂，建系及坐标书写不易加大夹角度量难度.

9道立体几何解答题的第1)小题中有4道考查线面平行，2道考查线面垂直，2道考查线线垂直，1道考查点到面的距离，但均不能由题中条件直通答案，需要多步演绎推理才能得出结论.除去文科卷2道解答题，7道立体几何解答题中有3道题的第2)小题需要推理论证和计算才能找到三垂直建立空间直角坐标系，且坐标书写也需要经过一定的推理分析，因此大大增加了题目的难度.

例3如图2，在四面体ABCD中，AD⊥CD,AD=CD，∠ADB=∠BDC,E为AC的中点．

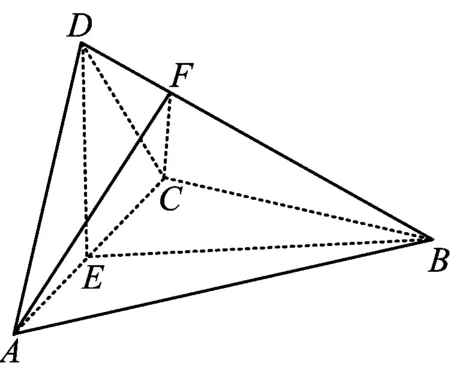
图2

1)证明：平面BED⊥平面ACD；

2)设AB=BD=2，∠ACB=60°,点F在BD上，当△AFC的面积最小时，求CF与平面ABD所成角的正弦值．

(2022年全国数学高考乙卷第18题)

分析本题以四面体为载体，第1)小题证明面面垂直，通过线面垂直证明面面垂直，从而需要证明线线垂直，用到了等腰三角形中线性质、三角形全等性质等.第2)小题在第1)小题的基础上需要证明BE⊥DE才能建系，建系后点F坐标的书写需要三角形相似的知识，需要证明、建系、计算，难度较大.

1)证明因为AD=CD，E为AC的中点，所以AC⊥DE.在△ABD和△CBD中，因为AD=CD,∠ADB=∠BDC，DB=DB，所以△ABD≌△CBD，从而AB=CB.由点E为AC的中点知AC⊥BE，又DE,BE⊂平面BED，DE∩BE=E，于是AC⊥平面BED.因为AC⊂平面ACD，所以平面BED⊥平面ACD.

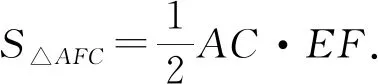
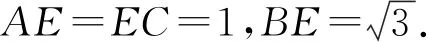
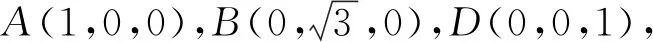
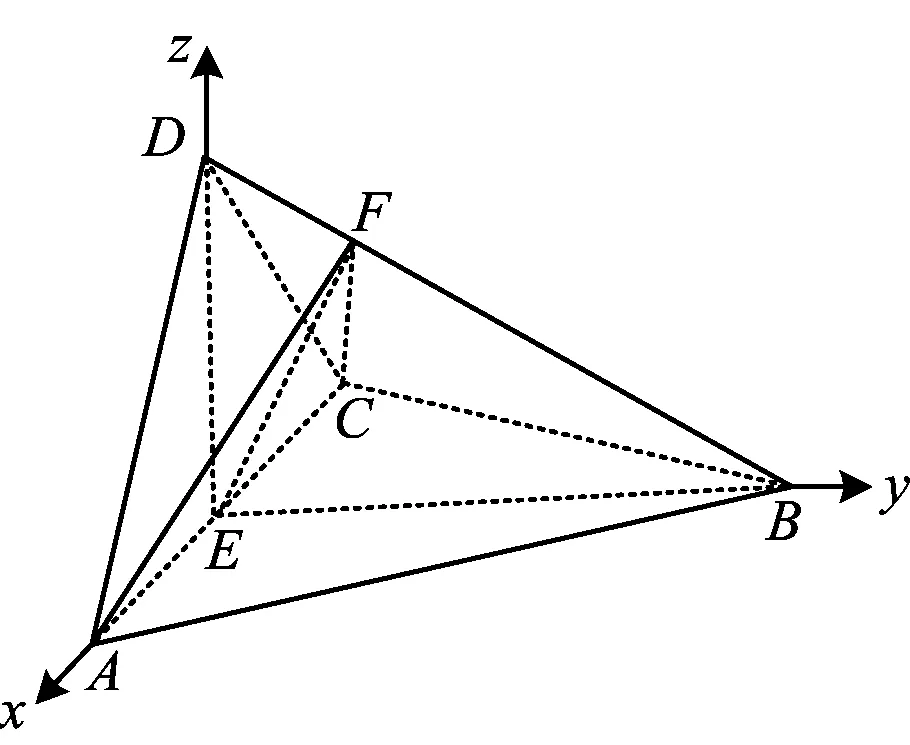
图3

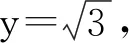
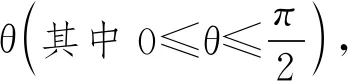
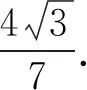
例4如图4，PO是三棱锥P-ABC的高，PA=PB，AB⊥AC，E是PB的中点．

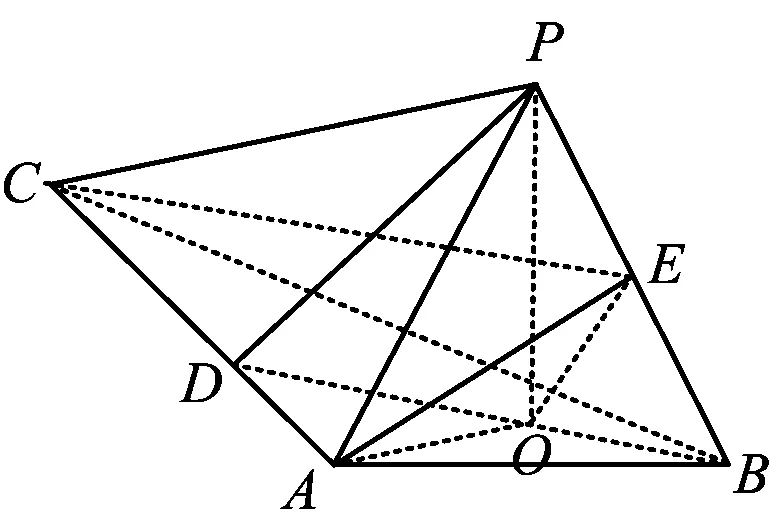
图4

1)求证：OE∥平面PAC；

2)若∠ABO=∠CBO=30°，PO=3，PA=5，求二面角C-AE-B的正弦值．

(2022年全国数学新高考Ⅱ卷第20题)

分析本题以三棱锥为载体，第1)小题考查线面平行，需要用到线面垂直的性质、三角形全等、等量代换、三角形中位线性质等知识，步骤较多；第2)小题过点A作Az∥OP，如图5建立平面直角坐标系，利用空间向量法求出二面角的余弦值，再根据同角三角函数的基本关系计算可得.

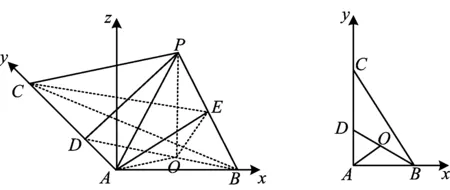
图5

1)证明如图4，联结BO并延长交AC于点D，联结OA,PD.因为PO是三棱锥P-ABC的高，所以PO⊥平面ABC，又AO,BO⊂平面ABC，从而

PO⊥AO,PO⊥BO.

因为

PA=PB，

所以

△POA≌△POB，

即

OA=OB，

亦即

∠OAB=∠OBA.

又

AB⊥AC，

即

∠BAC=90°，

从而∠OAB+∠OAD=90°， ∠OBA+∠ODA=90°，

于是

∠ODA=∠OAD,

进而

AO=DO，

即

AO=DO=OB，

故O为BD的中点.由E为PB的中点知OE∥PD，又OE⊄平面PAC，PD⊂平面PAC，因此OE∥平面PAC.

2)解过点A作Az∥OP，如图5建立空间直角坐标系.因为PO=3，AP=5，所以

又

∠OBA=∠OBC=30°，

从而

BD=2OA=8，

于是

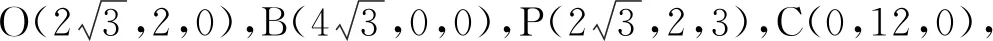
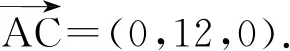
设平面AEB的法向量为n=(x,y,z)，则

令z=2，则y=-3，x=0，故n=(0,-3,2).设平面AEC的法向量为m=(a,b,c)，则

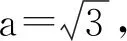
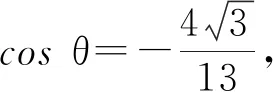
3 研究建议

1)充分利用实物模型或计算机呈现空间几何体，建立空间几何体结构意识，画好空间几何体示意图，重点提升直观想象、数学抽象素养.

立体几何初步的教学重点是帮助学生逐步形成空间观念，应遵循从整体到局部、从具体到抽象的原则[1].教材编排也按照整体到局部的安排，由基本立体图形→简单几何体的表面积与体积→空间点、线、面之间的位置关系→空间直线、平面的平行→空间直线、平面的垂直[2];空间的几何体→直线与直线、直线与平面的位置关系→平面与平面的位置关系→简单几何体的表面积和体积[3].对教师而言，教学中可提供丰富的实物模型或利用计算机呈现空间几何体，帮助学生建立空间几何体的结构及空间意识，指导学生画好空间几何体示意图，提升其直观想象、数学抽象素养.

2)熟练掌握初中平面几何知识，内化高中线面(面面)平行与垂直的判定、性质定理，有条理、规范地书写，重点提升逻辑推理素养.

立体几何解答题第1)小题的证明中用到较多初中平面几何知识，立体几何的证明(几何法)归根到底是通过降维转化为平面几何的证明，因此平行的证明多涉及三角形中位线定理、平行四边形性质等，垂直的证明多涉及勾股定理、等腰、等边三角形中线性质、菱形的对角线性质以及正方形、长方形边的关系等.另外，由三角形全等可得对应边、角相等，由三角形相似可得对应角相等、对应边成比例等.教师在教学中要时常提醒学生复习这些知识，说明其为证明过程的“血肉”，高中线面(面面)平行与垂直的判定、性质定理为“骨架”，再进行有条理以及符号语言的规范书写即可完美拿分.

3)认真分析，合理推理、计算建系，精准书写点及向量坐标，准确进行空间向量坐标运算，重点提升数学运算素养.

立体几何解答题第2)小题的夹角度量重点在于建系和点、向量的坐标书写以及向量运算.在建系时要认真分析题目，看是否有建系条件，即是否存在三垂直，否则就要进行推理、计算寻找建系条件.从题量看，9道解答题中有3道都属于不能直接建系需要推理及适当计算才能建系的类型.在点的坐标书写方面，有需要时可单画出某一平面的示意图，有利于空间点及向量坐标的书写.另外，在进行空间向量坐标运算中，要求计算准确，结论明确，从而形成解决度量问题的程序思想，重点提升数学运算素养.