基于高考试题的数学课堂教学情境创设实践研究

贾志国

【摘要】教育改革发展推动高考内容优化，高考内容逐渐走向现实社会发展需要，而不再一味强调学生数学学习技巧掌握情况，高考对学生综合素质评价的作用愈加显现.另外，“中国高考评价体系”“一核”“四层”“四翼”内容的确定，推动高考教育改革不断落实完善，关于高考相关内容的研究备受重视.如何基于数学学科情境设置，再现学科理论情景或反映现实社会问题，推动学生综合素质提升，成为高中数学学科教学不容忽视的重点.

【关键词】高中数学；高考试题；课堂教学

情境之于高考，既是价值实现的引领、素养导向的载体、能力体现的工具，也是知识考查的形式，是落实学生综合素质教育的有效手段.

笔者以高考评价体系为依据，以高中数学学科特点为前提，创设学习再现情境、学习关联情境、综合联想情境、拓展迁移情境、模型识别情境等高考数学试题情境，并基于具体试题做出解释说明.为尽量保证试题情境能够准确、有效发挥载体作用，高考数学试题情境的创设应遵循真实性、公平性、一致性和简洁性原则.

1 学习再现情境的创设

学习再现情境的创设，以学生已学课程体系内的情境型材料为主，此类材料内部关联性为学生所熟知，相应情境创设由学生直接回忆再现即可.简言之，就是让学生将已有知识、方法与试题进行关联.此情境创设方法相对简单，主要是对“四层”的考查，即对学生核心价值、学科素养、关键能力、必备知识的考查.

例1 在（1）a1+a3= b2；（2）b4= a4； （3）S5=-25，这3个条件中任选1个，在下列问题中进行补充说明，假设问题中存在y值，请进行求解，假设不存在，请说明理由.

设等差数列｛bn｝中，前n项之和为Sn，｛an｝为等比数列，，a1= b5，a2=3，a5=-81，y是否存在才会让Sy＞Sy+1且Sy+1＜Sy+2成立？

此例题考查“等差数列与等比数列”相关情境型课程知识，相应的情境创设依托等差和等比数列通项公式、前n项和公式、等差和等比数列“基本量法”“拟真推证法”等进行，而此部分内容均为学生已学内容.

因此，此例题为学习再现情境的创设，在学生基础知识考查的基础上，对学生的思维能力、探索能力、问题解决能力等进行培养，也对学生等差等比数列相关知识进行进一步的巩固复习.

2 学习关联情境的创设

学习关联情境的创设，也以学生已学课程体系内的情境型材料为主，但学生对此類材料的内部关联性了解并不完全，或学生对此的熟悉程度有所欠缺，故而要创设此类情境，既需要借助学生已掌握的知识内容，也需要学生发动脑内知识体系，通过回忆将试题与知识联想连接起来.此情境创设中复杂程度更高，也是对“四层”的考查.

例2 有一球面半径为2cm，该球面上有4点O、P、Q、M，其中OP、OQ、OM三条线之间为两两垂直关系，试求S△OPQ+S△OQM+S△OMP的最大值.

这一例题中涉及的情境型材料包括立体几何的初步学习、基本不等式等，相应的情境创设所依托的知识和方法则涉及较为广泛，包括直线和平面之间的垂直关系、长方体棱长和长方体外接球半径的关系、三元基本不等式、基本不等式求最值的方法、步形解题法等，而此部分内容与方法均为典型的回忆再现.

但这种情境创设过程中需注意以下两点：其一，三元基本不等式与三角形面积之和的最大值之间关联性并不明显；其二，长方体构造与题目具体给出的条件之间也无明显关联性.

以此为前提，就需要创设学习关联情境，基于模型“求S=12（AB.AC+AC.AD+AD.AB）的最大值”构建关系式OP2+OQ2+OM2=16，借助“基本不等式最值计算”完成题目的联想，进而才能够完成情境创设.

而这样的情境创设，在培养学生想象联想、建模思维、逻辑能力、解题能力等方面都有价值，也便于学生巩固和学习三元基本不等式等知识.

3 综合联想情境的创设

综合联想情境的创设，仍旧以学生已学课程体系内的情境型材料为主，但材料表现形式、材料内含知识、方法之间的关联，相对隐性，来源于学生已获得知识或体验.

因此，此情境的创设需要学生对相关知识有较明确的整体把握、等价转换和即景联想.此情境创设也是对“四层”的考查.

例3 现有一椭圆A，与x轴的交点为M1（-1，0），M2（1，0），与A交于点O、P的直线过M2，若|OM2|=2|M2P|，|OP|=|PM1|，则M的方程式是（  ）

（A）x22+y2=1.    （B）x23+y22=1.

（C）x24+y23=1. （D）x25+y24=1.

此例题情境型材料包括椭圆的标准方程和几何的性质两部分，材料所隐含知识直接来源于学生已有知识积累，但与椭圆定义及表达式相关的知识取决于学生更深层次的知识储备，故而解此题时需创设综合联想情境.

具体来讲，学生充分掌握了椭圆的定义，有效关联到|OM2|=2|M2P|，|OP|=|PM1|，就可由此等价转化得到新的条件|OM2|=a，|PM2|=a2，|OM1|=a，|PM1|=3a2.基于此，要求出a值，再结合|M1M2|=2，就能即景联想到余弦定理，借助△OM1M2和△PM1M2中的互补角∠OM2M1和△PM2M1来完成解题.

这样的情境创设对于培养学生数学思维、建模、运算等能力，引导学生进一步扎实知识功底有显著意义.

4 拓展迁移情境的创设

拓展迁移情境的创设，前提条件同样是已学课程体系内的情境型材料，但材料呈现方式和试题题目之间的关联性不高，对应情境创设需基于对材料的创造性解读、转换及迁移来完成，考查内容也为“四层”.

例4 已知函数f（y）=（y-1）ay，

（1）试求出f（y）的单调区间；

（2）当m>n>0时，试证明nam+m>man+n.

此例题设计中，问题（1）以学习再现情境为前提，基于对学生函数单调区间、导数与函数单调性关系等基础知识考查的同时，旨在培养学生的数学运算和问题解决能力.

问题（2）则重在考查知识点“导数在函数中的应用”，基于函数单调性与题目条件之间的不明显关联，达到情境创设目的，需要学生在解题中基于函数背景，将不等式转化为函数大小求解或比较，进而完成对表达式的am-1m>an-1n证明.

此时，学生所需要解决的问题就被转化为证明函数g（y）=ay-1y在（0，+SymboleB@）单调递增.

这一情境除了培养学生建模、求解等方面的能力，也重在培养学生的创新联系能力，让学生能够更灵活地融合知识，解答题目.

5 模型识别情境的创设

模型识别情境的创设则与学习再现情境、学习关联情境、综合联想情境、拓展迁移情境的创设有极大区别，其中主要表现在创设的前提和基础，前者以现实社会中反映社会大众现实需要的衣、食、住、行、健康、教育、休闲、自我提升等密切相关，后者则以已学课程体系内的情境型材料为主.

模型识别情境涉及的知识、方法、模型构建等旨在基于学生的知识储备，将数学知识直观化、生活化，以期解决现实问题.

模型识别情境为相对简单的生活性、实践性情境，便于学生产生“生活处处有数学”的知识现实应用意识，让学生坚定数学学习信念，引导学生学会基于数学知识解决生活问题.

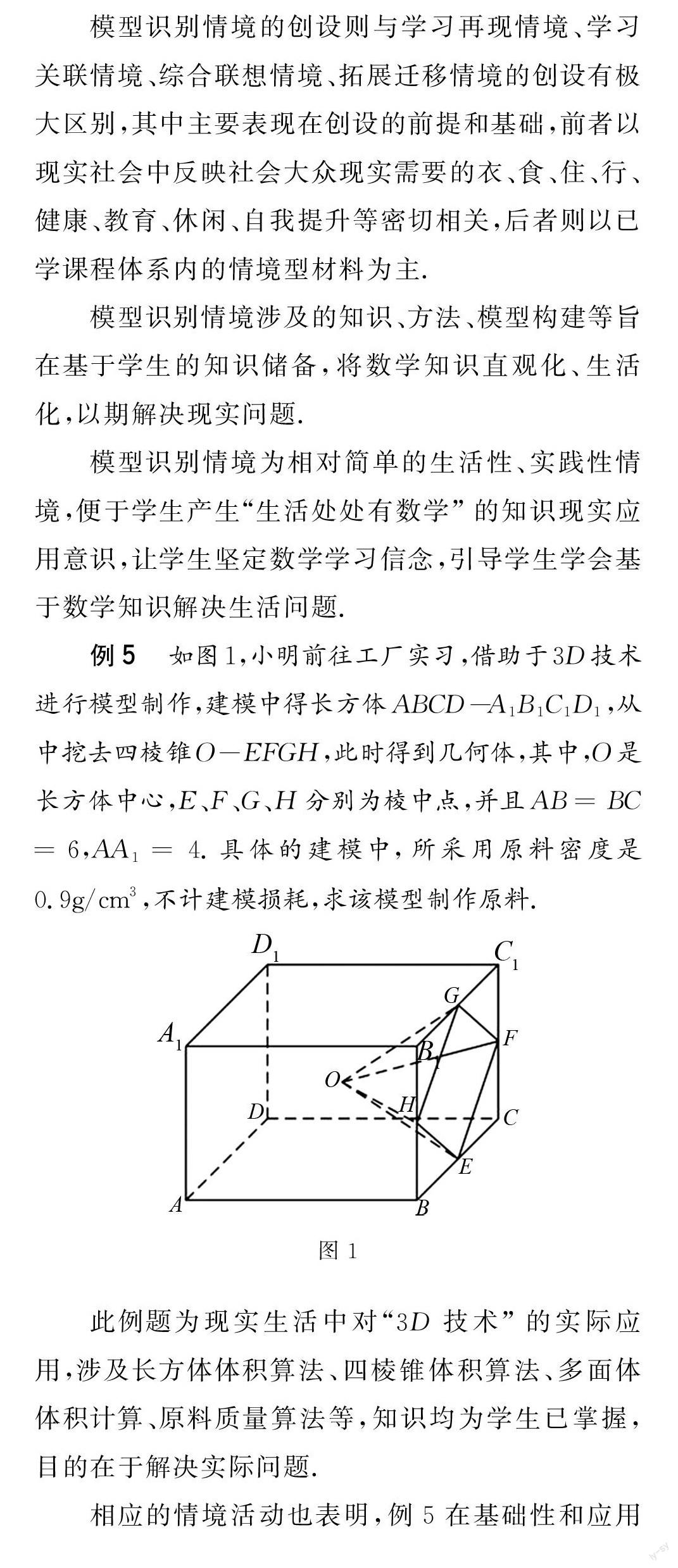
例5 如图1，小明前往工厂实习，借助于3D技术进行模型制作，建模中得长方体ABCD-A1B1C1D1，从中挖去四棱锥O-EFGH，此時得到几何体，其中，O是长方体中心，E、F、G、H分别为棱中点，并且AB=BC=6，AA1=4.具体的建模中，所采用原料密度是0.9g/cm3，不计建模损耗，求该模型制作原料.

图1

此例题为现实生活中对“3D技术”的实际应用，涉及长方体体积算法、四棱锥体积算法、多面体体积计算、原料质量算法等，知识均为学生已掌握，目的在于解决实际问题.

相应的情境活动也表明，例5在基础性和应用性的层次上考查了数学应用、数学探索等学科素养，空间想象、运算求解等关键能力，以及长方体、四棱锥的体积公式等必备知识.

6 结语

总之，教育改革发展推动考试体制改革，教育越来越强调知识的生活化应用和现实需要满足，高考题目设计也更为重视情境的创设.

基于此，教师要培养学生的数学问题解决能力，前提就是熟悉当前的考试试题情境创设类型，并系统化将这些内容应用于课题教学实践，培养学生的情境应用能力，让学生能够准确判断试题情境的类型、前提、方法内容与题目条件的关联深度等，以期能够及时完成试题解答，既提升学生的知识应用能力，落实高考评价体系的“一核四层四翼”，也进一步实现现代教育的综合发展，为打造更多全面型人才奠定现实基础.

参考文献：

[1]刘子丽，谢发超.高考数学试题情境分析与教学建议——以2020年高考数学全国卷Ⅱ理科为例[J].教育科学论坛，2022（04）：40-42.

[2]陈小波.几何特征：高考“情境化试题”解题思路的来源——以2021年全国数学高考卷Ⅰ第19题为例[J].中学教研（数学），2021（09）：43-46.

[3]羌达勋.基于“一核四层四翼”高考评价体系的试题情境分析——以2021年高考模拟演练数学卷为例[J].中学数学月刊，2021（06）：59-61.

[4]刘太涛，郑传远.高考数学三类情境下的试题评析及教学建议——以2020年高考数学试题为例[J].中学数学研究（华南师范大学版），2021（08）：45-47.

[5]谢榕平.高考评价体系下以情境为载体的数学试题及备考策略研究[J].理科考试研究，2021，28（01）：2-4.

[6]张景信，廖光及，林剑.情境视角下的高考数学试题分析与思考——以2017-2019年全国数学Ⅰ卷理科为例[J].理科考试研究，2020，2）：2-5.