矩阵摄动和Newmark-β逐步积分相结合的不确定性结构载荷识别

李晓旺， 黄 科， 魏广威， 杨翔飞， 黄 磊

(北京机械设备研究所，北京 100854)

1 引 言

动载荷识别[1]是结构动力学研究中的第二类逆问题，即已知系统特性和输出响应反求输入激励。快速准确获取结构的受力情况可以为结构的健康监测提供重要参考。对于确定性结构的载荷识别已经涌现出大量算法，归纳起来主要有频域法[2-4]、时域法[5-7]以及智能算法[8,9]。然而，在实际工程中也存在较多不确定性现象。这些不确定性与材料的理化性能、几何特性、边界条件、测量误差和分析模型等因素有关。如在工程实际中某个梁或桁架制造完成后发现原材料内部存在细微缺陷，或者工作人员在制作过程中对长度和外径等尺寸测量不准确。在这些情况下，就需要将结构对应的物理参数或尺寸参数作为不确定性参数来处理[10]。

目前专门针对不确定性结构进行的载荷识别工作还比较少，现有的识别算法主要分为两种思路，即蒙特卡洛模拟[11]和摄动理论[12-13]。蒙特卡洛模拟是最早出现的处理不确定性的方法，其原理简单，只需要在区间范围内对不确定参数大量重复采样，对每一个采样点计算，最终获得载荷的最大值和最小值。蒙特卡洛模拟的缺点是计算量过大，运算效率极低。孙兴盛等[13]将所求载荷在不确定性参数的邻域内展开成一阶级数，分别计算载荷中值和一阶摄动量，从而建立了针对不确定性结构进行激励反演的矩阵摄动方法。然而，该摄动方法需要对载荷时间历程的每一个时刻都计算一次中值和摄动值。由于在时域内动态激励的时间历程一般都含有大量时间步，因此会导致迭代步骤过多，运算量较大。

为了弥补现有的不确定性结构载荷识别方法存在的不足，本文在时域内建立了一种矩阵摄动和Newmark-β逐步积分相结合的算法。首先借助矩阵摄动理论将动态载荷表示成中值和一阶摄动量叠加的形式，然后引入Newmark-β逐步积分法分别反求载荷中值和一阶摄动值，最后将载荷中值与一阶摄动值进行加减运算，从而确定动态激励的上下界。仿真算例验证了该方法能够高效准确地反演出载荷边界，并有力抵御噪声干扰。

2 载荷识别算法

2.1 Newmark-β逐步积分算法

对于一个多自由度线弹性结构，振动微分方程为

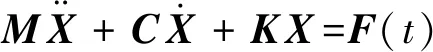
(1)

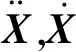
假设阻尼形式为瑞利阻尼[14]，则阻尼矩阵可以表示为

C=c1M+c2K

(2)

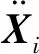
(0≤γ≤1)

(3)

(0≤β≤0.5)

(4)

ti + 1时刻的速度和位移可以表示为

(5)

(6)

将式(3)代入式(5)可得

(7)

将式(4)代入式(6)可得

(8)

对式(8)变形可得

(9)

将式(9)代入式(7)可得

(10)

将式(9，10)代入式(11)得

(11)

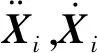
(12)

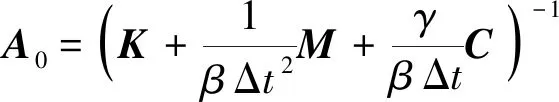
(13)

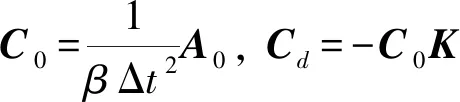
Cv=-C0(C+ΔtK)

(14)

将式(12～14)结合起来可得

(15)

(16)

令

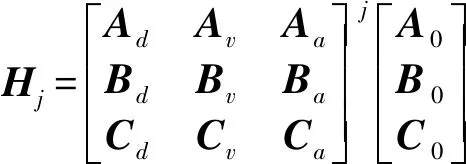
(17)

式(16)可以简化成振动离散方程为

Y=HF

(18)

式中

由于矩阵不适定的存在，在获得振动离散方程之后，采用Tikhonov正则化技术[15]重构式(18)的输入载荷F。设系统误差e为

e=Y-HF

(19)

引入罚函数的概念J为

J=(eHe)+λ(FHF)

(20)

当J对F的一阶导数为0，误差e达到最小值。此时激励F可以表示为

F=(HHH+λI)-1HHY

(21)

式中I为单位矩阵，λ为正则化参数，正则化参数的值借助L曲线法[16]计算获得。

2.2 矩阵摄动理论

设不确定性结构共含有k个不确定性参数，任意一个不确定性参数用bj(j=1,2,…,k)来描述，那么不确定性参数的集合向量b可以表示为

(22)

基于区间分析思想，将不确定性参数bj(j=1,2,…,k)用区间参数的形式表示，即

(j=1,2,…,k)

(23)

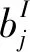
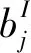
(j=1,2,…,k)

(24)

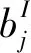
(j=1,2,…,k)

(25)

参数bj(j=1,2,…,k)的不确定性程度由不确定度uj来表征。uj越大，参数不确定性越严重，uj的计算公式为

(j=1,2,…,k)

(26)

bj(j=1,2,…,k)的摄动部分δj的范围为

(j=1,2,…,k)

(27)

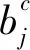
(j=1,2,…,k)

(28)

对于含有不确定性参数的振动系统来说，结构特性矩阵M,C,K以及载荷向量F(t)都不再是定常值，而是关于不确定性参数集合b的函数，那么M,C,K和F(t)可改写成M(b),C(b),K(b)和F(t,b)。

在矩阵摄动理论的推导过程中，首先需要计算结构特性矩阵和载荷向量的中值和一阶偏导。M(b),C(b),K(b)和F(t,b)在不确定性参数的中值bc处的值可表示为

M0=M(bc)，C0=C(bc)

(29，30)

K0=K(bc)，F0(t)=F(t,bc)

(31，32)

M(b)，C(b)，K(b)和F(t,b)关于任意一个不确定性参数bj(j=1,2,…,k)的一阶偏导数在bc处的值可表示为

M1,j=∂M(bc)/(∂bj)

(j=1,2,…,k)

(33)

C1,j=∂C(bc)/(∂bj)

(j=1,2,…,k)

(34)

K1,j=∂K(bc)/(∂bj)

(j=1,2,…,k)

(35)

F1,j(t)=∂F(t,bc)/(∂bj)

(j=1,2,…,k)

(36)

在计算得到特征矩阵和载荷向量的中值和一阶偏导之后，可以将M(b)，C(b)，K(b)和F(t,b)在bc的邻域处近似表示为一阶泰勒多项式展开式为

(37)

(38)

(39)

(40)

以上即为结构动力学的矩阵摄动公式，将上述四个一阶泰勒多项式代入振动微分方程(1)，可得

(41)

由于所有不确定性参数之间互不相关，所以式(41)成立的条件是每一个求和项均为0，即

(42)

(43)

式(42，43)与振动微分方程式(1)具有相似的形式，可借助2.1节的Newmark-β逐步积分的载荷幅值识别算法重构F0(t)和F1,j(t)(j=1,2,…,k)的时间历程。最后通过矩阵摄动公式将以上两部分相加减，即可获得动态激励的上下边界为

(44)

(45)

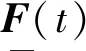
3 数值算例分析

为证明本文载荷识别算法的可行性和有效性，建立了2个含有不确定性参数的数值算例。每个算例中借助位移传感器测量节点的位移响应作为已知条件，然后采用本文算法分别对2个算例的动态激励时间历程上下界进行重构，并和传统的蒙特卡洛法进行对比。

3.1 渐变式载荷识别

算例1建立一个悬臂梁模型如图1所示，载荷施加在节点8，位移传感器分别位于节点7和节点10。

悬臂梁各项参数分别为

(1) 不确定性参数。弹性模量E=[68,72] GPa。

(2) 固定参数。泊松比0.33，密度2700×103kg/m3，长宽高尺寸为1000 mm×50 mm×20 mm。

对悬臂梁模型施加1个时间历程变化比较平缓的时变载荷F1，F1的时间历程如图4所示。

图1 受渐变式载荷激励的悬臂梁模型Fig.1 Cantilever beam model with slowly changing excitation

在算法实施前需要进行两步前处理，第一步通过仿真方式获得节点动态响应，第二步在动态响应中加入5%的高斯白噪声。前处理完成后采用本文算法识别动态激励F1的中值以及关于不确定性参数E的一阶偏导数，识别结果如图2和图3所示。

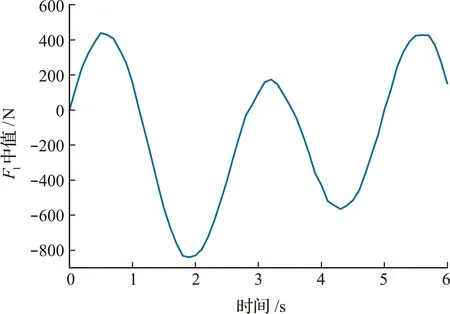
图2 F1中值识别结果Fig.2 Midpoint value identification result of F1

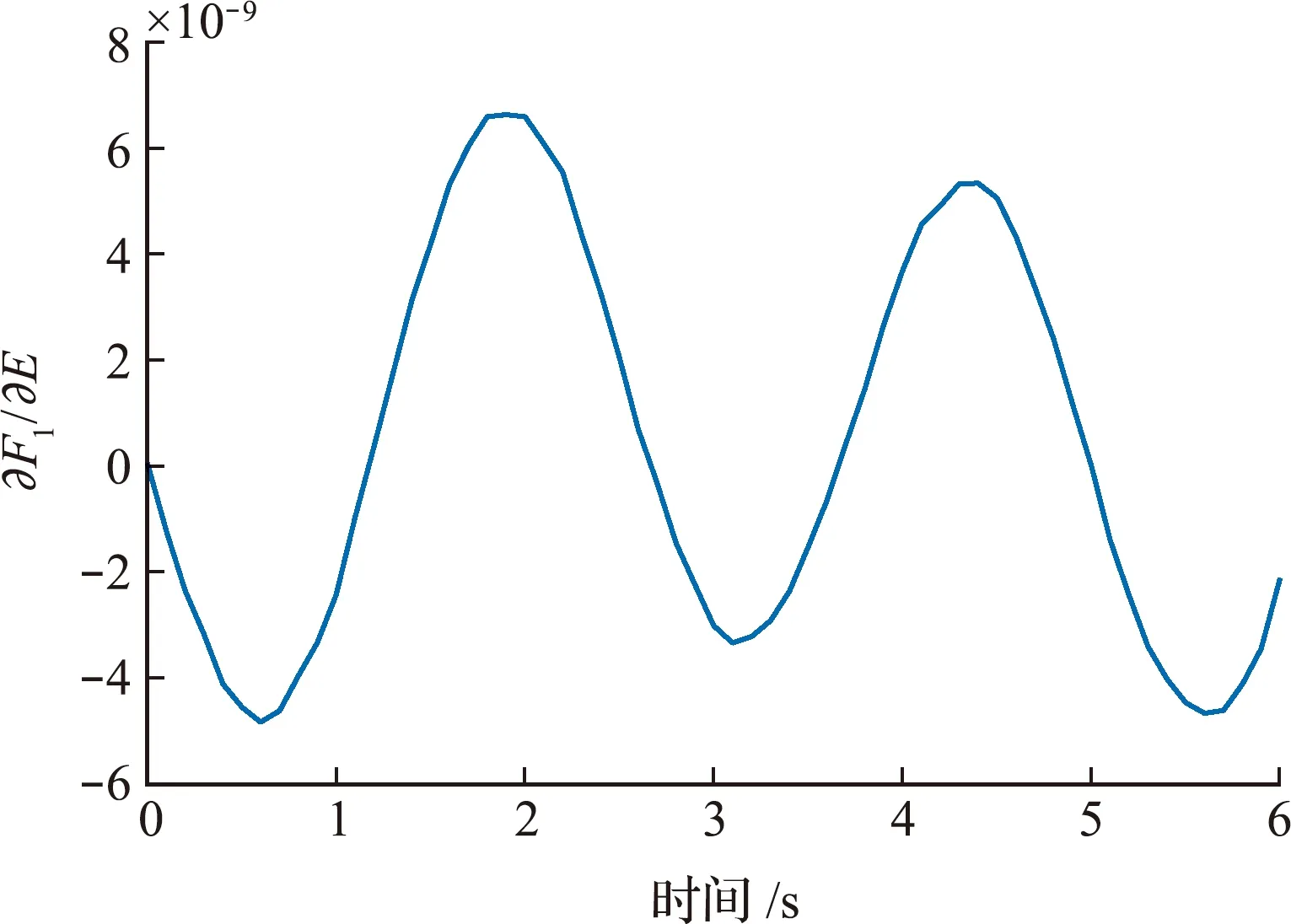
图3 ∂F1/∂E的识别结果Fig.3 Identification result of ∂F1/∂E

在获得F1的中值以及关于E的一阶偏导数的前提下，根据式(44,45)计算F1的上下边界。同时，蒙特卡洛法也反演F1的上下边界作为对照。两种算法对F1的识别结果如图4所示。同时，为了定量分析算法的精确度，选取了5个有代表性的时间点计算对应的识别误差，计算结果列入表1。

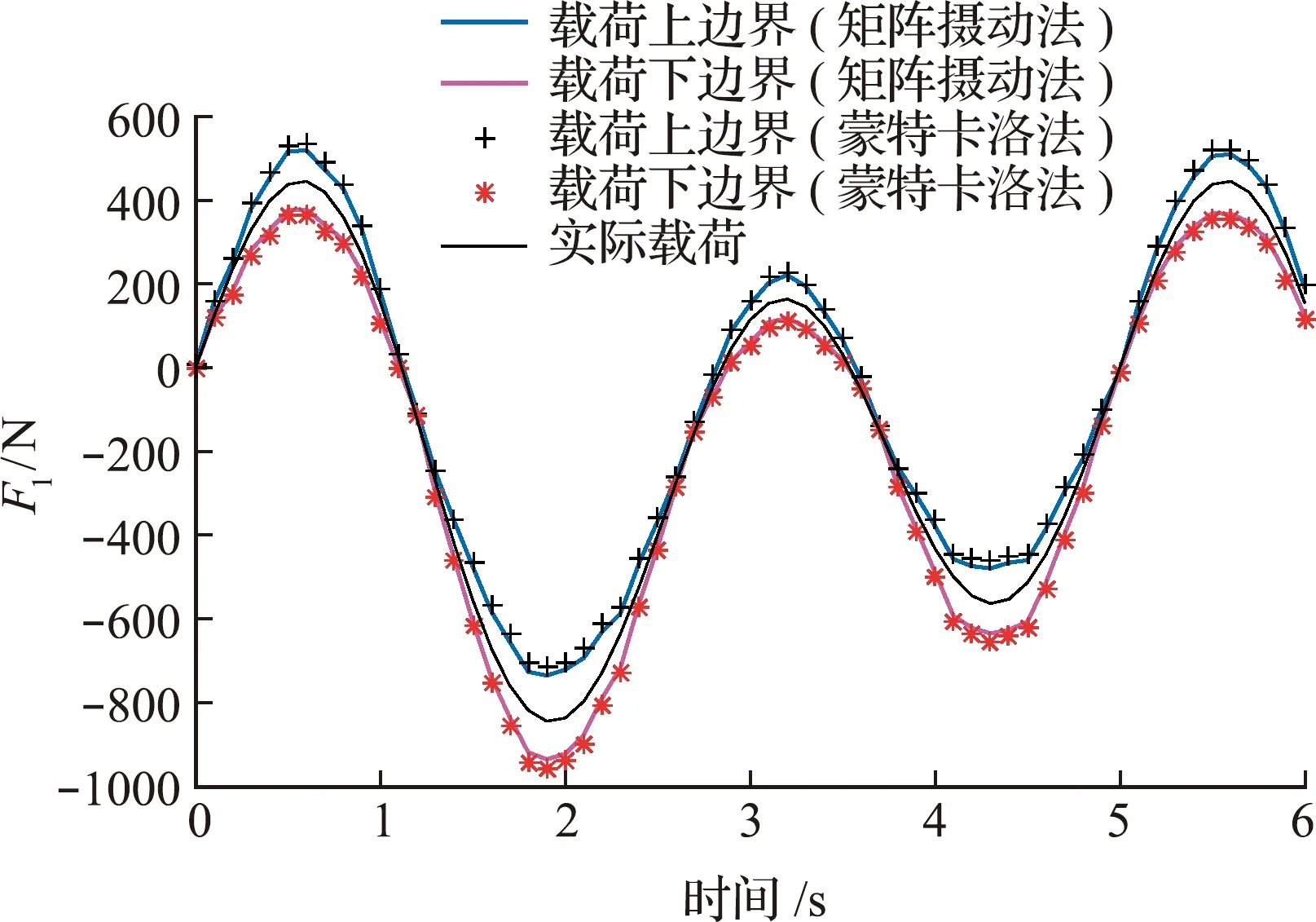
图4 F1识别结果Fig.4 Identification result of F1

表1 算例1中F1的上下界偏移量Tab.1 Offset of identified load F1 in Example 1

从图4可以看出，通过本文算法识别出的载荷上下边界可以准确地将F1的实际值包含在内，体现了算法的有效性。同时，本文算法识别的载荷边界与蒙特卡洛法的识别结果吻合度较好，说明算法的识别精度较高。由于受到5%噪声的影响，识别的动态激励在一些时间点上有轻微波动，但总体时间历程保持平稳，显示出较强的抗噪性能。由表1可知，F1重建边界的最大偏移量和最小偏移量分别为25.54%和10.21%。作为对照，蒙特卡洛法的识别误差比矩阵摄动法稍高但相差不大。

3.2 突变式载荷识别

算例2建立一个桁架模型，载荷和位移传感器的位置如图5所示，其中3个位移传感器所测信号均为节点的竖直位移信号。

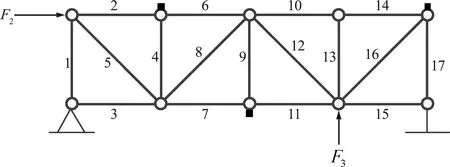
图5 受突变式载荷激励的桁架模型Fig.5 Truss model with rapidly changing excitation

桁架的各项参数如下。

(1) 不确定性参数。4号桁架的长度l=[599,601] mm，11号桁架的直径d=[19.5,20.5] mm。

(2) 固定参数。弹性模量200 GPa，泊松比 0.3，密度7800×103kg/m3，除4号桁架以外的所有水平和竖直桁架的长度为600 mm，除11号桁架以外的所有桁架直径为20 mm。

对悬臂梁模型施加2个时间历程变化比较迅速的突变式载荷F2和F3,F2和F3的时间历程如图6所示。

前处理过程首先通过仿真方式获得节点动态响应，然后在响应信号中加入10%的高斯白噪声。前处理完成后采用本文算法反演动态激励F2和F3的中值以及关于不确定性参数l和d的一阶偏导数，识别结果如图6～图8所示。

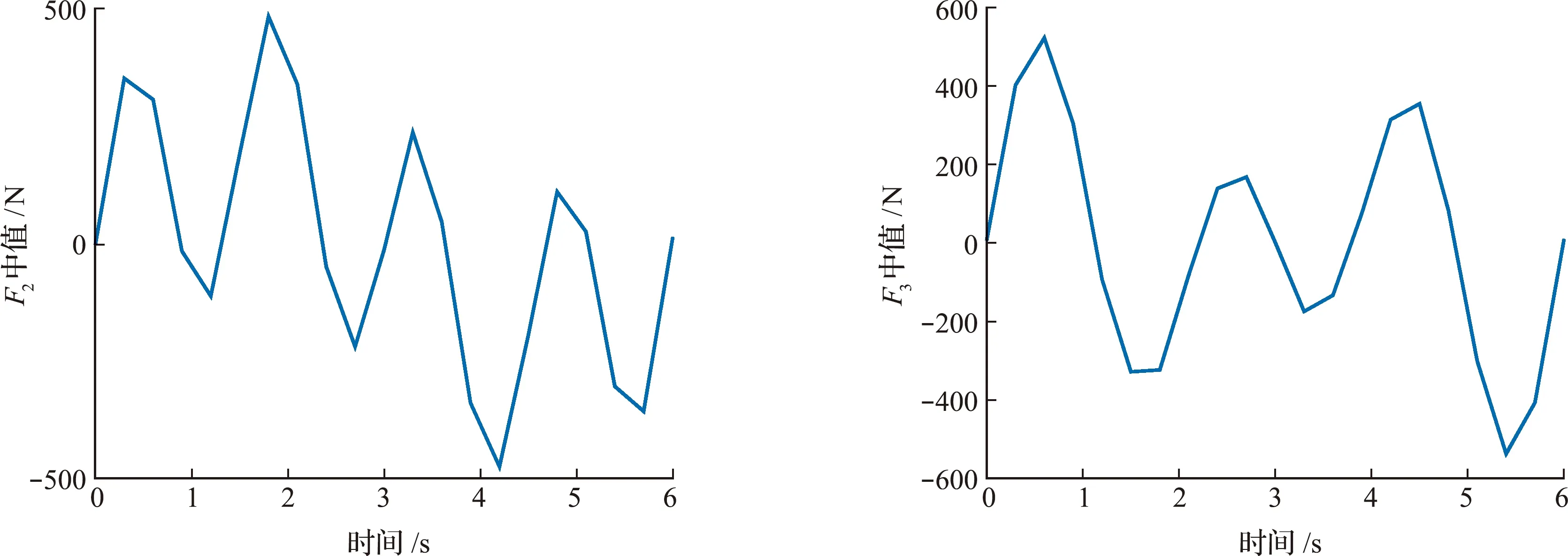
图6 F2和F3的中值识别结果Fig.6 Midpoint value identification results of F2 and F3

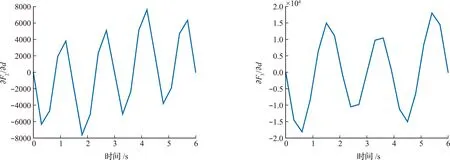
图7 ∂F2/∂d和∂F3/∂d的识别结果Fig.7 Identification results of ∂F2/∂d and ∂F3/∂d

图8 ∂F2/∂l和∂F3/∂l的识别结果Fig.8 Identification results of ∂F2/∂l and ∂F3/∂l

在求得F2和F3的中值以及二阶偏导数之后，分别采用本文算法推导的式(44，45)以及对照蒙特卡洛法反演F2和F3的上下边界，两种算法识别的F2和F3的上下边界如图9所示。同时，为了更加直观地分析算法精度，选取了5个时间点计算识别结果和真实值的相对误差，误差的计算结果列入表2和表3。

算例2的突变式载荷在时间历程上比算例1的渐变式载荷更复杂，不确定性参数增多，噪声水平也更高。从图9可以看出，识别的动态激励F2和F3的上下界仍保持鲁棒性并将实际载荷包络在内。同时，本文算法和蒙特卡洛法反演的载荷边界基本保持一致，体现了较高的识别精度。由表2和表3可知，F2的最大和最小偏移量值分别为 23.09% 和 2.33%，F3的最大和最小偏移量值分别为34.29%和12.25%。总体来看，本文算法识别载荷边界的偏移量值在各时间点上接近于蒙特卡洛法的偏移量值，证明本文方法重建的激励上下界合理有效。

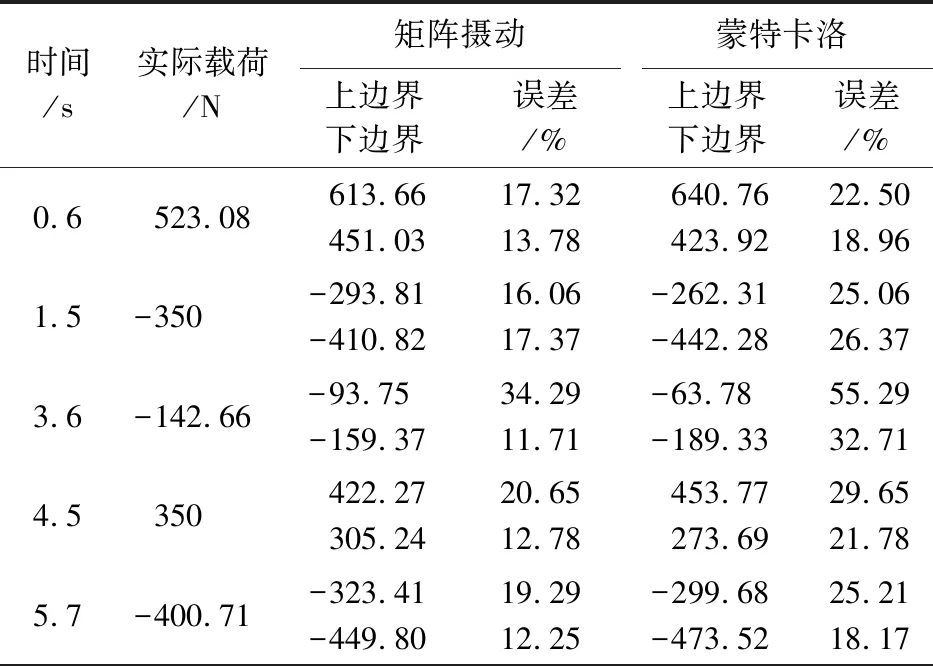
表3 算例2中F3的上下界偏移量Tab.3 Offset of identified load F3 in Example 2

图9 F2和F3的识别结果Fig.9 Identification results of F2 and F3

4 结 论

针对含不确定性参数结构的动载荷识别问题，本文在时域内推导了一个将矩阵摄动理论和Newmark-β逐步积分法结合起来的综合算法，该算法具有如下优势。

(1) 通过矩阵摄动理论将动载荷表示成中值和摄动量相加的一阶泰勒展开式，避免了在不确定性参数的区间内大量采样计算，显著提高了运算效率。

(2) 在计算载荷中值和摄动量时引入了Newmark-β逐步积分法并进行了改进，改进之后的Newmark-β逐步积分法本质上是无条件稳定而在形式上是一个简单的线性离散方程，从而在不影响求解精度的同时又省略了复杂的时间步迭代。

数值算例结果证明，对于复杂程度不同的载荷以及不同的噪声水平，该方法均可以高效准确地反演出载荷上下边界，显示出了较高的识别精度，并具有较强的鲁棒性和抗噪性。