复杂微通道气体流动的格子Boltzmann模拟
姚 杰, 董 波, 李维仲
(大连理工大学 海洋能源利用与节能教育部重点实验室,大连 116024)
1 引 言
目前,在油气开采[1-3]和微机电装置[4]等领域普遍存在的微通道内气体流动现象受到广泛关注。在微通道中,由于特征长度H很小,能达到微米级甚至纳米级,气体分子平均自由程λ通常为10-7m~10-8m(以甲烷分子为例,273 K和0.1 MPa时,λ=0.058 μm),此时努森数Kn=λ/H>10-3,流动处于滑移区,在研究中需要考虑努森层对流动的影响。努森层是气体流经壁面时在近壁面处存在的一个局部非平衡区。在努森层内,气体密度较小,分子间碰撞相对较少,流体的动力学行为主要受气体分子和固壁之间的碰撞影响,流体粘度显著降低。由于固壁作用,近壁面气体速度不同于壁面速度,这意味着会出现流动不连续或速度滑移。此时流体不能按照连续介质处理,基于连续介质假设的N-S(Navier-Stokes)方程组不能描述气体流动状态。
通常,当流动处于滑移区(10-3≤Kn≤0.1)时,在努森层影响下,气体流动状态可以用N-S方程加滑移边界来描述,N-S方程组依旧可以很好地描述主流区内流体流动。当流动处于过渡区(0.1 格子Boltzmann方法(LBM)是一种基于分子动理论的介观数值模拟方法,计算效率高,且易于处理复杂边界,尤其适用于孔隙尺度内流动模拟[10]。目前已有学者利用LBM研究微气体流动问题。Zhao等[1]建立了一个微尺度多松弛时间LB模型,用于模拟气体在各向异性多孔介质中的流动。姚军等[3]采用考虑正则化过程的微尺度LB模型研究微裂缝对致密多孔介质中气体渗流的影响机制。上述研究采用的动力学边界Maxwell反射边界是一个完全漫反射边界[11],模拟时得到的滑移速度会比实际滑移速度大。Chai等[12]将Maxwell漫反射边界与半步长反弹结合提出了新的曲面滑移边界,可用于复杂微通道气体流动。Chen等[13]提出了考虑Klinkenberg效应的表征单元体尺度LB模型,并采用该模型研究了微裂缝对页岩气渗流的影响。Suga等[10,14]讨论了微尺度LB模型在Poiseuille流、Couette流和组合微通道流等算例中的应用,并对比了采用不同离散速度,边界条件模型的计算结果。以上采用的模型没有考虑孔隙截面变化带来的Kn数的变化。 尽管前人已经利用LBM对气体微流动进行了大量研究,但是采用模型仍具有一定局限性。实际多孔介质中,孔隙结构蜿蜒变化,交错纵横,因此孔隙内部各点的特征尺寸也不一样,且对于含有微缝隙的介质,特征尺寸跨度很大。由于孔隙的特征尺寸与Kn数息息相关,而Kn数又决定着流体流动状态,因而采用单一特征Kn数来代表整个多孔介质内每一点的Kn数势必会带来较大的误差。 本文建立了适用于微通道气体流动的多松弛格子Boltzmann模型,考虑了努森层内分子平均自由程的修正,采用半步长反弹和Maxwell漫反射边界组合的曲面边界格式,将局部Kn数引入演化方程。该模型可以模拟滑移区和过渡区的渗流问题。 格子Boltzmann方程(LBE)可以看作Boltzmann方程的一种离散格式[15,16],且已证明是研究微尺度流动的有效工具[17-20]。演化方程为 fi(x+ciδt,t+δt)-fi(x,t)=Ωi(f)+δtFi (i=0,1,…,b-1)(1) 式中fi(x,t)为速度为ci的气体分子在时刻t空间位置x处的分布函数;Fi为系统受到的体积力的源项,δt为时间步长,b为空间的离散方向数,对于D2Q9模型,b=9。离散速度为 (2) 式中c=δx/δt为格子速度,本文c=1。Ωi(f)为离散的碰撞算子,且对于LBGK模型[21]为 (3) (4) (5) LBGK模型在很多领域得到广泛的应用,然而最近的一些研究指出LBGK模型在计算气体微流动具有一定局限性[22],主要在于应用动力学边界时会引入非物理因素。根据气体动理论,滑移速度us只取决于Kn数以及气体与壁面的相互作用系数,但是在LBGK模型中,滑移速度还和网格分辨率相关。而多松弛模型(MRT)则可以通过选择合适的松弛时间避免这种非物理因素的干扰。因此本文采用多松弛(MRT)模型碰撞算子[23]为 (6) 式中M为一个b×b阶转换矩阵,用于将速度空间的分布函数fi投影到矩空间m=Mf,其中f=(f0,f1,…,fb - 1)T,S=diag(τ0,τ1,…,τb - 1)-1为非负对角矩阵,τi为第i个矩的松弛时间。转换矩阵为 (7) 对应的松弛矩阵 (8) 式(1)的演化过程可以写作两步为 碰撞 (9) 迁移 (10) 离散的外力源项Fi可表示[24]为 (11) (12) 式中G为系统受到的体积力的合力。 2.2.1 松弛时间 在LBM中,宏观尺度下流动特征参数是雷诺数,通常由Re数来确定松弛时间;而对于微尺度下的气体流动,特征参数是努森数,需要通过Kn数来确定松弛时间。由分子动理论以及格子Boltzmann方法中粘度与松弛时间的关系可推得松弛时间τ与Kn数的基本关系式为 (13) 式中N为模型中特征尺寸所占的网格数。由于努森层的存在,微通道系统中近壁面处气体的运动是受限的,分子平均自由程小于远离壁面处分子的平均自由程。开放系统和无边界系统中分子平均自由程的关系为[25] (14) 式(14)表明,受限程度随Kn数的变大而显著。当Kn数趋于0,也就是努森层占比很小时,此时有效平均自由程又恢复到开放系统的平均自由程。 将有效平均自由程代替平均自由程以修正Kn数较大时努森层对主流层的影响,可以在Kn数变化更大的范围内模拟气体的微流动现象。因此,本文微通道中流体流动的MRT模型的松弛时间为 (15) 其他参数可取τe=1.0,τe=τε=1/1.4,τd=1.0,τq的取值和滑移边界相关。 2.2.2 曲面滑移边界 将滑移边界引入到LBM的方法主要有两种。第一种方法是用滑移速度来反映边界处滑移长度的影响[26]。第二种方法是采用组合滑移格式。对于处于滑移区的气体流动,可采用LBM边界包括镜面反射(SR)、标准反弹(BB)和麦克斯韦漫反射(MD)等格式组合的混合格式[12]。根据计算需要,本文采用MD和BB的组合格式。该格式具有清晰的物理意义,即运动到固壁的气体分子,一部分直接反弹回去,另一部分与固壁相互作用并达到Maxwell平衡分布再反射回去。在原格式的基础上,考虑努森层以及局部Kn数的影响。曲面滑移边界可表示为 (16) (17) 根据具有解析解的平板Poiseuille流求取组合系数r。MRT-LBM结合式(16)可推得近壁面相邻流层速度之间的关系[12]为 u2=Au1+Bδta (18) 式中 系数A和B为 A=(3-2r+rτs)/(1-r+rτs) (19) B=[(11/2-2τq-8τs+4τqτs)r+4τq+4τs- 8τqτs-5]/[(2τs-1)(1-r+rτs)] (20) Poiseuille流的解析解为 u=(4U0y/H)(1-y/H)+us (21) 式中y=(j-Δ)δx。对于半步长反弹,Δ=1/2,可得两流层之间的速度关系式。 u1=(2u0δx/H)[(2H-δx)/(2H)]+us u2=(6u0δx/H)[(2H-3δx)/(2H)]+us (22) 代入式(18),并令ε=δx/H,可得 (23) 联立式(19,23),可得 us/u0=[(2r-2)(1-2τs)/(1+r)]ε+ {[16(τq-0.5)(τs-0.5)-3]/3}ε2 (24) 此速度是根据滑移边界条件求得的滑移速度,与实际滑移速度比较即可得到组合系数r。实际平板Poiseuille流滑移速度可表示为[23] Us=4C1Kn+8C2Kn2 (25) (26) 多孔介质是由固体骨架和相互连通的孔隙所构成,孔隙内部各点的特征尺寸也不一样,且对于含有微缝隙的材料,特征尺寸跨度很大。Zhao等[1]提出了一个获取孔隙特征尺寸的方法,通过边缘细化算法[27,28]提取孔隙中轴,然后根据获取的孔隙中轴计算孔隙的局部特征尺寸。经细化算法处理后的多孔介质如图1所示。对于每一个中轴点,该点处的特征尺寸为中轴点到最近固壁距离的2倍。这样便得到了孔隙内任意的特征尺寸H(r)。 选取合适的参考特征尺寸Href、参考压力Pref和参考温度Tref,可确定参考努森数Knref,则局部努森数Kn(r,t)可表示为孔隙内某一点温度T(r,t)、压力P(r,t)以及特征尺寸H(r)的函数,可表示为 (27) 代入式(15),可得局部松弛时间 (28) 图1 边缘细化算法获取中轴Fig.1 Central axis obtained by edge thinning algorithm 为了验证所构建模型的正确性,本文采用Poiseuille流对模型在过渡区以及滑移区的计算滑移速度准确性进行验证。 平板长度为L,宽为H,区域网格为100×15,上下边界为固体节点,左右边界为周期性边界,固体边界采用滑移边界,令σ=1.0,即固壁是全反射的。水平方向添加外力场Fx=5×10-5,由式(11)引入模型中,收敛条件为 (29) 式中ux和uy分别为通道中气体沿x方向和y方向的流动速度。 本文对不同Kn数下的气体流动情况进行模拟,将模拟结果与直接模拟蒙特卡洛方法(DSMC)、信息保存-直接模拟蒙特卡洛方法(IP -DSMC)[29]以及未进行有效平均自由程修正和边界采用DBB格式[30]的计算结果进行比较。当模拟达到稳态后,统计x=L/2处的无因次速度分布如图2所示。 图2 不同Kn数下Poiseuille流无因次速度分布Fig.2 Dimensionless velocity profile comparisons of Poiseuille flows under different Kn numbers 本文在滑移区和过渡区模拟结果与平板滑移模型解析解吻合较好。当Kn数较小时,不采用有效平均自由程修正的LBM结果与解析解和DSMC方法的解吻合较好,但是在Kn数较大的过渡区,其滑移速度偏小,这是因为努森层占主流区比例变大,壁面对流动影响愈加明显,此时表观滑移速度将明显小于实际滑移速度。这与本文分析结果一致,且进一步证明有效平均自由程修正的必要性。 应用本文提出的模型研究气体在各向异性多孔介质中的流动,如图3所示。模拟区域为400×300,其中孔隙率ε=0.597,孔隙实际物理尺寸为7.5 μm~0.5 μm。孔隙中流动的气体为273 K和0.1 MPa状态下的甲烷,对应局部Kn数范围为0.0077~0.116,平均努森数Knm=0.0192。本文通过改变网格分辨率来调整Kn的数值。由达西定律 k=μ·Q·ΔL/(A·ΔP) (30) 图3 多孔介质Fig.3 Porous media 式中Q为体积流量,A为通道的截面积,对于二维模型,A=Ly,μ为气体的动力粘度。对于本算例,体积流量Q的计算式为 Q=∑uxδy (31) Knm平均努森数可计算为 Knm=∑Kn(r)、N (32) 式中N为孔隙点的个数。选取模拟的Knm数范围为0.0001~3.8。 图4为稳态时多孔介质内气体无因次流速的纵向分布情况。无因次流速为孔隙中某一点的流速和孔隙最大流速的比值,可以反映在Knm数变化时孔隙内流速分布的变化情况。 图4 孔隙内无因次速度分布情况Fig.4 Dimensionless velocity distribution in pores 可以看出,当Knm数较小时(图4(a)),多孔介质中主流通道较少,此时气体主要流经相对大的孔隙,多孔介质的非均质性对气体的流动影响明显;而随着Kn数的增加,小孔隙中的气体流动受努森层的影响变大,相对大孔隙而言,小孔隙内的气体流速增加,主流通道明显变多(图4(f)),多孔介质的非均质性影响减弱。为了进一步研究Knm对孔隙中速度的影响,提取了不同Knm下截面x=115和x=240上的速度分布情况,如图5所示。气体的流速分布在各个截面上仍呈现近似的抛物线分布,这与Poiseuille流是一致的,随着多孔介质内Knm的增加,通道内各点的无因次速度相应变大,且可以明显看到小孔隙内气体速度增加幅度更大,孔隙愈小,增加幅度越大。这是由于小孔隙的局部Kn数更大,微尺度效应更明显。随着Knm数的增加,大孔隙和小孔隙流动阻力均减弱,小孔隙中流动阻力减小得更多。这与Klinkenberg对多孔介质内气侧渗透率大于固有渗透率且展现出压力依赖性的解释一致[31]。 图5 不同截面上流体无因次速度分布情况Fig.5 Dimensionless velocity distribution of the fluid at different cross -sections 为了研究Knm数对孔隙内渗流特性的影响,首先,将孔隙内气体的流速无因次化,然后,计算多孔介质的等效流速v=Q总/Ly,其中Q总为出口截面的体积流量,Ly为出口截面的长度。本文为了直观观察孔隙中气体的流动情况,令孔隙内速度大于等效流速的孔隙为高渗点,将孔隙分成高渗区域和低渗区域。定义高渗区域与孔隙面积的比值为多孔介质的高渗面积比R,高渗面积比随Knm数的变化如图6所示。结果表明随着Knm的增加,高渗面积比逐渐增大。 当Knm数增大时,小孔隙中高渗区域相比大孔隙增加更加明显,且小孔隙的高渗区域相比于大孔隙更靠近壁面。这是由于小孔隙中滑移速度更大,速度分布更均匀所致。 图6 高渗面积比随Knm的变化Fig.6 Variation of high permeability area ratio with Knm 在此基础上,本文分别计算在不同Knm数下孔隙表观渗透率ka,并和Klinkenberg的宏观渗透率模型的计算值进行比较,ka的表达式为 ka=k∞(1+6c·Kn) (33) 式中k∞为固有渗透率,c为相称性因子。为了便于比较,令kr=ka/k∞,用kr来表征表观渗透率的大小。对于相称性因子,取值与多孔介质有关,平板模型一般取c=1.0,对于其他多孔介质,一般c<1.0,当c=0.4,与本文算例计算结果吻合较好,这也证明了本文构建模型用于计算多孔介质的正确性。本文计算结果与Klinkenberg模型计算值的比较列入表1。 表1 不同Knm下相对表观渗透率比较Tab.1 Comparison between current results and result obtained by Klinkenberg model in terms of relative apparent permeability at different Knm (1) 考虑努森层的影响,本文构建了适用于滑移区和过渡区的MRT-LBM模型,通过算例Poiseuille流对模型进行了验证,所得结果与用直接蒙特卡洛方法和分子模拟获得的结果吻合较好。本文的模型能够较好模拟滑移区以及过渡区的气体滑移现象,并且在Kn数较大情况下(Kn>0.1),比不考虑有效分子平均自由程修正的滑移速度更加准确。 (2) 本文利用所建立的模型研究了微尺度下非均质多孔介质内气体渗流特性。结果表明多孔介质的表观渗透率随着平均努森数Knm增加而增加,这与Klinkenberg宏观渗流模型理论一致。随着Knm数的增加,小孔隙中气体渗流速度相对大孔隙内气体渗流速度有所增加,主渗流通道数增加。通过分析不同Knm数下多孔介质内高渗区域分布发现,随着Knm数增加,孔隙中高渗区域占总孔隙比例增加,且高渗区优先从小孔隙近壁面处增加,这是因为小孔隙中努森层占比更大,气体分子和壁面间碰撞所占比例增大,滑移流速增大,气体流动阻力减小,截面速度分布更加均匀。2 数值方法
2.1 适用于微通道流动模拟的格子Boltzmann模型
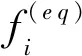
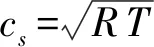


2.2 松弛时间及曲面滑移边界


2.3 局部Kn数

3 模型验证

4 微尺度气体渗流规律研究

4.1 不同Knm数下多孔介质内气体速度分布


4.2 不同Knm数下多孔介质渗流特性


5 结 论

