大气环境下的钢筋混凝土桥梁时变可靠度分析
陈水生, 赵 辉, 李锦华, 朱治蒸
(华东交通大学 土木建筑学院,南昌 330013)
1 引 言
近年来,随着我国高速公路交通量的增加,因车辆荷载作用而导致的桥梁垮塌事故时有发生,给桥梁管养单位和政府带来巨大的压力。特别是我国在役中小跨径的钢筋砼桥梁数量较多,在不同使用环境中运营的钢筋混凝土桥梁,其承载能力受混凝土碳化和钢筋锈蚀等不利因素的影响而逐年降低,桥梁的正常运营安全备受社会关注。
因此,学者们对在役钢筋混凝土桥梁的可靠度进行了大量的研究,Strauss等[1]研究了单片梁构件的可靠度问题;邓露等[2]分析了车辆轴限对钢筋混凝土简支T梁桥可靠度和加固费用的影响;孙晓燕等[3]评估了钢筋锈蚀对服役钢筋混凝土简支T梁桥耐久性的影响;金浩等[4]分析了钢筋混凝土简支T梁桥加固后的承载能力变化趋势,对加固后的可靠度进行了计算;乔牧等[5]分析了钢筋混凝土梁在火灾作用下的可靠度;李全旺等[6]考虑了荷载随机过程相关性对结构时变可靠度的影响;张强等[7]建立了考虑初始缺陷的混凝土结构锈胀时间预测模型,进而分析结构的可靠度;彭建新等[8]分析了钢筋混凝土简支T梁桥在氯盐环境下的随机失效概率;杨慧等[9]考虑混凝土碳化和氯离子累积效应的影响,对钢筋混凝土简支T梁桥后期服役阶段的可靠性进行了评估。
可以看出,上述学者对普通钢筋混凝土简支梁桥的可靠度研究取得了很多具有工程应用价值的成果,但这些研究也存在不足,(1) 对环境不利因素影响下的抗力退化,只考虑了单一因素的影响,而实际上抗力的退化是混凝土碳化、钢筋锈蚀及钢筋和混凝土黏结性能降低等不利因素的综合影响; (2) 车辆荷载视为平稳随机过程,而实际上各高速公路的交通量是逐年增加的,车辆荷载实为一非平稳随机过程。鉴于此,本文在已有研究的基础上,综合考虑多因素影响的桥梁抗力退化和车辆荷载的非平稳特征,分析普通钢筋混凝土简支梁桥在规范车辆荷载作用下的时变可靠度,为在役桥梁的建造和管养提供科学的指导和事前决策依据,研究意义重大。
2 大气环境作用的结构抗力概率模型
2.1 混凝土强度退化
结构的混凝土强度呈初期缓慢增长,后期逐渐下降的趋势,其过程是完全随机的且服从正态分布,其时变均值μfc d(t)和标准差σfc d(t)为[10,11]
(1)
式中μKM和σKM为材料强度的统计参数,fc d为混凝土强度设计值。
2.2 钢筋强度退化
一般大气环境条件下,锈蚀钢筋的屈服强度退化模型为[12]
(2)
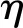
已有的研究结果表明,构件钢筋开始发生锈蚀的时间可以表示为[13]
tint=[(c-x0)/kc]2
(3)
式中c为混凝保护层厚度(mm),为随机变量,kc为构件混凝土碳化系数,x0为碳化残量。
而钢筋锈损率可以用钢筋锈蚀深度表示为[13]
(4)
式中d为钢筋直径,δe(t)为钢筋锈蚀深度(mm)。
进一步可得钢筋截面面积的时变值和钢筋截面面积的时变均值和时变标准差为
(5)
式中σAs(t)和μAs(t)分别为钢筋截面面积的标准差和均值,As 0为初始钢筋截面面积。
根据结构混凝土中钢筋锈胀破坏过程,通常将钢筋脱钝锈蚀引起的混凝土保护层锈胀开裂分为混凝土保护层锈胀开裂前和混凝土保护层锈胀开裂后两个时间段考虑。混凝土锈胀开裂前的钢筋锈蚀深度为[13]
δe 1(t)=λe 1(t-tint)
(6)
式中δe 1(t)为锈胀开裂前的钢筋锈蚀深度(mm),λe 1为锈胀开裂前的钢筋锈蚀速度(mm/a),其表达式为
(7)
式中kc r为构件的钢筋位置修正系数,角部取1.6,中部取1.0;kc e为构件所处环境修正系数,室外潮湿环境取值3.0~4.0,室外干燥环境取值2.5~3.5;fc u为混凝土立方体抗压强度,是随机变量。
当混凝土锈胀开裂后,此时的钢筋锈蚀速度会加快,其锈蚀深度计算公式为[13]
(8)
式中δc r为混凝土锈胀开裂时刻的锈蚀深度(mm),对于变形钢筋,其表达式为
(9)
式中kc r s为构件的钢筋位置影响系数,角部取1.0,非角部取1.35。
2.3 钢筋与混凝土黏结性能退化
(10)
综合考虑混凝土强度退化、钢筋强度退化及钢筋与混凝土黏结性能降低的多因素影响,基于式(1,2,10)的时变表达式,以受压区高度在翼缘板内的T型梁为例,可得锈蚀钢筋混凝土T型梁的抗力计算模型为
(11)
式中h0和b为T型梁的有效高度和截面宽度。
根据误差传递公式,可以推导出T型梁的正截面抗弯承载力均值和标准差为
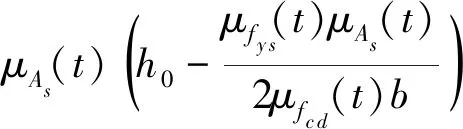
(12)
(13)
式中 变量ks(t),As(t),fy s(t)和fc d(t)各自独立,μ为其下标变量的均值,σ为其下标变量的标准差。
根据已有的研究,构件抗力不拒绝对数正态分布,其概率密度函数为[14]
(14)
3 荷载效应概率模型
3.1 永久荷载效应
桥梁结构的永久荷载即是桥梁结构的自重,在客观上是确定的,虽然其在结构服役时间内的变化较小,但综合考虑各因素的影响,可以认为结构永久荷载及其作用效应服从正态分布[3],永久荷载效应的概率密度函数为[2]
(15)
式中SGk为永久荷载效应标准值,μSG为永久荷载效应的均值。
3.2 车辆荷载效应
公路桥梁受到的可变荷载很多,其中最主要的可变荷载是车辆荷载。根据李扬海等[11]对不同桥梁类型和不同跨径桥梁的车辆荷载效应统计结果,桥梁在一般行车荷载(相当于现行规范的公路-II级)作用下的荷载效应截口分布服从威布尔分布,桥梁在密集行车荷载(相当于现行规范的公路-I级)作用下的荷载效应截口分布服从正态分布。桥梁的总车辆荷载效应由一般行车的车辆荷载效应和密集行车的车辆荷载效应组成。对于桥梁在未来服役期内的车流量增长这一非平稳车辆荷载,其直接结果就是密集行车所占的比重增加。那么,可得桥梁弯矩最大值的截口概率密度函数为
而平模机器的优点在于耗能小,机动性大,适合农村居民小规模应用,不适合工厂企业的大规模运作。其缺点在产量低,压力小,成型质量差。其工作面如加宽后,压辊和平模的磨损又不均衡,达不到更大的产量,配件拆装繁琐、维护麻烦。
(16)
式中MQk y和MQk m分别为一般行车和密集行车的弯矩标准值,p为密集行车所占的比重。
4 工程案例
以江西境内的某钢筋混凝土简支T梁桥为工程背景,该桥跨径20 m,桥梁上部结构由6片T梁组成,混凝土强度等级为C30,桥面铺装采用10 cm厚沥青混凝土+10 cm厚C25混凝土,桥梁横断面如图1所示。

图1 桥梁横断面(单位:cm)Fig.1 Cross section of bridge (unit:cm)
4.1 永久荷载效应计算
根据桥梁的设计图纸,采用Midas/Civil计算一期恒载和二期恒载的跨中弯矩标准值,因为桥梁为对称结构,表1只给出了1#,2#和3#T型主梁恒载效应的统计参数。

表1 恒载引起的跨中弯矩Tab.1 Midspan moment caused by dead load
4.2 车辆荷载效应计算
根据我国《公路桥涵设计通用规范》规定的桥梁结构整体计算方法,考虑冲击系数的影响,计算公路-I级车道荷载和公路-II级车道荷载的各片T型主梁跨中弯矩的统计参数,列入表2。
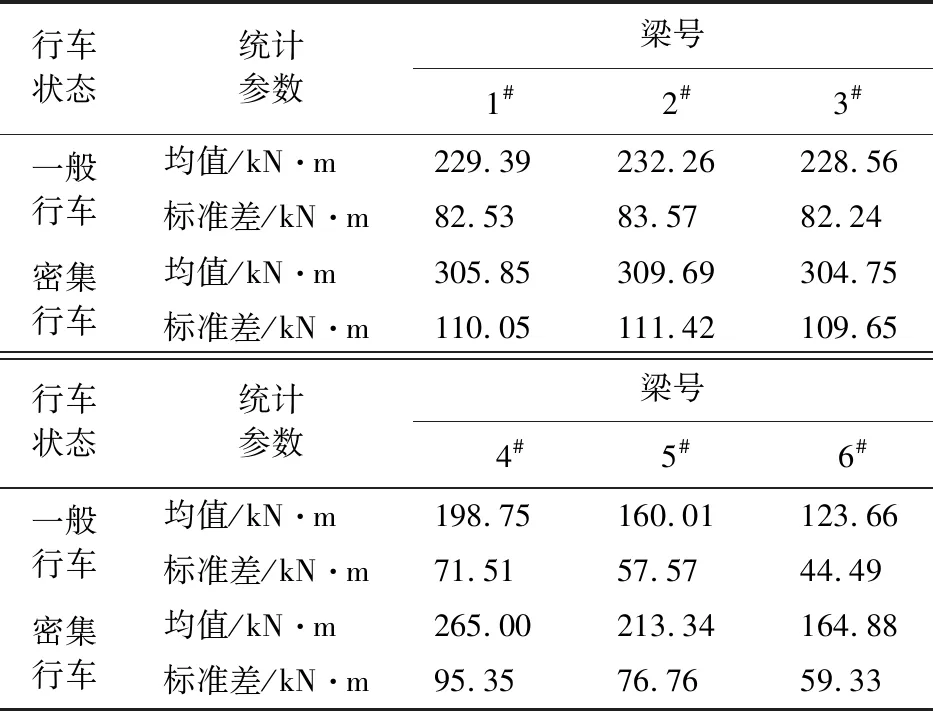
表2 车辆荷载引起的跨中弯矩Tab.2 Midspan moment caused by vehicle load
4.3 抗力计算
根据江西省气象资料,该桥地理位置的年平均湿度为77%,平均温度18 ℃。设计图纸的钢筋混凝土保护层最小厚度为30 mm,结合文献[11]可知,混凝土保护层厚度服从正态分布,其均值为 30 mm,标准差为1.488 mm。考虑混凝土强度的退化时变特性,由式(1)可得混凝土强度退化的时变概率密度函数及其脊线如图2所示,可以看出,在桥梁使用初期(前6年),混凝土强度增大,但随着桥梁服役时间的延长,混凝土强度逐渐衰减,混凝土强度均值从第6年的27.82 MPa衰减到第100年的22.62 MPa。可见,即使是一般大气环境,桥梁结构的混凝土强度也会随着服役期的增加而减小。
从式(3)可以看出,钢筋锈蚀开始时间是随机变量,采用传统Monte Carlo随机抽样的方法,经统计分析可知钢筋锈蚀开始时间不拒绝对数正态分布。图3给出了主梁角部钢筋强度退化的时变概率密度函数及其脊线,可以看出,钢筋强度在桥梁服役的前6年没有退化,但从第7年开始,钢筋强度逐渐衰减,从第7年的273.3 MPa衰减到第100年的257.7 MPa,衰减幅度为15.6 MPa。
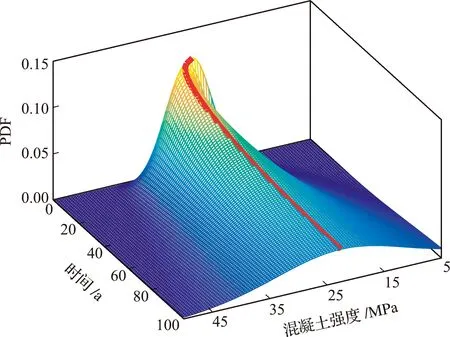
图2 混凝土强度退化的时变概率密度函数Fig.2 Time varying probability density function diagram of strength degradation of concrete

图3 钢筋强度退化的时变概率密度函数Fig.3 Time varying probability density function diagram of steel strength degradation
根据式(10),图4给出了主梁钢筋与混凝土协同工作系数的时变均值,可以看出,钢筋与混凝土的协同工作系数随着桥梁服役时间的增加而减小,角部钢筋与混凝土的协同工作系数在服役16年后下降,而非角部钢筋与混凝土的协同工作系数在服役27年后下降,且下降幅度小于角部钢筋。
根据我国《公路钢筋混凝土及预应力混凝土桥涵设计规范》的计算方法,本文T型主梁正截面的抗弯承载力按宽度为1.58 m的矩形截面来计算。为对比分析一般大气环境作用的混凝土强度退化、钢筋强度退化及钢筋与混凝土黏结性能降低对T型主梁抗力的影响,在此讨论四种抗力退化模型。模型一,钢筋与混凝土的黏结性能不降低;模型二,混凝土强度不退化;模型三,钢筋强度不退化;模型四,同时考虑混凝土强度退化、钢筋强度退化及钢筋与混凝土黏结性能降低。根据式(11),采用Monte Carlo随机抽样的方法统计四种抗力退化模型的主梁正截面抗力分布参数,统计分析结果表明,主梁抗力不拒绝对数正态分布,模型四的主梁抗力时变概率密度函数及其脊线如图5所示,不同抗力退化模型的主梁抗力时变均值曲线如图6所示,可以看出, (1) 随着桥梁服役时间的延长,抗弯承载力的离散性减小; (2) 不同的抗力退化模型,T型主梁正截面抗弯承载力随着桥梁服役期的延长而减小; (3) 钢筋强度退化对抗弯承载力影响最大,其次是钢筋与混凝土的黏结性能降低,而混凝土强度退化对抗弯承载力的影响较小,抗弯承载力在第6年开始退化。由此可见,保证钢筋混凝土桥梁良好承载能力的关键是防止钢筋锈蚀及其引起的与混凝土黏结性能降低。
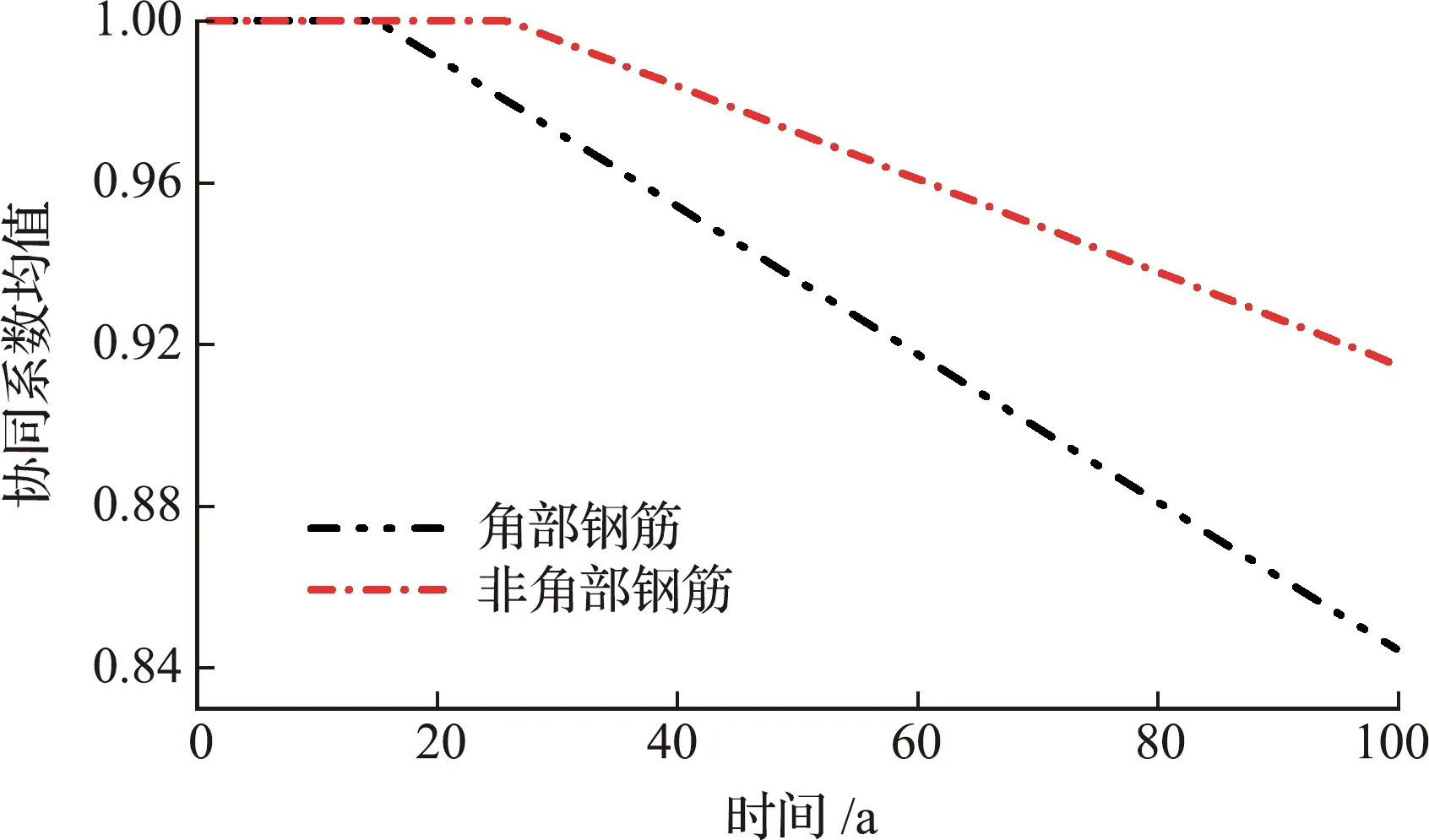
图4 钢筋与混凝土协同工作系数时变均值Fig.4 Time varying mean of cooperative work coefficient between steel and concrete
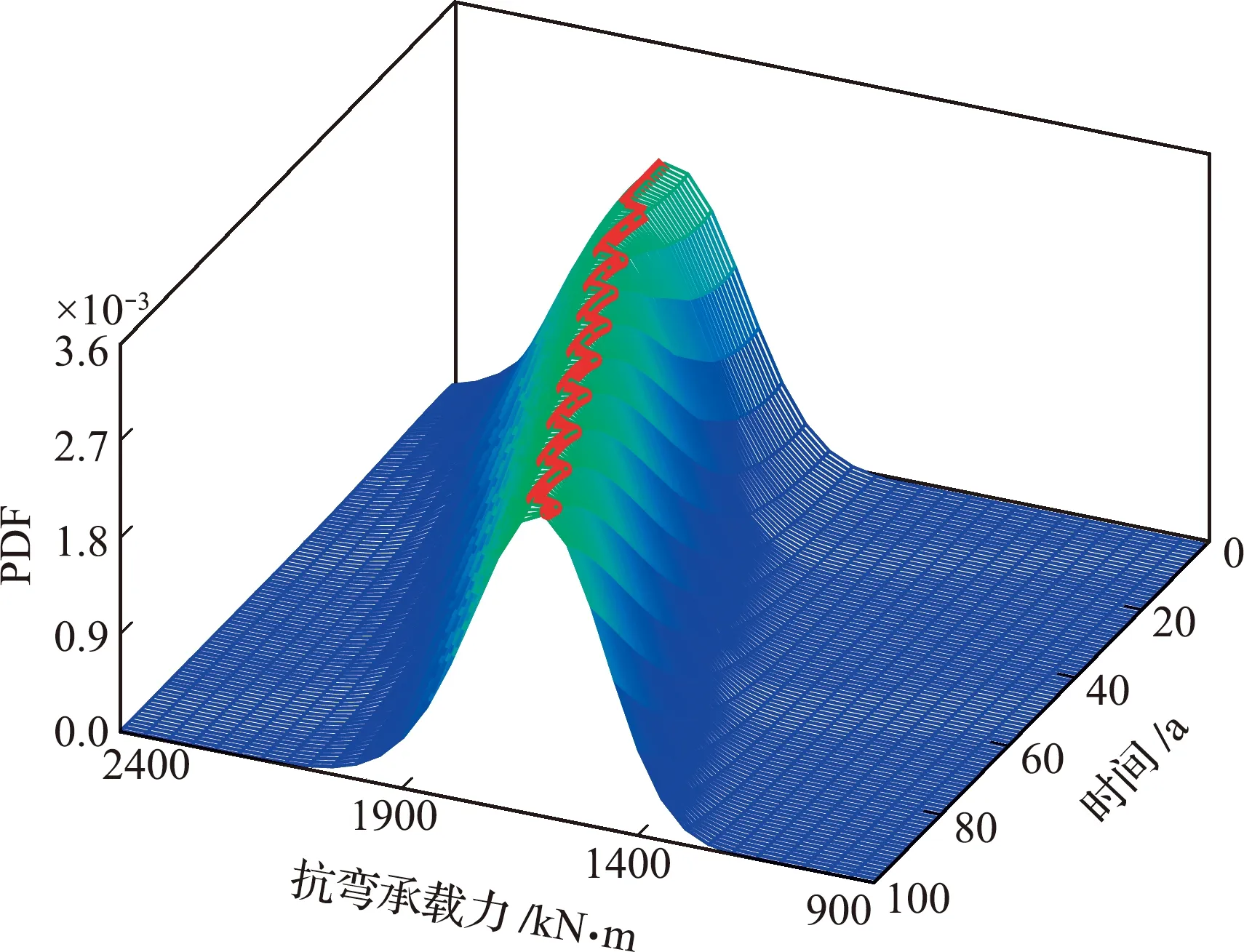
图5 模型四的抗力时变概率密度函数Fig.5 Time varying probability density function of resistance in model 4
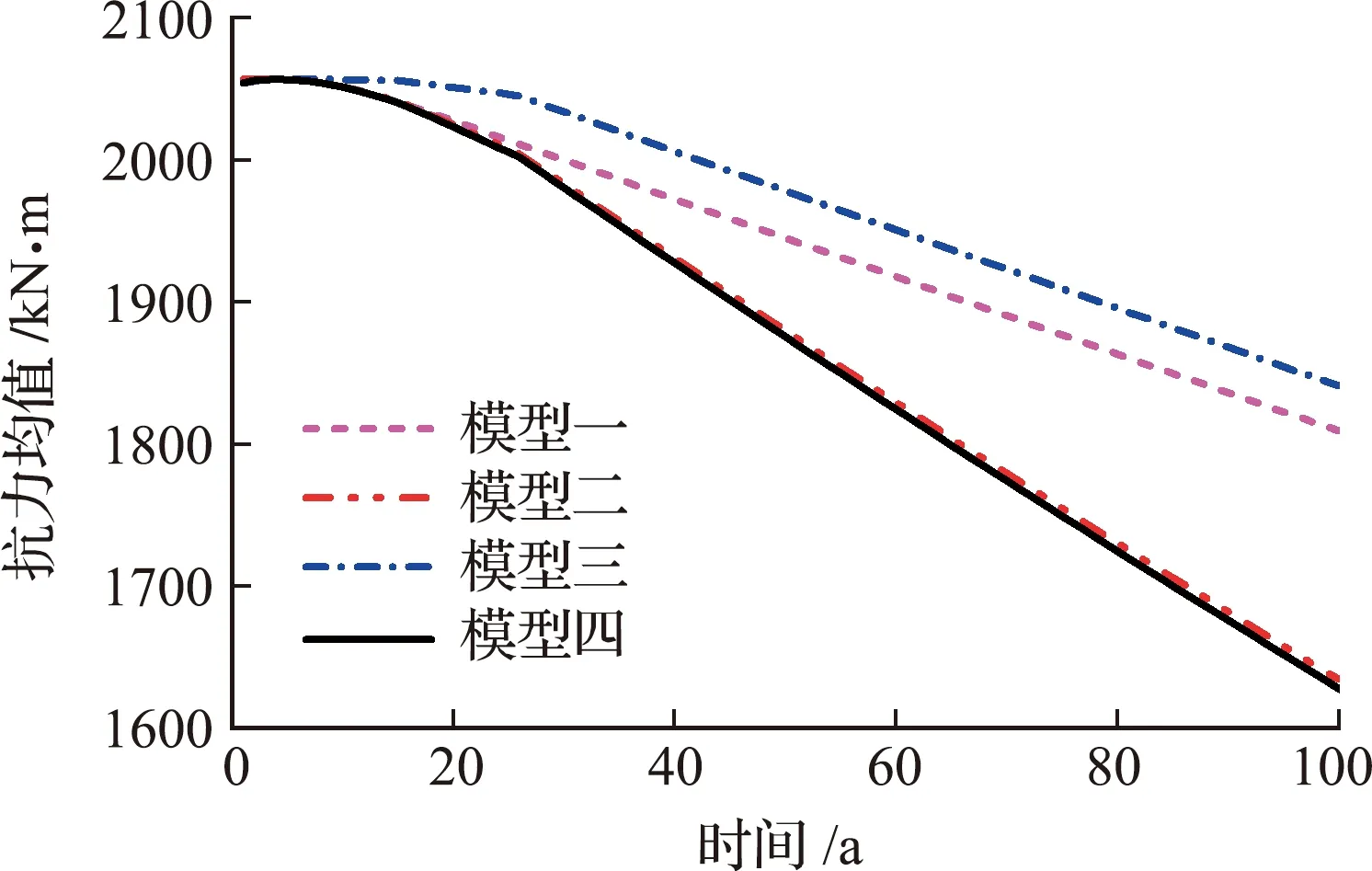
图6 不同退化模型的抗力时变均值Fig.6 Time varying mean resistance of different degradation models
4.4 时变可靠度计算
本文在计算桥梁的时变可靠度时,时段长度为一年,构件失效概率为不同时段的失效概率,计算方法参见文献[15]。6片T型主梁构成一个串联系统,任何一片主梁失效,就意味着整个桥梁系统不能继续正常运营。设Pf i为第i片梁的抗弯失效概率,则整个桥梁体系的失效概率为
(17)
采用多因素影响的抗力退化模型四,取密集行车占比为0.15,当车辆荷载为平稳随机过程时,图7 给出了各片T型主梁的时变可靠指标,可以看出,各片T型主梁的可靠指标随着桥梁服役期的延长而减小;1#梁和2#梁的抗弯可靠度较小,第100年的可靠指标为4.63,而6#梁的抗弯可靠指标最大,其失效的概率较小;直接承受车辆荷载作用的T型主梁,其可靠指标小于非直接承受车辆荷载作用的T型主梁。
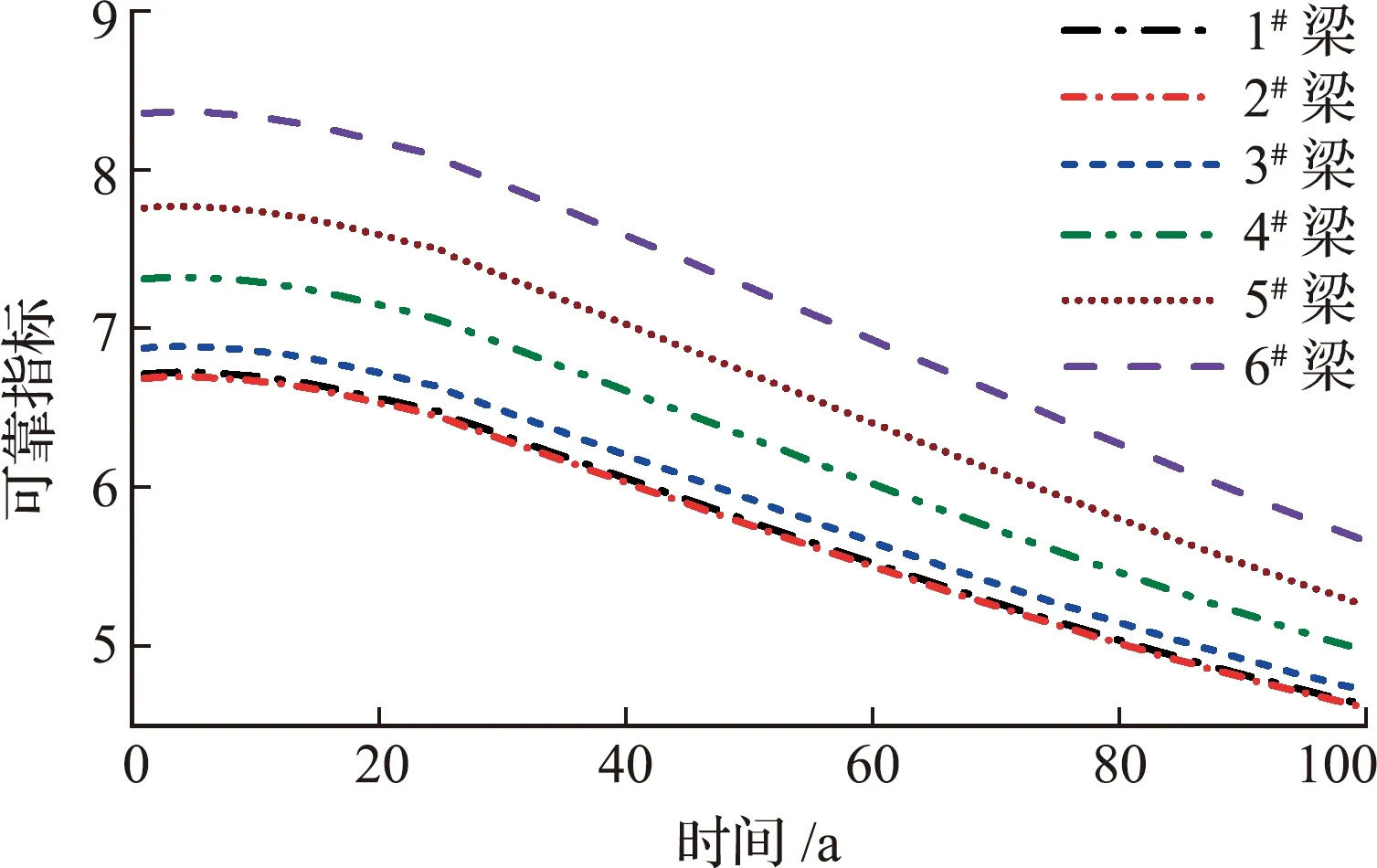
图7 各片T型主梁的时变可靠指标Fig.7 Time dependent reliability of each T-shaped girder
不考虑交通量的逐年增长,在密集行车占比分别为0.15,0.25和0.35的情况下,整个桥梁系统的时变可靠度如图8所示,可以看出,整个桥梁系统的可靠指标随着桥梁服役时间的延长而减小,密集行车占比越高,桥梁可靠指标下降就越多;如果将桥梁的目标可靠指标设为β=4.2[16],在桥梁设计基准期内,密集行车占比小于0.35时,桥梁是安全的,密集行车占比大于0.35时,桥梁在服役期内的失效概率会随着密集行车占比的提高而增大。
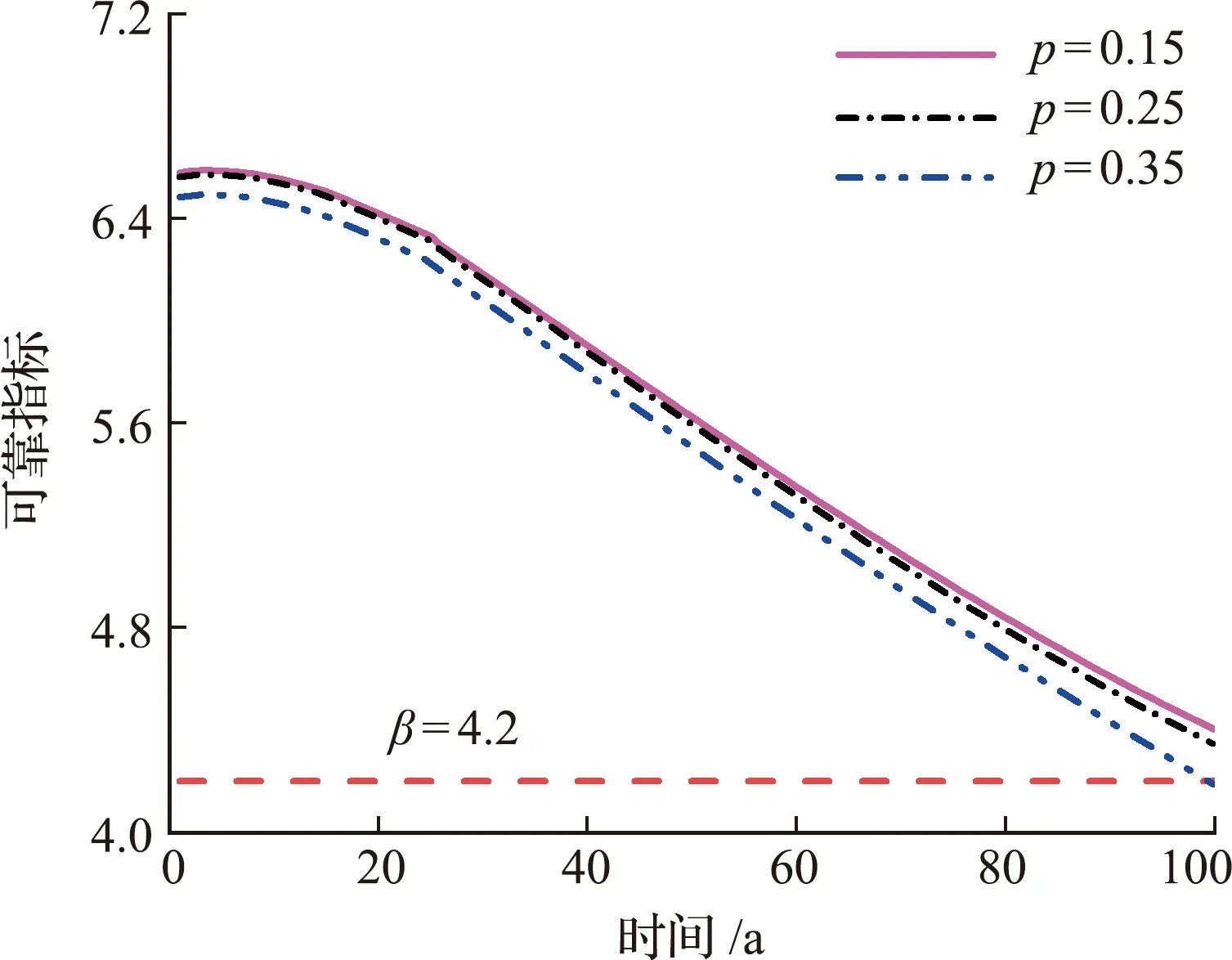
图8 不同密集行车占比的桥梁时变可靠指标Fig.8 Time dependent reliability of bridge with different proportion of intensive traffic
而实际的交通量是时变的,特别是我国经济的快速增长和跨区域货运的增多,公路桥梁的过桥车辆每年都在增加,即车辆荷载在桥梁的服役期内为非平稳随机过程。为对比非平稳车辆荷载对桥梁时变可靠度的影响,在密集行车初始占比0.15的基础上,当密集行车占比以0.005的增量值逐年增加时,桥梁在平稳和非平稳车辆荷载作用下的时变可靠指标如图9所示,可以看出,非平稳车载作用的桥梁可靠指标小于平稳车载的桥梁可靠指标,交通量的增加使桥梁失效的概率增大且在服役到第83年时就需要加固维修。

图9 非平稳车载的桥梁时变可靠指标Fig.9 Time varying reliability index of bridge with non-stationary vehicle load
当密集行车占比分别以0.005,0.006和0.007的增量值逐年增加时,图10给出了不同交通量增量值的桥梁时变可靠度,可以看出,交通量增量值越大,桥梁可靠度下降越快,桥梁承载能力失效的时间相应提前,分别为第83年、第78年和第73年;可见,在未来服役期内,随着交通量的大幅增长,桥梁失效的概率增大。

图10 交通量增长的桥梁时变可靠指标Fig.10 Time varying reliability index of bridges with increasing traffic volume
5 结 论
在一般大气环境下,随着桥梁服役时间的延长,钢筋混凝土桥梁的混凝土强度会逐渐衰退,当混凝土碳化到钢筋表面时,钢筋强度会因锈蚀而降低,且混凝土与钢筋间的黏结性能下降。综合考虑混凝土强度退化、钢筋强度退化及钢筋与混凝土黏结性能降低的多因素影响,桥梁抗力随着桥梁服役时间的增加而明显减小,其中钢筋发生锈蚀而导致的强度降低是普通钢筋混凝土桥梁抗力减小的主要因素,而混凝土强度退化对抗力的影响较小。桥梁可靠指标随着桥梁服役时间的增加而减小,当密集行车占比提高时,桥梁失效的概率增大且失效时间提前。考虑交通量的逐年增加,桥梁的可靠指标迅速降低,维修加固时间提前。

