模拟相变问题的精细积分边界元法

姚鸿骁, 左 冲, 胡小飞, 姚伟岸*

(1.大连理工大学 工业装备结构分析国家重点实验室，大连 116024； 2.三一重工集团有限公司，武汉 430100)

1 引 言

相变传热问题常见于多种工程实际问题中，如金属铸造、焊接、晶体生长、食品冷冻和相变储能系统[1]等。因为相变过程中存在随时间变化的相变界面以及潜热的吸收或者释放，因此相变问题属于非线性问题。只有少数一维或半无限问题可以获得解析解，相变问题主要依靠数值方法求解。

处理移动界面和潜热变化的方法主要有固定域法和界面追踪法两种。固定域法将模拟区域视作一个整体，基于热焓、等效热容或者热源项建立统一的传热控制微分方程，并通过温度场的插值确定相变界面的位置[2,3]。但由于相变温度附近参数存在不连续性甚至阶跃，其非线性方程的模拟存在收敛性问题，尤其是相变潜热数值较大时。界面追踪法则不需要处理这种不连续性，而是分别在固相和液相两个区域中求解瞬态传热问题，然后根据相变界面上的能量连续条件追踪界面的移动[4]，但界面追踪法需要连续地对离散网格进行重划分。

空间离散的数值方法主要有有限元法、有限差分法、有限体积法、无网格法和边界元法。其中边界元法已经成为求解传热问题的有效方法之一，如周枫林等[5]使用边界元法分析了混凝土水坝的瞬态热传导问题；高效伟等[6]提出了一种三维等参管单元边界元法，并将其应用于热传导分析中；赵金军等[7]提出了一种计算几乎奇异边界积分的边界元方法并求解了三维非均质热传导问题。相对其他方法,边界元法的主要优点是只需离散求解域的边界。因此，边界元法非常适合于求解移动边界问题和边界未知的反问题，如左冲等[8]利用时域径向积分边界元法和界面追踪法模拟了平面单相凝固问题；Wang等[9]将边界元法与水平集法相结合模拟了具有复杂拓扑变化的相变问题；Yu等[10]提出了一种基于边界元法的直接反演方法来辨识内部空腔的形状。

本文采用精细积分边界元法和界面追踪法求解两相等温相变问题。首先，分别在固液两相中利用位势问题的基本解建立积分方程，并采用径向积分法[11]将其中的域积分转化为边界积分。然后，利用边界元法和精细积分法[12]分别求得固液两相的温度场和边界热流密度。最后，基于相变界面上的能量平衡方程,采用界面追踪法得到移动界面的位置。

2 控制方程

如图1所示的二维相变问题，相变界面Γif将整个区域Ωtotal分为固相Ωs和液相Ωl两个区域。如忽略密度变化，则传热控制微分方程为

(x∈Ωs)(1)

(x∈Ωl)(2)

式中x=(x1,x2)，=∂/∂x1i+∂/∂x2j,T(x,t)为t时刻点x的温度，c,k和分别为比热容、热导率和密度，f(x,t)为域内热源。

图1 相变问题Fig.1 Phase change problem

边界条件为

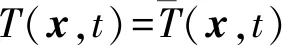
(x∈Γ1)

(3)

(x∈Γ2)

(4)

式中n为单位外法向量，q为热流密度。

初始条件为

T(x,0)=T0(x)

(t=0)

(5)

相变界面Γif的温度条件和能量平衡条件

T(x,t)=Tm

(x∈Γif)

(6)

(x∈Γif)

(7)

式中Tm为相变温度，L为相变潜热，Vn为相变界面的法向移动速度，其由固液两相的热流得到。

分别在固相域和液相域中应用径向积分边界元法求解，省略下标s和l，固液两相的控制方程可统一写为

(8)

3 精细积分边界元法

基于式(8)的积分方程为

(9)

(10)

式中r(x,y)为源点y到场点x的距离。

需要利用径向积分法[11]将式(9)的域积分转化为边界积分，其中∂T(x,t)/∂t为未知量，可用径向基函数和坐标分量的多项式将其近似表示为

(11)

(12)

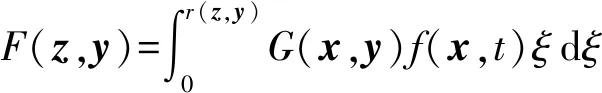
(13)

式中Dy为N维横向量，其第j个分量为

(14)

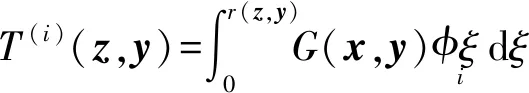
(15)

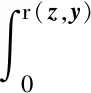
(16)

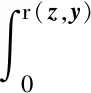
(17)

将边界Γ离散为Ne个边界单元和Nb个边界点，域内配置Ni个内部点，N=Nb+Ni。源点y取遍所有边界点和内部点，由式(12)得出式(18)，即

(18)

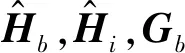
(19)

然后，利用精细积分法[12]求解式(19)，如果r在时间步[tk,tk + 1]内是关于时间的线性函数，则式(19)的求解如下。

Xk + 1=E[Xk+B-1r0+r1]-

B-1(r0+Δtr1)-r1

(20)

式中 Δt=tk + 1-tk，E=exp(BΔt)

r0=r(tk)，r1=[r(tk + 1)-r0]/Δt

4 界面追踪法

为了追踪相变界面的移动位置，界面追踪法首先需要确定界面的移动速度和方向。界面移动速度由式(7)计算得到，而界面移动方向由式(21)计算[14]

(21)

式中 下标j为移动界面上的j号节点，下标i-1和i为j号节点相邻的两个单元，l为单元长度。

时间步[tk,tk + 1]内界面追踪法的步骤如下。

(1) 指定一个界面最大移动距离Δs。

(2) 根据初始条件或者上一时间步数值结果得到tk时刻固相域和液相域的边界热流qs(tk)和ql(tk)，跟据式(7)计算速度V(tk)={Vj(tk)}。

(3) 利用式(22)计算时间步长[15]

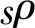
(22)

式中 ‖·‖∞为向量的无穷范数。

(4) 预测tk + 1时刻的界面移动速度为Vp(tk + 1)= 0.7V(tk)。

(5) 利用式(23)计算移动界面上节点预测位置

(23)

(6) 更新tk + 1时刻的网格，在固相域和液相域分别利用精细积分边界元法求解未知温度场和热流密度qs(tk + 1)和ql(tk + 1)，再依据式(7)计算速度V(tk + 1)={Vj(tk + 1)}。

(7) 收敛性检测，如收敛条件满足

(24)

则进入步骤(8)，否则令Vp(tk + 1)=V(tk + 1)，回到步骤(5)。

(8) 步骤(5)得到的移动界面位置和步骤(6)得到的温度场即为tk + 1时刻的计算结果，对移动界面进行网格重划分，并根据需要增加或者删减内部节点。令tk=tk + 1，回到步骤(1)。

5 数值算例

利用四个数值算例来验证本文提出的数值方法。数值计算通过Matlab编程实现，界面追踪法终止迭代的容许差限统一为ε=0.001。

算例1考虑一个一维半无限凝固相变问题。初始温度为T0=2 ℃，x1=0处边界的温度保持为Tw=-10 ℃，其他边界保持绝热。相变材料的热物理参数列入表1。该问题可用图2所示的二维1×0.1(m2)矩形区域的相变问题近似。

表1 相变材料热物理参数Tab.1 Thermo -physical properties of the phase change materials

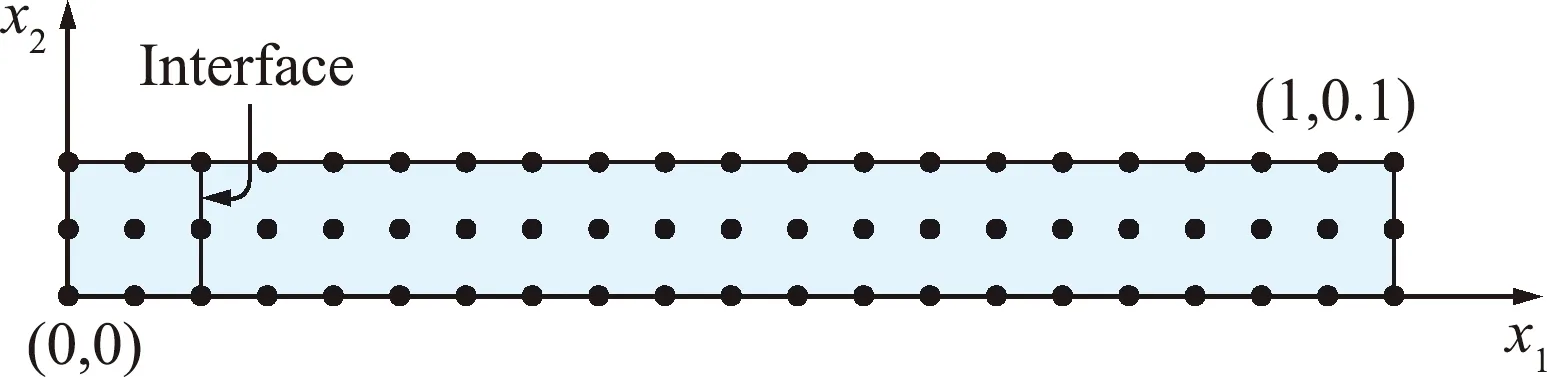
图2 算例1的边界元计算模型Fig.2 BEM model for Example 1

在计算过程中，相变界面每移动0.02 m,则在固相域增加2个边界节点和3个内部节点，相应在液相域减少2个边界节点和3个内部节点。图3给出了不同时刻相变界面位置与解析解[16]对比的相对误差，吻合良好。可以看出，Δs分别取0.004 m，0.006 m和0.008 m时,最大误差分别是0.63%，0.89%和1.15%，计算结果均具有很高精度。

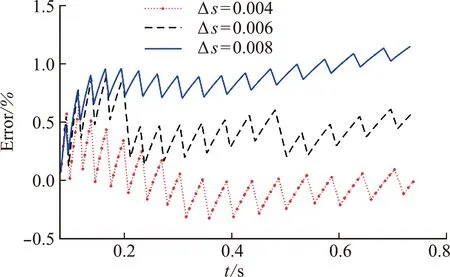
图3 算例1的界面位置相对误差Fig.3 Relative errors of interface position for Example 1

算例2考虑一个无限角域凝固问题。初始温度为T0=0.3 ℃，x1=0和x2=0处边界的温度保持为Tw=-1 ℃，其他边界保持绝热。相变材料的热物理参数列入表1。该问题可用图4所示的一个二维1×1(m2)正方形区域的凝固相变问题来近似。

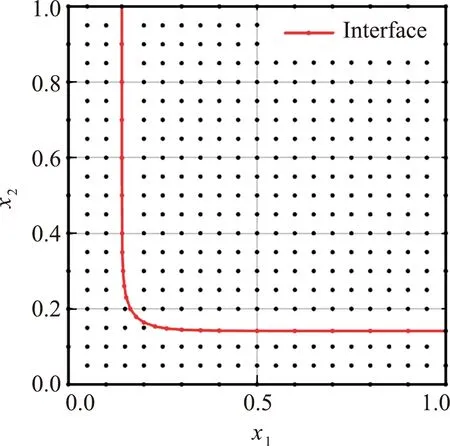
图4 算例2的边界元计算模型Fig.4 BEM model for Example 2

表2列出了Δs=0.02 m时，采用本文方法模拟得到的不同时刻相变界面与x1=1和x1=x2两条直线交点的x2坐标值以及对应的解析解[17]，其中括号内为相对误差，最大相对误差分别为 0.96% 和0.44%。虽然界面追踪法需要迭代求解相变界面的位置，但本文方法能够快速收敛得到结果，如对算例2，每个时间步的平均迭代次数为2.9，最大次数为4。

表2 算例2相变界面位置与误差Tab.2 Interface positions and relative errors for Example 2

虽然铜管域内不发生相变，但需对铜管进行瞬态热传导问题数值分析。分别在铜管域和相邻的相变材料域应用边界元法，得到两组微分方程。基于铜管-相变材料界面上的温度连续条件和热流平衡条件，这两组微分方程可联立形成一组新微分方程组。利用精细积分法求解得到温度场和边界热流。

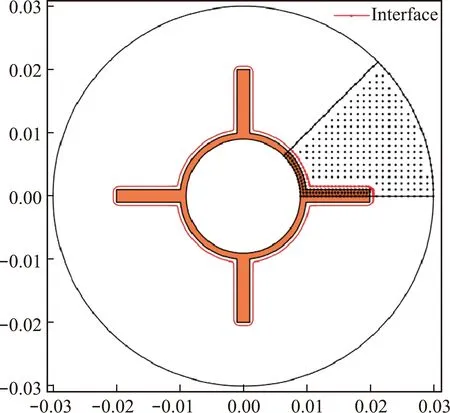
图5 算例3的边界元计算模型Fig.5 BEM model for Example 3

基于对称性，选取装置截面的1/8进行数值计算。图6给出了不同时刻相变界面的移动位置，同时图7给出了固相分数的变化。以ANSYS软件的数值模拟结果作为参考解，对比结果表明,本方法具有很高的模拟精度。

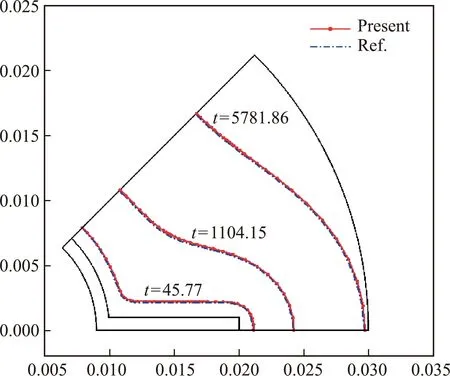
图6 算例3的相变界面位置Fig.6 Phase change interface position for Example 3

图7 算例3的固相分数变化Fig.7 Evolution of solid fraction for Example 3

算例4考虑如图8所示区域的相变问题。初始温度为T0=-10 ℃，外边界的温度保持为Tw=25 ℃。相变材料的热物理参数列入表1。

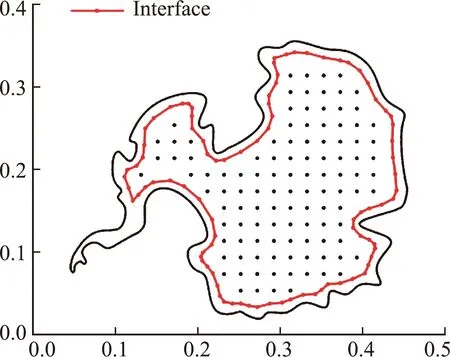
图8 算例4的边界元计算模型Fig.8 BEM model for Example 4

图9给出了不同时刻相变界面的移动位置，并与ANSYS软件数值结果进行了对比。可以看出相变区域发生了拓扑变化，但本文方法仍然能够有效且精确地模拟此类相变问题。

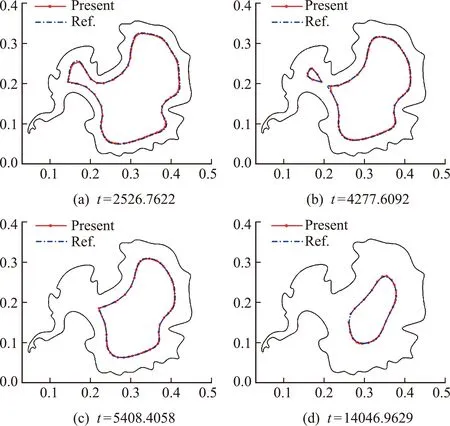
图9 算例4的相变界面位置Fig.9 Phase change interface position for Example 4

6 结 论

本文将精细积分边界元法与界面追踪法相结合求解二维双相相变问题。数值算例的结果表明，本文提出的方法能够有效地模拟相变问题，并且具有精度高和迭代次数少的优点。对于相变区域发生拓扑变化的问题本文方法仍然是有效的，能够得到精确的模拟结果。当相变界面最大移动距离Δs取不同数值时，本文方法依然能够得到稳定的数值解，表明本文方法具有很好的数值稳定性。