变截面悬链线无铰拱应变影响线的解析解
周 宇, 许成超, 赵 青, 王雪忠
(1.安徽建筑大学 土木工程学院,合肥 230601; 2.安徽省BIM工程中心,合肥 230601)
1 引 言
悬链线拱轴线型作为一类典型的曲线族[1,2],在中小跨径实腹式无铰拱和大跨空腹式无铰拱中有着广泛的应用[3-7],为实现更合理的受载,工程中多采用变截面拱结构作为板拱桥和系杆拱桥的拱肋截面进行设计[8]。影响线作为桥梁结构的固有静力特征,可以全面反映其截面刚度特性,是桥梁结构设计的重要参数,且近年在桥梁损伤计算领域也逐渐成为热点[9-12],其应用前景广阔[10,11]。但由于超静定拱桥结构影响线的求解过程复杂,仍未见变截面悬链线无铰拱应变影响线解析解研究的相关报道。

基于Ritter截面变化公式简化悬链线曲线积分,结合弹性中心[15]简化体系下的力法方程,推导了变截面悬链线无铰拱应变影响线的显式解,针对拱轴力随矢跨比变化的特性展开研究,并通过四座不同矢跨比下的悬链线无铰拱结构多个截面的有限元解校验了相关结论,研究结果可用于工程计算与模型分析借鉴。
2 应变影响线解析解
2.1 计算思路
变截面抛物线无铰拱的基本结构如图1所示。
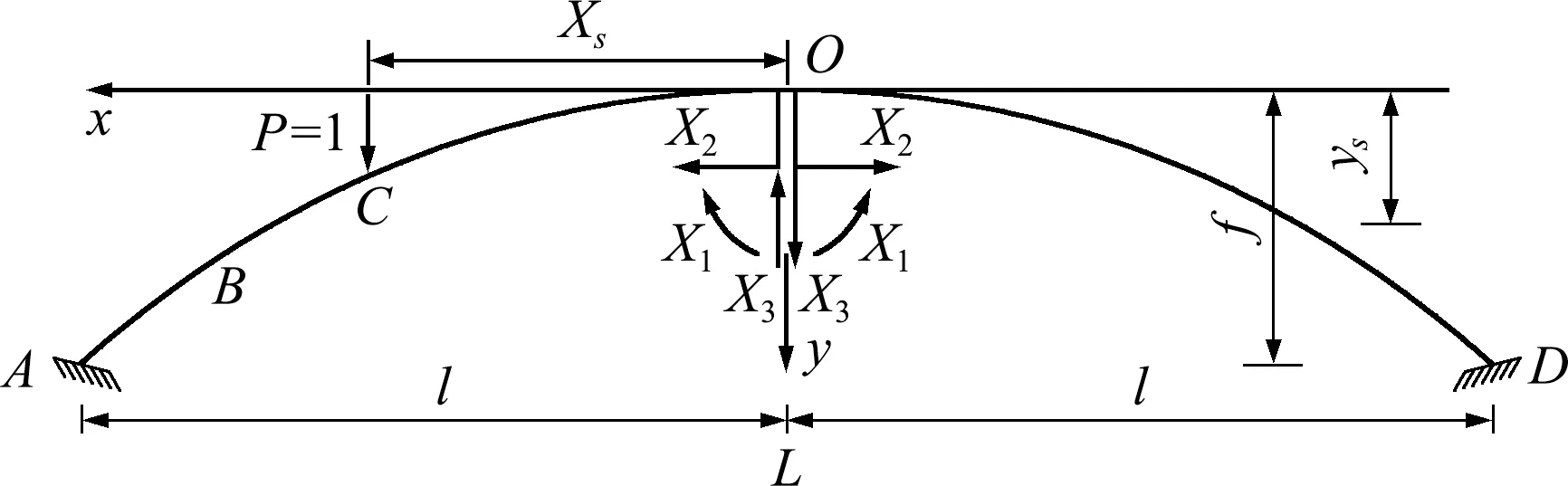
图1 拱轴基本体系Fig.1 Arch shaft basic system
拱轴几何量表达式与悬链线拱轴方程为
y=f(chkx/l-1)/(m-1)
(1)
(2)
式中f为拱肋矢高,m为拱轴系数,l为拱轴半跨径。截面按Ritter公式设置拱轴曲线,

(3)

(4)

(5)
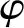
利用力法将无铰拱分成左右对称的悬臂拱,如图1所示,跨中冗力为x1,x2和x3;采用弹性中心法简化力法方程,设点C移动力坐标为xS。
2.2 冗力及其影响线计算
冗力影响线求解是求解应变影响线的基础,冗力作用下截面内力及影响线列入表1和表2。

表1 冗力作用下结构基本内力Tab.1 Internal forces under the effect of redundant forces

表2 冗力影响线计算Tab.2 Redundancy impact line calculations
2.3 应变影响线的计算
根据图2,对O处的冗力和C处的移动力在截面B处的作用列平衡方程,求截面B的应变影响线,
εB=εM B+εN B=MB/WZ· BE+NB/EAB
(6)

(7,8)
式中εB为B截面应变,MB为B截面弯矩,WZ·B为B截面抗弯截面系数,E为拱肋材料弹性模量,NB为B截面轴力,AB为B截面面积,b为拱截面宽(等宽变高截面),hB为B截面高度。

图2 B截面内力Fig.2 Section B internal force
根据移动力位置,MB和NB可分以下情况,
(9)
(10)
根据式(6~8),得截面B处应变影响线,
式中x1,x2和x3的展开形式已列入表2,因篇幅限制,不再赘述。
3 算例分析
为验证应变影响线的解析准确性,以四个变截面悬链线无铰拱为例,通过MIDAS/Civil建立有限元模型,对比推导的应变影响线计算结果,并比较解析解与有限元解的相对误差。四座拱跨径均为50.934 m,矢跨比分别为1/2,1/3,1/5和1/7, 如图3所示,拱肋截面宽1 m,跨中拱截面高1.1 m,截面高按Ritter公式变化,材料弹性模量为3.45E+07 kN/m2,拱轴系数m为1.988,拱厚变化系数n为0.4,本文公式解析和有限元计算的l/2和l/4截面应变影响线如图4和图5所示,典型截面数值结果列入表3。

图3 四种矢跨比拱轴线Fig.3 Four kinds of sagittal span ratio arch axes
由表3及图4和图5表明,对不同矢跨比的拱轴,当考虑轴力时,算例中四种变截面悬链线无铰拱应变影响线的解析解与有限元计算结果偏差均小于2%。然而在未考虑轴力时,1/2和1/3矢跨比的变截面悬链线无铰拱应变影响线解析解的计算偏差尚能控制在2%以内,但1/5和1/7矢跨比的l/2测点应变影响线解析计算偏差较大,在2%以上,且最大计算偏差大于9%。针对同一矢跨比,l/4测点比l/2测点处的影响线解析偏差普遍较小,同时l/4测点较l/2测点受轴力的影响更小,在未考虑轴力时的计算偏差也均能控制在2%以内。

表3 算例典型截面数值对比表Tab.3 A values comparison of cases in typical sections

图4 本文公式法与有限元法计算结果对比(算例1)Fig.4 Comparison of the calculation results between formula method and finite element method (Example 1)
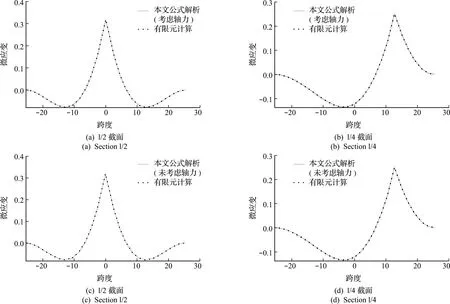
图5 本文公式法与有限元法计算结果对比(算例4)Fig.5 Comparison of the calculation results between formula method and finite element method (Example 4)
4 结 论
(1) 在变截面遵循Ritter公式规律的基础上,推导得到变截面悬链线无铰拱应变影响线解析解。本文公式解析与有限元计算结果最大偏差小于2%,符合工程精度要求,可作为任意拱轴系数及矢跨比下悬链线变截面无铰拱应变影响线计算依据。
(2) 研究同一拱轴系数下不同矢跨比的变截面悬链线无铰拱应变影响线,对是否考虑轴力的计算结果进行对比,发现随矢跨比愈小,轴力对结果的影响愈大,计算偏差也就越大,对于矢跨比1/7的坦拱,考虑轴力最大偏差小于2%,未考虑轴力的最大偏差大于9%。
(3) 同一矢跨比拱,测点位置不同,轴力影响程度也不同,l/4跨处轴力对其鲜有影响,l/2跨处轴力对其影响程度较大。
(4) 悬链线无铰拱的变截面并非都按Ritter规律变化,其他截面高度变化规律对悬链线无铰拱应变影响线的影响,有待进一步研究。
——以徐州高层小区为例

