基于梁连续抗弯刚度与小波变换的结构损伤识别方法研究
郭 佳, 管德清
(1.长沙理工大学 土木工程学院,长沙 410000; 2.湖南城市学院 土木工程学院,益阳 413000)
1 引 言
结构在使用过程中会出现各种难以预测的损伤,从而使得结构的物理特性逐渐减弱,当损伤累积到一定程度时,将导致结构丧失功能而发生倒塌。因此在实际中需要对结构进行损伤识别,确定损伤位置与损伤量,从而为结构的整体性能评估提供依据,而确定损伤位置是最基本和最重要的前提。
目前结构损伤位置识别的方法分为有损识别方法和无损识别方法,而在小损伤识别中,无损识别方法是目前最推荐使用的方法,其包括声发射(AE)[1]、超声扫描[2]、导波[3]和振动[4]等。基于振动的结构损伤识别方法已广泛用于结构损伤识别,其演化出的方法主要有基于结构动力特性的损伤识别方法[5,6]、基于小波变换的结构损伤识别方法[7,8]和基于智能算法的结构损伤识别方法[9,10]等。基于小波变换的结构损伤识别方法,不需要损伤区域无损信息就能从结构的模态形状中找到奇异点,从而能直观地显示结构损伤位置[11],因此基于小波奇异性检测结构模态形状的方法在识别结构损伤位置时具有很大优势[12,13]。但是小波系数存在边缘效应奇异性,使得边缘损伤识别会出现误判,从而导致结构的边界损伤难以识别[14]。在试验中,结构损伤对周边的影响导致小波系数模极大值难以精确识别损伤位置,因此在未知结构无损信息的情况下,仅基于损伤结构的小波系数奇异性难以精确定位损伤位置。
基于以上存在的问题,本文结合梁结构连续抗弯刚度与小波系数的特点,提出了识别实际结构边缘损伤位置并精确定位损伤位置的方法。
2 小波奇异性原理
设Ψ(t)是基本小波,对于f(t)∈L2(R),其连续小波变换(CWT)定义为
(1)
式中a≠0,b和t均为连续变量,Ψ*(t)为Ψ(t)的复共轭。

(2)
函数f在尺度因子s上对应的基本小波的连续小波变换为
(3)
式中s>0,式(3)说明,小波变换模极大值是经平滑后的一阶导数极大值,对应信号的奇异点。
3 损伤梁连续抗弯刚度的推导
如图1所示为一含t条贯通损伤的固支梁,以该梁为例来推导损伤梁连续抗弯刚度(简称刚度),从而可以通过梁连续抗弯刚度计算出损伤对周围的影响规律与影响范围。
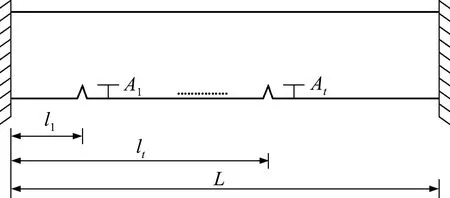
图1 含贯通损伤固支梁Fig.1 Fixed beam with transfixion damage
在恒定弯矩M的作用下,未开裂梁的应变能为
(4)
当梁出现t条裂纹后,裂纹i从0增长到Ai时,根据断裂力学,所有裂纹扩展消耗的能量为

(5)
式中B为梁高,Gi为应变能释放率,li为裂纹i所处位置。对于梁的横向振动而言,裂缝主要承受直接弯曲应力,剪切应力可以忽略。则应变能释放速率为
(6)
式中Kli为裂纹的应力强度因子,E为杨氏模量。对于实心矩形截面梁,Kli为[15]
(7)
式中h为梁高,当At/h<0.6时有
F(Ai)=1.12-1.4(Ai/h)+7.33(Ai/h)2-
13.8(Ai/h)3+14(Ai/h)4
(8)
因此,可以得到裂纹产生需消耗的能量为
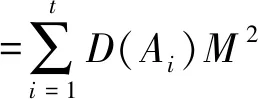
(9)
式中
(10)
假定EIli为裂纹i始终张开的裂纹梁抗弯刚度,则其开裂的最终应变能可替换表示为
(11)
式中Ili为裂纹i处梁的截面惯性矩,E为弹性模量。
根据断裂力学,应力/应变高度集中在裂纹尖端附近,并在远离裂纹的位置达到名义应力。因此,可以假定在恒载的作用下,裂纹扩展引起的应变能增加主要集中在裂纹区域附近。为了从数学上表示应变能沿裂纹梁长度的变化,Eli可表示为[16]
(12)
式中li为裂纹i的坐标,在裂纹处可以取最大值,在远离裂纹处趋近于0,Q(Ai,li)与k(Ai)为待定函数。
由于应变能主要集中在裂纹区域,根据式(11,14),可得
(13)
由于裂纹i开裂的最终应变能初始表达式为
Uli=U+Eli
(14)
将式(5,11,12)代入式(14)可得
(15)
因此含裂纹梁的刚度为
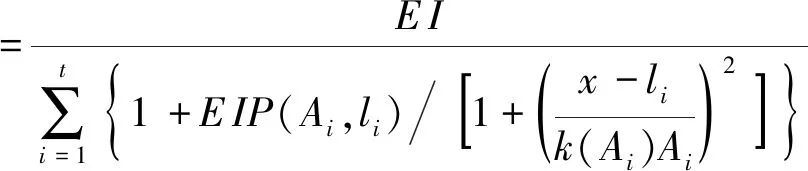
(16)
式中P(Ai,li)与k(Ai)的表达式为
(17)
(18)
4 不同损伤位置、程度和梁截面尺寸对连续梁刚度曲线的影响
可以看出式(16)是关于梁的损伤程度S、损伤位置l及截面尺寸B×h的计算式,因此有必要研究这三个参数对于梁连续刚度曲线的影响。
取长为L=1300 mm的固支钢梁,其参数列入表1,以10 mm为一个单元把梁均匀划分成N=130个单元,损伤为沿梁厚度方向的等高贯通损伤,损伤宽度为单元宽度,S定义为梁刚度的折减,计算如式(19)所示,其中EIn为损伤单元号n的刚度,EI为其损伤前的刚度。
S=1-(EIn)/(EI)
(19)

表1 梁参数Tab.1 Parameters of beam
通过采用控制变量法,分别假定损伤程度、损伤位置和截面尺寸发生变化,通过计算梁连续刚度曲线可以发现,梁连续刚度曲线只受损伤程度的影响,且梁连续刚度曲线是沿损伤位置对称的曲线。根据上述结论可以得知,损伤位置位于小波系数奇异性范围中点,且还可以计算出长为L=1300,均匀划分成130个单元的梁中损伤对周围影响的范围(表2),该范围的对称中心是损伤位置。
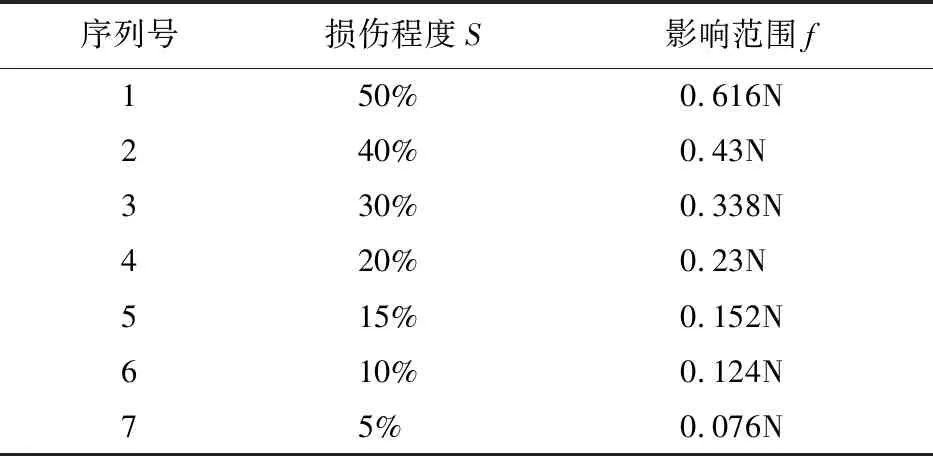
表2 梁单元数N=130个的损伤程度与影响范围Tab.2 Corresponding table of damage severity and influence range of element quantity N=130
5 梁结构损伤位置的精确识别研究
根据第4节损伤位置位于小波系数奇异性范围的中点这一结论,计算损伤结构的小波系数图,通过定位小波系数奇异点范围的中心来确定梁结构的精确损伤位置。
取梁长分别为1274 mm和1300 mm的固支钢梁进行数值模拟与试验,试验中多出的26 mm用于安装传感器,梁的其他参数列入表1。试验采用尺寸为26 mm的圆形振动传感器,因此将梁单元的最小宽度尺寸划分为26 mm,将梁沿长度方向均匀划分为49个单元,设25号单元为损伤单元,损伤程度分别为S=5%和20%。
先利用ANSYS有限元分析软件进行数值模拟分析。通过ANSYS查看梁的第一阶转角模态,利用Matlab进行一阶差分计算出对应的应变模态,再利用Matlab的小波工具箱选用DB3小波对其进行小波变换,可以得到如图2所示25号单元含不同损伤程度的应变模态小波系数图。

图2 含不同损伤程度梁的数值模拟的应变模态小波系数Fig.2 Wavelet coefficients of strain mode in numerical simulation of beams with different damage severities
再将含这两种损伤的梁进行试验,共采用16个传感器用于检测单元节点数据,损伤形状设为沿梁厚度方向的等高贯通均匀损伤,损伤宽度设为26 mm,采用铣床加工而成,加工精度为0.1 mm,试验及损伤设置如图3所示。取第二阶位移模态进行二阶差分得到对应的应变模态,利用Matlab对应变模态进行小波变换,可以得到如图4所示的试验梁应变模态小波系数图。

图3 固支梁试验Fig.3 Experiment of fixed beam
对比图2和图4可以看出,数值模拟与试验得到的小波系数呈现出不同特征的表现形式。数值模拟中应变模态小波系数图显示梁损伤对周围单元的影响只有2~4个;试验中25号单元损伤为5%的应变模态小波系数图奇异性不明显,难以识别出来,而当损伤程度变为20%时,其对应的应变模态小波系数图奇异性非常明显,图中损伤对周围单元的奇异性影响有8个,根据表2反算20%的损伤程度对周围影响为0.23N即11个,虽然存在一定误差,但在可接受范围之内。因此梁的数值模拟分析所得应变模态小波系数图并没有反应梁连续刚度在受损情况下的真实情况,而通过试验可以清楚看到损伤对周围单元的影响范围,且与理论计算出来的结果基本吻合,因此根据损伤位置是小波系数奇异性范围的中心来定位损伤位置。此时试验中梁的损伤位置是小波系数异常范围中点位置,即损伤程度为20%工况的25号单元为受损单元。从而证明了该方法能精确识别试验梁的损伤位置。

图4 试验梁的应变模态小波系数Fig.4 Wavelet coefficient of strain mode for beam experiment with damage severity S =20%
6 结构边界损伤识别研究
取第5节的数值模拟梁进行无损的数值模拟分析。由于试验数据会进行去噪处理,因此数值模拟不考虑加入的噪声影响。如图5(a)所示为该梁的第一阶应变模态小波系数图。从图中可以看到边界位置出现了奇异点,但是边界却没有损伤,这会对损伤识别带来误判。

图5 无损梁的应变模态小波系数Fig.5 Strain mode wavelet coefficient of undamaged beam structural
再对该梁进行试验,取梁长L=1300 mm,试验详情与第5节一致。图5(b)为该无损试验梁的应变模态小波系数图,可以看出,试验梁的应变模态小波系数图与数值模拟梁的图形在边缘都出现了边缘效应,而其他远离边缘位置的小波系数没有出现奇异点。从图5可以看出,边缘位置小波系数奇异点仅限于边缘的第1个点和第2个点,且图2和图4边缘位置的小波系数奇异性也仅限于边缘的第1个点和第2个点。
取第5节的数值模拟梁,分别对梁的第一个单元与第二个单元设置18.7%的损伤程度,可以得到如图6所示的梁第一阶应变模态小波系数图。从图6(a)可以看出,1号单元的小波系数与图2(b)中1号单元的小波系数图形是相似的,只是由于此处出现了损伤,所以图6(a)左端的小波系数大于图2(b)的左端。图6(b)所示为梁的2号单元设置损伤的应变模态小波系数图,可以看到损伤位置出现了奇异性,且其1号单元的小波系数与图2(b)中1号单元的小波系数值基本相等,从而证明了图6(a)中1号单元的损伤确实引起了奇异性。但是直接观察图6(a)无法判断1号单元是否为损伤单元,因此在数值模拟中无法直接利用损伤结构的小波系数图识别边缘损伤。

图6 梁边缘损伤的数值模拟分析小波系数Fig.6 Wavelet coefficient of numerical simulation analysis of damaged beam edge
取第5节的试验梁,在梁的1号单元位置设置18.7%的等高贯通均匀损伤进行试验,如图7所示为该试验梁的第二阶应变模态小波系数图。

图7 梁左边缘含18.7%损伤的试验应变模态小波系数Fig.7 Wavelet coefficients of experimental strain mode with
S=18.7% at damaged beam edge
可以看出,在1~4号点出现了奇异点,因此可疑损伤位置为1~3号单元。假定3号单元为损伤单元,根据表2以及图7的奇异范围反算出3号单元的损伤程度小于5%,而5%以下损伤的小波系数奇异性不明显(即难以识别),因此可以排除3号单元为损伤单元;同理可以排除2号单元为损伤单元。所以损伤位置只能为1号单元,且根据表2反算损伤程度大概为13%,虽然存在误差,但是考虑到试验环境等影响因素,该损伤程度计算结果可以作为初步判断结果。
因此,结合梁连续抗弯刚度以及小波系数的特点,通过排除法可以有效识别结构的边缘损伤。
7 结 论
本文针对结构边缘损伤位置识别问题,以及试验中损伤对周围单元的影响导致小波系数难以精确定位损伤单元问题,提出了基于梁连续刚度与小波变换的结构损伤位置识别方法。该方法不需要结构损伤前的数据,就能准确定位结构的损伤位置,并有效识别结构的边缘损伤。推导了梁连续刚度计算公式,得到了梁中损伤对周边的影响规律,这对梁结构损伤试验中损伤位置的设置具有指导意义,对其他结构的损伤识别具有参考价值。梁的数值模拟与试验分析证明了本文所提方法的有效性,该方法为解决结构边缘损伤位置识别问题提供了一种新方法,为进一步精确定位实际结构的损伤位置提供了理论依据与参考方法。

