高阶思维下高中数学比较大小的方法探究
符晓燕
(江苏省如东高级中学,江苏南通,226400)
2022年高考数学全国Ⅰ卷有许多亮点题型,其中比较大小更值得我们关注.高中数学比较大小除了传统意义的作差、作商、介值、特值、基本不等式、初等函数的单调性等方法外,还可以利用导数的切线、飘带不等式、构造函数、二项式定理、泰勒展开式等比较大小.通过研究近几年的高考试卷,得出如下结论.
1 利用切线不等式比较大小



又y=xex-e(x≥1)单调增,所以xex-e≥0,所以h(x)≥0.



2 利用切线不等式的变形比较大小
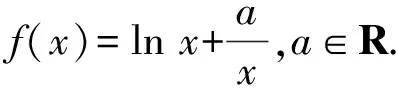
证明:先证,当a>0时,f(x)min=f(a)=lna+1.
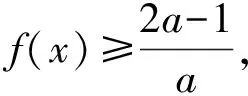
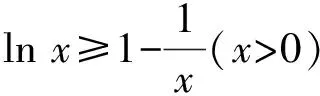
例4已知函数f(x)=aex-1-lnx-1.证明:当a≥1时,f(x)≥0.
证明:∵a≥1,∴aex-1≥ex-1,∴f(x)≥ex-1-lnx-1.
∵x+1≤ex,∴x≤ex-1,∴ex-1-lnx-1≥x-lnx-1≥0,当且仅当x=1时取等号.
对于指数式、对数式、分式这一类问题常利用切线不等式的一些变形、放缩能很快解决一些不等式的比较大小问题,提高效率.
3 利用飘带不等式比较大小
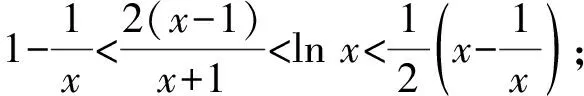
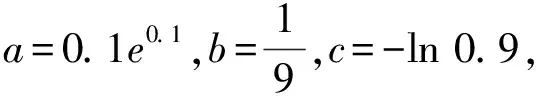
( )
A.a C.c ∴c 证明:可证得当x>-1时,函数f(x)单调增, 由于这些函数在同一直角坐标系中画出来的图象,像飘带,故称为飘带不等式.飘带不等式使用时要注意自变量的取值范围,在不同的范围内,不等式的不等方向可能不同. 例7(八省联考)已知a<5且ae5=5ea,b<4且be4=4eb,c<3且ce3=3ec,则 ( ) A.c C.a 所以f(3) 两种构造方法,异曲同工,效果甚佳. ( ) A.a C.b 当0 ∵h(0)=0,h(0.01)>h(0),∴a>c. ( ) A.e-1B.1 C.eD.e2 解析:由x>0,ax>0⟹a>0, ② 若ax>1,令f(x)=xlnx,f′(x)=1+lnx>0在(1,+∞)恒成立, 对于一些指数式,有时可以用二项式展开式放缩,进而可以比较大小. 再结合飘带不等式比较a与c得正确答案C. 对于指数式中的指数为正整数时,可选取二项式定理放缩.值得注意的是尽量要多写几项,得出的值更逼近原数. 这种方法适用于指数式、对数式、分式的混合式.要对泰勒展开式熟悉的情况下使用,不能对所有的学生适用. 高中阶段对分式、指数式、对数式的混合型比较,在近几年的高考试卷中频繁出现,所以必须要对各种方法熟练掌握,才能自由发挥.


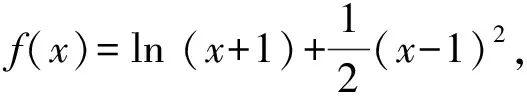
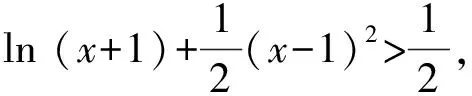

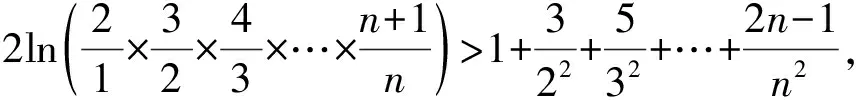
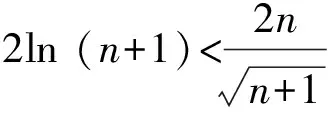

4 通过构造函数比较大小




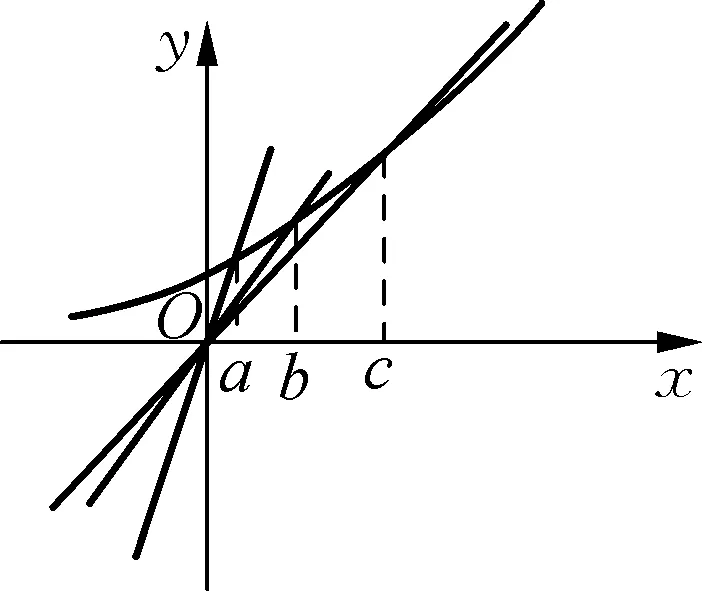
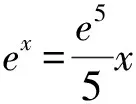

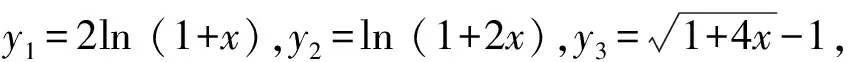
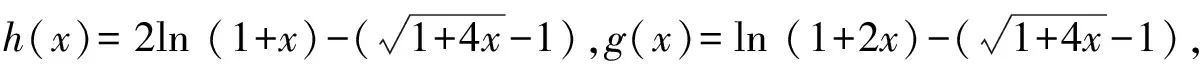




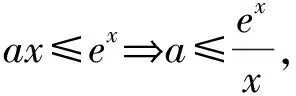

5 通过二项式定理放缩比较大小



6 利用泰勒展开式比较大小




