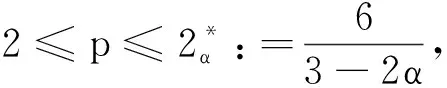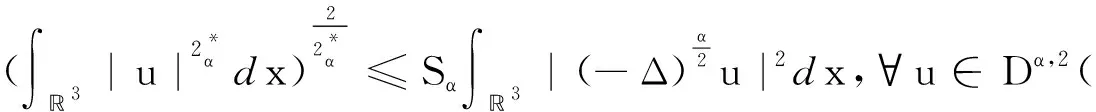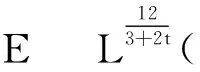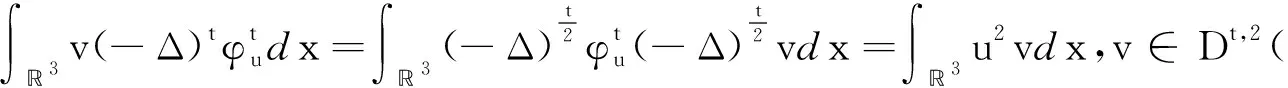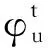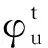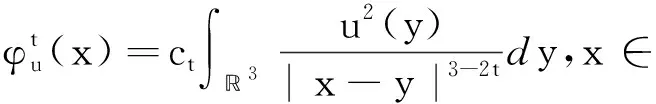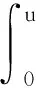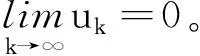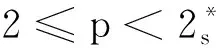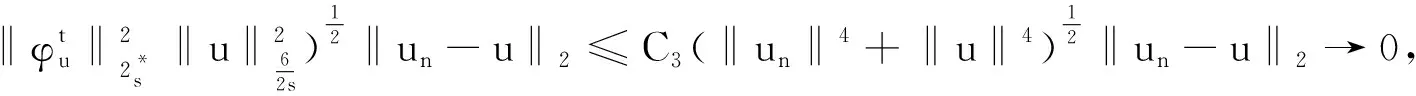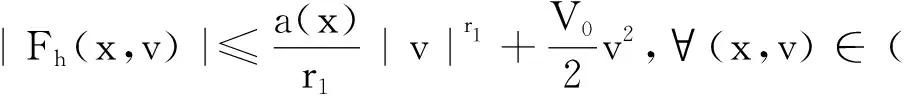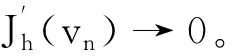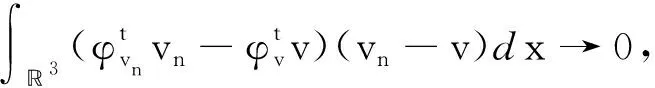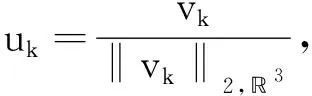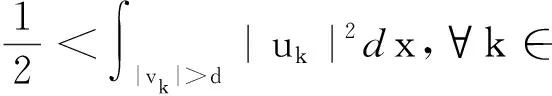分数阶Schrödinger-Poisson系统无穷多解的存在性
胡慧如,黄先玖
(南昌大学数学与计算机学院,江西 南昌 330031)
本文主要讨论以下Schrödinger-Poisson系统
(0.1)
其中(-Δ)α表示分数阶Laplacian算子,其阶数为α∈(0,1),V是可变号的。在(0.1)中,第一个方程是一个非线性分数阶Schrödinger方程,位势函数φ满足一个非线性分数阶Poisson方程。因此,(0.1)被称为Schrödinger-Poisson系统,或又被称为分数阶Schrödinger-Maxwell系统。它不仅是经典非线性薛定谔方程(NLS方程)在物理上的相关推广,也是分数阶量子力学中的一个重要模型。关于更多的物理背景可参阅文献[1-3]及其参考文献。
众所周知,分数阶Schrödinger-Poisson系统是由Giammetta[4]首次提出的,扩散项仅在Poisson方程中是分数阶的。之后,文献[5]在V(x)≡0且非线性项f(x,u)呈次临界或临界增长时证明了方程(0.1)径向基态解的存在性。另外,文献[6]在V(x)为正的情况下,利用喷泉定理证明了方程(0.1)无穷多个解的存在性。
近年来,下面的变号位势函数开始被研究:
(V1)V∈C(3,)且
许多学者研究了带有上述变号位势及具有不同增长条件的Schrödinger方程无穷多解的存在性,例如文献[7-8]。在前人工作的基础上,又有许多学者在同样的情况下,研究了不同方程的无穷多解。例如,文献[7-18]及其参考文献。特别地,Zhou[8]和Bao[9]讨论了带有变号位势的Schrödinger-Poisson方程无穷多个小能量解的存在性。然而,很少有文献通过对偶方法处理分数阶Schrödinger-Poisson系统。
借鉴文献[8-9]中的方法,我们将对V和f做以下假设,讨论方程(0.1)在局部非线性条件下无穷多个小能量解的存在性:
(V2) 对∀M>0,有
meas{x∈3:V(x)≤M}<+∞,
(f1) 存在常数δ1>0和1 |f(x,t)|≤a(x)|t|r1-1,|t|≤δ1,∀x∈3, (f3) 存在常数δ2>0,使得对任意的|t|≤δ2和x∈3有f(x,-t)=-f(x,t)。 下面,我们给出本文的主要结论。 且当k→∞时uk→0。 在本文中,C>0表示不同的正常数。 在陈述这一节内容之前,需要注意以下事实:通过(V1)可得,存在一个常数V0>0使得对任意的x∈3有令并考虑下面的方程 (1.1) 为了证明结论,首先定义Gagliardo半范数为 其中u:3→是一个可测函数。 接下来,定义分数阶Sobolev空间 Wα,p(3)={u∈Lp(3):u可测且[u]α,p<∞} 赋予范数 (1.2) 当p=2时,空间Wα,2(3)与Fourier分析意义下的分数阶Sobolev空间是等价的,即, Hα(3):=Wα,2(3)= 赋予范数 ‖u‖Hα= 等价。 假设Lp(Ω)是一个Lebesgue空间,将Lp(Ω)中的范数记为|·|p,Ω,其中Ω⊆3,1≤p≤+∞。令3和Hα(3)表示通常的分数阶Sobolev空间(见文献[19])。在假设下,定义工作空间为 (1.3) 和 因此,E是一个内积为 (u,v)EV= (u,v)E,Ω= 范数为 的Hilbert空间。此外,‖·‖EV和‖u‖E,Ω分别与范数 ‖u‖:=‖u‖E= 和 ‖u‖E,Ω= 等价,且相应的内积为 (u,v)E= 和 (u,v)E,Ω= 齐次Sobolev空间的定义为 Dα,2(3)= 和内积 (1.4) 受文献[20]中引理3.4的启发,我们可以用同样的方法证明下面的引理2.1。 引理2.2[19]对任意的α∈(0,1),Dα,2(3)连续嵌入3)。即,存在Sα>0使得 (2.1) (2.2) 其中 则对任意的x∈3有由(2.1)和(2.2)可得,当2t+4s≥3时,有 (2.3) 接下来,定义截断函数h∈C1(,)满足以下条件:0≤h(t)≤1;当t∈时h(-t)=h(t);当|t|≤d时h(t)≡1;当|t|≥2d时h(t)≡0;当t∈[d,2d]时h(t)单调递减。其中,令 fh(x,u)=f(x,u)h(u),∀(x,u)∈3× (2.4) 且 (2.5) 考虑下面修正的分数阶Schrödinger-Poisson系统 (2.6) 其能量泛函为 Jh(u)= Jh的Gateaux导数为 (2.7) 令Γk表示E的闭的对称子集A的族,其中A满足0∉A且γ(A)≥k。下面的临界点定理来自于文献[21]。 引理2.3[21]设E是一个无限维Banach空间,Jh∈C1(E,)是一个满足Jh(0)=0的偶函数。假设Jh满足 (J1)Jh下方有界且满足(PS)条件; (J2) 对任意的k∈,存在Ak∈Γk使得 引理2.4假设序列{un}⊂E满足:当n→∞时un⇀u在E中成立,{‖un‖}是一个有界序列。则当n→∞时,有 (2.8) 证毕。 引理2.5假设(V1)-(V2)和(f1)-(f2)成立,则Jh下方有界且在E上满足(PS)条件。 证明根据(V1)-(V2),(f1)-(f2)和h的定义,可以得到 对任意给定的v∈E,令Ω={x∈3:|v|≤1},由r1∈(1,2),Hölder不等式和Jh的定义可得 (2.9) 这说明‖vn‖E,Ωn≤C且C与n无关。因此, (2.10) 其中,C与n无关。类似地, 因此, (2.11) 其中,C与n无关。结合(2.10)和(2.11),有 有界,且与n无关。则根据引理3.1[22]的证明可得 利用(f2)和Hölder不等式可得, (2.12) 利用引理2.4,又得到 (2.13) 结合(2.12)和(2.13)可得 因此vn→v在E中成立。 证毕。 类似引理3.2[9]和引理3.2[23]的证明,可以得到下面的引理。 引理2.6对任意的k∈存在一个闭的对称子集Ak⊂E,使得γ(Ak)≥k且 证明令En表示E的一个n-维子空间。由于有限维空间中的所有范数都是等价的,故存在常数β=β(En),使得对任意的v∈En有 ‖v‖≤β‖v‖2 其中‖·‖2是L2(3)中的常用范数。 接下来断言,存在一个常数M>0,使得对任意的v∈En和‖v‖≤M有 (2.14) 事实上,若(2.14)不成立,则存在一个序列{vk}⊂En{0}使得vk→0在E中成立,并且对任意的k∈有 (2.15) 另一方面,由于En是有限维的,则可假设uk→u在E中成立。因此uk→u在L2(3)中成立。又由vk→0在E中成立可得 meas{x∈3:|vk|>d}→0,k→∞。 因此, 这与(2.15)矛盾,故(2.14)成立。由(f1),可取d充分小,使得对任意的x∈3和0≤v≤2d有 从而有 Fh(x,v)=F(x,v)≤ (2.16) 又因为假设(f3)表明Fh(x,v)关于v是偶的,所以由(2.16)可得,对任意的v∈En, 其中‖v‖≤min{M,1}。令0<ρ≤min{M,1},An={v∈En:‖v‖=ρ},可以推出γ(An)≥n且 证毕。 定理1的证明由(f1)-(f3)可知Jh是偶的且Jh(0)=0。则由引理2.5和2.6可得Jh有一个临界点序列{uk},使得Jh(uk)≤0,以及当k→∞时uk→0。另外,类似引理5.1[24]的证明可得,存在k1使得当k≥k1时有|uk|∞,3≤d。因此,我们得到(0.1)的无穷多个小能量解。 证毕。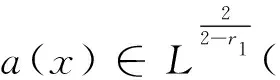
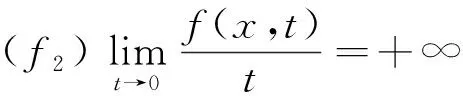

1 变分框架

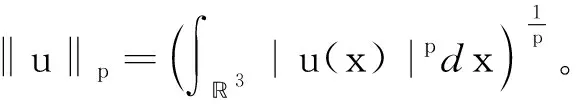

2 引理和结论