基于拉普拉斯算子和颜色保留的神经风格迁移算法
谭永前,曾凡菊
(凯里学院 大数据工程学院,贵州 凯里 556011)
0 引言
图像的风格化绘制是指把一幅图像的风格(画风),通过相应的算法迁移到另一幅内容图像上,使得内容图像不仅保留了原图像的内容,还具有了风格图像艺术风格的过程。对图像进行风格化绘制,源自于人们对某些绘画大师艺术作品风格的热爱和吸引,人们渴望像这些绘画大师一样绘制出某种艺术风格的绘画作品,于是便开始利用计算机算法去模拟实现某种图像风格并进行风格迁移。近年来,随着研究者们在深度学习方面的不断探索和研究,Gatys等[1]在2015 年开创性地提出把卷积神经网络(Convolutional Neural Network,CNN)用于图像的风格迁移,提出了一种基于CNN 的图形图像风格化转换算法。基于CNN 的图像风格迁移通过在深层CNN 中提取图像高级抽象特征来实现特征空间的分布匹配,图像风格化取得了很好的效果。2016年,Gatys等[2-3]又提出了基于CNN 的图像风格迁移(Image Style Transfer using Convolutional Neural Networks,IST-CNN)算法,在图像处理领域引起了广泛的关注。谢斌等[4]针对图像的特征执行相关对齐,提出基于相关对齐的风格迁移模型。Kotovenko等[5]在对抗网络中设计了一个内容转换模块,用于在具有相似语义内容信息的内容图像和风格图像之间的风格迁移过程中学习如何改变内容图像的细节,该算法更关注于图像的内容和风格感知风格化。Cheng等[6]加入了边缘检测网络来保护图像的局部细节结构,权衡地保留生成图像的全局和局部结构。Wang等[7]提出了基于深度特 征扰动(Deep Feature Perturbation,DFP)算法,在深度特征变换中加入正交噪声矩阵来扰动风格迁移过程,这种方式能在不影响原有风格迁移质量的条件下,显著地提升生成图像纹理的多样性。
基于CNN 实现图像风格化算法存在如下不足:1)Gatys等[1-3]在进行风格转换时仅仅把颜色作为特征感知方面的重要特征,导致图像风格化的结果不够稳定;2)谢斌等[4]和Li等[8]在进行风格迁移时把风格图像作为一个整体进行了迁移,导致风格化后的结果图像中部分颜色匹配杂乱,产生了混色问题;3)Cheng等[6]和Wang等[7]在使用CNN 提取图像的高层次特征时,丢失了一些低层次的细节信息,导致结果图中部分有扭曲变形、模糊不清的情况;4)很多基于CNN 的神经风格算法[5-8]使用格拉姆(Gram)矩阵对图像特征进行表示时,图像中会出现伪影(包含原图没有的细节及影响视觉效果的规则纹理)现象。
基于CNN 的图像风格迁移算法在提取图像特征时都是在高层次的CNN 特征空间中完成的,虽然这样做的结果在感知效果上优于在传统像素空间计算的特征,但由于特征空间是对图像的一种抽象表达,会不可避免丢失一些低层次图像特征信息,比如图像的边缘特征信息等,这会直接导致风格化结果图中局部内容的细节丢失。
本文提出了基于拉普拉斯算子和颜色保留(Laplacian operator and Color Retention,LCR)的神经风格迁移算法。本文的主要工作如下:1)把直方图也作为图像细节特征控制的一个维度,通过计算内容图像与风格化结果图像之间的直方图损失,把直方图损失作为总损失函数的一部分,以提高图像风格化的稳定程度;2)通过颜色空间转换,将内容图像的颜色迁移至风格图像,避免了文献[2,6-7]等风格化算法在风格化过程中丢失内容图像颜色信息,产生颜色杂乱、混色等情况;3)计算内容图像与风格化图像之间的拉普拉斯损失项,并把两者的拉普拉斯损失项也作为总损失函数的一部分,以此来改善风格化结果中扭曲变形、模糊不清以及伪影等问题。以上工作很好地提高了风格化图像的稳定性,保留了内容图像的颜色信息,有效地抑制了伪影,减少了扭曲、变形,也保证了风格迁移的视觉效果,使得整体艺术风格和颜色亮度信息细节处理上得到有效改善。
1 基于深度学习的图像风格化
自从Gatys等[1]提出将CNN 应用于图像风格化处理以来,神经网络以其能快速提取图像高级抽象特征的优势、强大的多层次图像特征和语义表征能力,被广泛应用于图像特征提取,近年来逐渐成为图像风格迁移领域的基本技术。Gatys等[1]使用基于CNN 的VGG19 模型[9]进行特征提取并实现风格迁移,VGG19 模型由16 个隐藏层加3 个全连接层组成,VGG16 模型由13 个隐藏层加3 个全连接层组成,两者在结构上没有本质的区别。VGG16 模型如图1 所示,风格迁移算法实现的流程[2]如图2 所示。
本文仍然采用VGG19 模型进行训练,为了提升图像的生成质量,在全连接层采用效果更好的Mish[10]激活函数替代线性整流函数(Rectified Linear Unit,ReLU)。图2 中左边输入图像为风格图像,右边输入图像为内容图像,中间为生成的风格化结果图像。图2 中各符号意义见文中各定义描述。
定义1总损失函数Ltotal。Ltotal的定义如下:
其中:LC表示目标内容图像的损失函数;LS为风格图像的损失函数;α、β分别表示在生成风格化图像的过程中目标内容图像和风格图像的权重调节因子。改变α和β的比重,会影响风格化结果图的效果:如果α较大且β较小,生成的风格化结果图就比较偏向于内容图;如果β较大且α较小,生成的风格化结果图就比较偏向于风格图。实验中可根据需要选择α/β的值达到控制风格迁移程度的目的。
定义2目标内容图像的损失函数LC。LC的定义如下:
其中:Fl与Pl分别表示随机噪声图像与目标内容图像在l层的特征表示。
定义3风格矩阵使用格拉姆矩阵定义如下:
其中:等于随机噪声图像在CNN 中第l层第i个卷积核与第j个卷积核输出激活项的积。
定义4风格图像第l层的风格损失函数El定义如下:
其中:Nl表示在第l层中卷积核的个数;Ml表示在第l层的特征图的大小即高乘以宽;与分别表示随机噪声图像和风格图像在CNN 中第l层第i个卷积核与第j个卷积核的输出激活项。则在CNN中,风格图像所有层的风格损失累计为:
其中:表示输入的原始风格图像;表示初始化的噪声图像;wl表示风格图像每个卷积层对风格图像总损失函数的贡献权重因子;L表示CNN 的总卷积层数。
定义5风格图像第l层的风格损失函数El对求导可得到:
其中:Fl表示目标内容图像特征表示过程中初始化的噪声图像在第l层的响应值;Gl、Al分别表示在风格图像特征表示过程中初始化的噪声图像和输入的风格图像在第l层的响应值。
2 本文算法
在实际中,图像的颜色和亮度信息特征不同于图像的其他风格特征,图像的颜色和亮度信息是其在特征感知方面的重要特征;同时,人类的视觉感知系统对图像亮度变化的敏感程度要远高于对颜色变化的敏感程度[11-12],因此在分析和处理图像时,其亮度信息应该作为图像风格的细节变化和细节纹理特征的重要表述。基于上述原因,图像的颜色信息特征和亮度信息特征都可以作为风格迁移网络的重要感知特征,成为图像风格化过程中不可或缺的控制纬度。本文在风格化迁移过程中融入图像的直方图损失和颜色亮度信息,可以使风格化结果在整体艺术风格以及颜色亮度信息细节处理方面得到有效改善,下面将分别进行详细阐述。
2.1 直方图损失
在Gatys等[1-3]提出的基于CNN 实现图像风格化的相关算法中,求解风格损失时都采用了格拉姆矩阵作为风格矩阵,格拉姆矩阵可以看作特征向量之间的偏心协方差矩阵。格拉姆矩阵计算两两特征的相关性,这种相关性是通过矩阵的内积来展示的,但可能存在两幅完全不同的图像却存在相同的格拉姆矩阵的情况,如图3 所示。图3(a)是一个分布均匀的灰度图形,均值μ=0.7,方差σ=0;图3(b)是一个分布不均匀的灰度图,均值μ=0.5,方差σ=0.5。这两个灰度图形均值和方差都不一样,但如果把它们看作是特征映射的激活,那么这两个图形的格拉姆矩阵却是一样的。所以把格拉姆矩阵作为风格损失函数唯一的控制维度,无法准确地反映对图像细节特征的描述。
图像的直方图是计算统计图像信息的一种重要手段,由于其计算代价较小,具有图像平移、旋转、缩放后仍然保持不变性等众多优点,被广泛应用于图像处理领域。本文把直方图也作为图像细节特征控制的一个维度,把内容图像与风格化图像之间的直方图损失作为总损失函数的一个部分。加入直方图损失项的主要作用是提高图像风格化的稳定性。
定义6定义Oi表示第i个特征映射,R(Oi)表示与原风格图像匹配后得到的特征映射,直方图损失Lhis可表示为:
其中:L表示CNN 的总卷积层数;γl表示各个网络层在直方图损失中所占的比例;‖ · ‖表示范德蒙距离。
2.2 颜色保留
传统基于神经网络的风格化绘制算法在风格化结果图中,部分生成的结果中出现了颜色混乱不搭的情况,视觉效果上影响了风格化的整体艺术效果。本文受到颜色迁移相关算法[13-14]的启发,在图像风格化过程中利用对颜色和亮度的迁移来保留内容图像的颜色细节信息和亮度细节信息。
定义7定义XC表示输入的内容图像,XS表示输入的风格图像,XJ表示颜色匹配迁移后的图像,xi=(R,G,B)T表示输入内容图像和输入风格图像的像素颜色。把内容图像XC的颜色匹配迁移到风格图像XS上,得到新的图像XJ,则迁移前后像素值有如下的数学映射关系:
其中:A表示一个3×3 的矩阵;b表示一个3×1 的向量;xS表示输入风格图像的像素值;xCJ表示颜色迁移后的像素值。
要得到颜色匹配迁移后的像素值xCJ,必须先确定矩阵A和向量b,下面将详细阐述。
定义8定义μC、μS分别表示在RGB 颜色空间中,输入内容图像和输入风格图像每个像素的均值;σC、σS分别表示输入内容图像和输入风格图像的协方差。根据均值与协方差的定义可得到:
把内容图像XC的颜色匹配迁移到风格图像XS上后,得到新的图像XJ时,必需满足XJ的像素颜色均值以及像素协方差与XC的像素颜色均值和像素协方差保持一致,即
其中:μCJ表示颜色迁移后图像XJ的均值;σCJ表示颜色迁移后图像XJ的协方差。
根据式(10)~(12)可以得出矩阵A和向量b的数学关系式如下:
由式(13)以及数学方面的知识可以看出,向量b的值由矩阵A确定,只要确定了矩阵A,就能确定向量b。由矩阵方面的知识可知,满足式(13)的矩阵A有很多个,本文在求解矩阵A时,参考文献[15]中的图像类比的方法求解。首先,协方差矩阵的特征值可以分解为:σ=UAUT;然后,通过计算可得到矩阵的平方根为;最后,通过公式变换可以得出矩阵A的值。通过以上数学思路,本文将内容图像的颜色成功匹配迁移至风格图像,避免了传统风格化算法在风格化过程中丢失内容图像颜色信息的情况。
在Lab 颜色空间中,每个像素的颜色值都被分离为一个亮度通道L 和两个颜色通道a、b,这为进行颜色亮度的分离提供了条件。本文在Lab 颜色空间把内容图像的亮度和风格图像的亮度单独提取出来,并将内容图像的亮度信息迁移至风格图像,以实现内容图像亮度信息与风格图像亮度信息匹配,达到保留内容图像颜色的目的,以此来改善传统神经网络风格化算法结果图中出现颜色混搭的问题。
定义9定义HC和HS分别表示内容图像和风格图像的亮度通道;HJ表示进行亮度迁移后风格图像的亮度像素;BC和BS分别表示内容图像和风格图像的亮度均值;dC和dS分别表示内容图像和风格图像的标准差,则内容图像到风格图像的亮度迁移可用式(13)表示:
2.3 拉普拉斯算子和损失
传统神经风格迁移算法在计算内容损失时,使用CNN提取特征,然而这些特征属于高层次的代表,主要是捕捉的内容图像的语义信息;然而这样便不可避免地损失了一些低层次的细节信息,比如细节纹理、边缘基本结构信息等,因此,得到的结果图像会出现一些不规则的扭曲和形变以及伪影。为了在风格化结果中减少扭曲、变形以及伪影,并更好地保留内容图像的细节信息,本文引入拉普拉斯损失项来解决这个问题。
拉普拉斯算子是二阶微分线性算子,在图像边缘处理中,二阶微分的边缘定位能力更强,锐化效果更好,能够找到图像像素的过渡程度。因此,在进行图像边缘处理时,对图像进行拉普拉斯变换可以增强图像边缘,有利于提取目标的边缘,对图像进行分割、目标区域识别、区域形状提取等[16-17]。本文把在像素空间中内容图的拉普拉斯算子的滤波结果和风格化重建结果图的滤波结果之间的差异作为一个新的损失项,弥补了抽象特征空间丢失低层次图像信息的缺点。
在二维情况下,拉普拉斯算子的定义为:
其中:f(x,y)表示一个二维函数,x与y代表x-y平面上的笛卡儿坐标。在一个二维函数f(x,y)中,x、y两个方向的二阶差分分别为:
根据式(14)得到拉普拉斯在二维情况下算子的离散形式为:
写成模板的形式如下:
本文计算拉普拉斯损失项的方法如下:对于输入的内容图像xC和风格化结果图像x→对应的拉普拉斯变换分别为D(xC)和D(),则拉普拉斯损失项为:
则本文采用新的风格迁移总损失函数为:
其中:α、β和γ为后三个损失函数项的权值。
2.4 本文算法实现步骤
本文把内容图像与风格化图像之间的直方图损失项以及拉普拉斯损失项作为图像风格化细节特征的控制维度加入到总损失函数中,同时还综合考虑了内容图像和风格图像的颜色亮度信息对风格化视觉效果的影响,在Gatys等[2]算法基础上提出了基于拉普拉斯算子和颜色保留的神经风格迁移算法,所提风格化迁移算法的示意图如图4 所示。
具体实现步骤如下:
1)输入内容图像和风格图像并对其进行去噪处理,减小噪声对后续各个损失项计算的影响。
2)对内容图像和风格图像进行RGB 空间到Lab 空间的转换,实现图像亮度通道L 和颜色通道a、b 的分离,把内容图像的亮度信息迁移到风格图像上,保留了内容图像的颜色信息。
3)把进行亮度迁移后的内容图像和初始化的风格化结果图输入到CNN,并进行内容损失项的统计,获得内容图像的损失函数,如式(2)。
4)统计拉普拉斯损失项,如式(19);统计直方图损失项,如式(9)。
5)计算去噪后风格图像的风格损失函数,如式(6)。
6)构造新的总损失函数,如式(20),并在CNN 中不断迭代优化,利用梯度下降法进行不断迭代,输出风格化结果图。
在进行风格迁移过程中,各个损失项的计算是同时进行的,即第3)~5)步是同时进行各损失项计算的。
3 实验与结果分析
3.1 实验环境平台
本文所有实验均使用VGG19 模型进行网络训练,选取的目标内容图像来自MS-COCO 数据集,风格图像来自WikiArt 数据集。实验训练过程中设定参数batch_size 为4,epoch 为2,优化器采用Adam 进行迭代优化,其他相关参数设置如表1。利用CNN 的conv4_2 的输出作为内容损失函数的定义,利用“conv1_2”“conv2_1”“conv3_1”“conv4_1”“conv5_1”的输出作为风格损失函数的定义。实验在Ubuntu16.04,64 位操作系统中进行,显卡为英伟达GTX960,采用版本1.4.0 的Tensor flow 深度学习平台,使用Python 3.6.2 语言实现编程及CUDA9.2 等相关软件工具包。实验中使用的图像大小均以像素为单位。
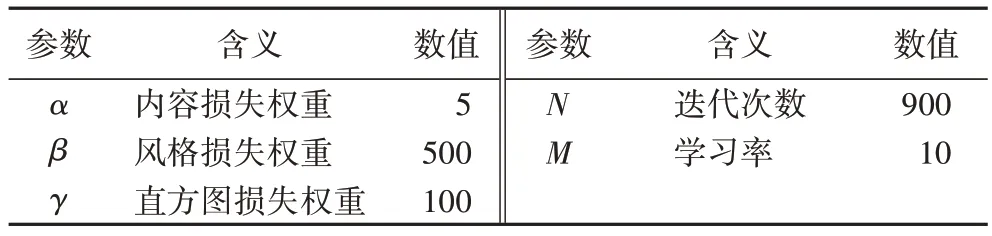
表1 主要参数Tab.1 Main parameters
3.2 实验结果分析
为了验证本文算法增加直方图损失项、拉普拉斯损失项以及采用颜色保留方法的效果,设置了4 组实验进行验证:1)采用总损失函数式(1)进行迭代,并使用本文算法的颜色保留方法,实验效果对比如图5 所示。2)在总损失函数式(1)中加入直方图损失项,实验效果对比如图6 所示。3)在总损失函数式(1)中加入拉普拉斯损失项,实验效果对比如图7 所示。4)采用本文算法的总损失函数式(20)进行迭代,并采取颜色保留方法,实验结果对比如图8 所示,图8所用相关图像的参数见表2。
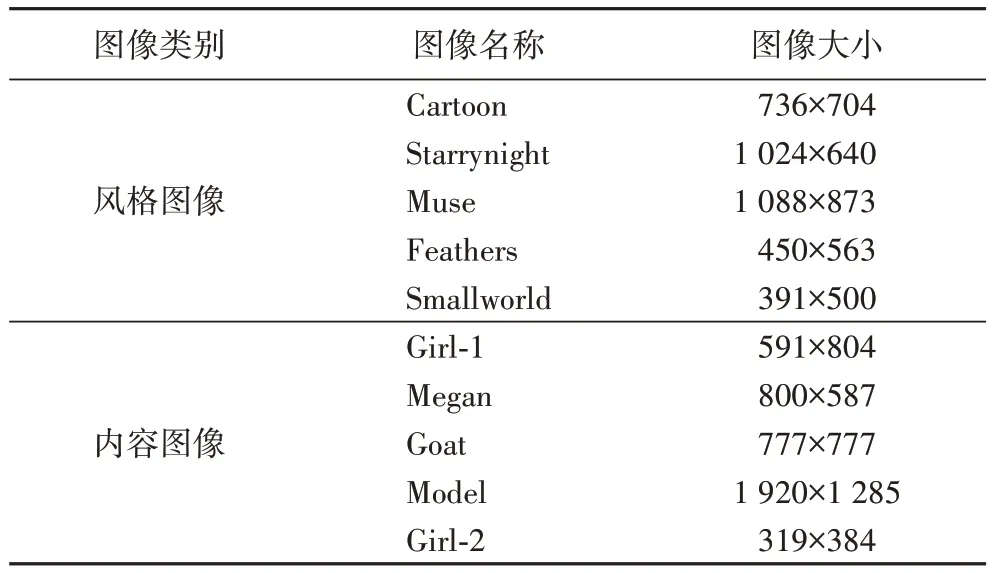
表2 实验图像参数Tab.2 Experimental image parameters
图5 是风格迁移过程中进行颜色保留和没有进行颜色保留的实验结果对比。从图5 的Afghan girl 实验中可看出IST-CNN[2]、文献[5]算法、DFP[7]得到的风格迁移实验结果在背景、头巾以及脸等地方的颜色完全被风格图像的颜色所代替,并且出现了很大的扭曲变形,只有本文算法在上述地方都很好地保留了原内容图像的颜色信息,并且很好地继承了风格图像的“画风”,图像的清晰度也比对比算法要好。在Bedroom 实验结果中,IST-CNN、文献[5]算法、DFP 在地板、沙发、被子以及墙壁等地方的颜色信息被风格图像的颜色所代替,本文算法在以上地方都很好地保留了内容图像的颜色,并且没有产生马赛克伪影。实验结果表明,本文算法生成的风格图像质量最好,很好地保留了内容图像的颜色信息。
图6 是采用本文在损失函数中加入直方图损失项与没有加入直方图损失项的实验结果对比。从图6 的Ship 实验和Model 1 的实验结果中可以看出,IST-CNN、文献[6]算法在Ship 实验的虚线框区域内出现了马赛克伪影,在黑色框区域内效果表现也较差;IST-CNN、文献[6]算法在Model 实验的虚线框区域嘴唇部分,产生了伪影、混色、牙齿和嘴唇不清晰等问题,本文算法在上述区域表现更好。文献[6]算法在风格迁移网络中加入了边缘检测网络来保护图像局部细节结构,保护了生成图像的全局和局部结构信息,整体生成效果要好于IST-CNN。本文算法在总损失函数中增加直方图损失项作为图像细节特征控制的一个维度,提高了图像风格化的稳定性。
图7 是本文加入拉普拉斯损失项与传统算法代表(文献[6]算法、DFP)实验结果对比,其中,3 幅内容图像的背景复杂度各有不同。在图7 虚线框区域内,文献[6]算法、DFP都产生了马赛克伪影,在白色框区域内有变形、扭曲的问题存在,在黑色框区域内存在混色、模糊不清等问题。文献[6]算法得益于加入了边缘检测网络,所以在图像的细节保留方面要好于DFP;而DFP 在深度特征变换中加入正交噪声矩阵来扰动风格迁移过程,相较于文献[6]算法,显著地提升了生成图像纹理的多样性,所以DFP 生成的图像在纹理变化多样性方面要好于文献[6]算法。本文算法加入了拉普拉斯损失项,有效抑制了马赛克伪影的产生,以及扭曲变形,在图7 的实验结果中本文算法结果的质量最高。
为了从整体视觉效果上进行比较,设置了Girl-1_Cartoon、Megan_Starrynight、Goat_Muse、Model_Feathers、Girl-2_Smallworld 几组实验进行对比。图8 实验结果对比中,IST-CNN 的实验结果把风格图像的整体风格和颜色信息都迁移到内容图像上,风格图像的颜色完全覆盖了内容图像的颜色,使得风格化后的图像丢失了部分原内容图像的相关颜色信息,导致风格化绘制后的图像模糊不清,无论是对内容图像的颜色保持,还是整体的艺术效果都比较糟糕,这也是早期基于CNN 图像风格迁移算法普遍存在的不足。基于IST-CNN 的不足,DFP 在IST-CNN 的基础上进行了相关的改进,DFP 在深度特征变换中加入正交噪声矩阵来扰动风格迁移过程,这种方式能在不影响原有风格迁移质量的条件下,显著地提升生成图像纹理的多样性和质量,使得实验结果在获得风格图像一些风格特征的同时,也保留了内容图像的部分颜色,图像也更加清晰,视觉上的整体艺术效果得到了一定的改善。本文利用在像素空间中计算内容图与风格图的拉普拉斯损失和直方图损失,把两者作为总损失函数控制的一部分来消除伪影、扭曲变形和提高风格化稳定度;同时,利用颜色亮度迁移的方法实现内容图像的颜色保留。本文算法有效抑制了伪影,避免了扭曲变形,图像的细节信息也保存较好,清晰度也更高。
为了进一步验证本文算法在处理风格化图像细节方面的有效性,对图8 中风格化绘制结果局部进行了放大对比,对比结果如图9 所示。
从图9 的局部放大对比可以看出:IST-CNN 得到的风格化绘制通过局部放大后,头发、嘴唇和鼻子的轮廓都非常地模糊,出现了伪影,扭曲,影响了风格化的最终视觉效果,如图9(b)所示;DFP 得到的风格化图像较IST-CNN 的图像要清晰很多,但仍然存在一些模糊和线条扭曲的情况,如图9(c)所示;本文算法得到的风格化绘制图像经过局部放大后轮廓比较清晰,没有出现伪影和扭曲的问题,比IST-CNN 和DFP有更好的细节处理效果。
3.3 实验结果评价
从图8 可看出:从主观视觉效果上来比较,本文算法得到的风格化绘制结果在整体艺术视觉效果上要好于ISTCNN 和DFP。从图9 局部放大对比结果中同样可看出,本文算法得到的风格化绘制图像,从主观视觉效果上风格化绘制的细节处理效果也要好于IST-CNN 和DFP。客观评价方面目前还没有形成一个统一的客观度量标准去衡量风格化绘制图像质量的好坏,很多学者都采用风格化绘制图像的峰值信噪比(Peak Signal-to-Noise Ratio,PSNR)、结构相似性(Structure SIMilarity,SSIM)以及均方差(Mean Square Error,MSE)等指标来衡量风格化图像质量的好坏[15]。本文将从PSNR、SSIM 和MSE 三个指标上对风格化绘制结果的质量进行客观评价,用算法运行时间来评价风格化绘制的效率。PSNR 用来衡量图像的生成质量,SSIM 用来衡量图像的结构相似性,PSNR 和SSIM 的值越大,说明风格化图像的质量越高。MSE 用来衡量图像各数据偏离真实值的距离,MSE 值越小表示图像各数据越接近真实值。表3 对图8 中各组实验的评价指标进行了统计。
表3 统计了图8 中IST-CNN 和DFP 以及本文算法生成风格化绘制图像的PSNR、SSIM、MSE 以及算法运行时间。表3中本文算法得到的风格化绘制图像与原内容图像的均方差最小,与IST-CNN 和DFP 相比,本文算法均方差平均降低了0.653 76 和0.296 00,说明风格化绘制图像的数据与真实值越接近,这与图8 中的整体主观视觉效果反映一致。表3 中本文算法峰值信噪比与IST-CNN 和DFP 相比,平均提高了约12.418 dB 和8.038 dB。表3 中本文算法结构相似性与ISTCNN 和DFP 相比,平均提高了约0.348 06 和0.258 54。本文算法得到的风格化绘制图像的PSNR、SSIM 在每一组实验中都最高,说明本文算法得到的图像质量要好于IST-CNN 和DFP,这与图8 中的整体主观视觉效果评价保持一致。表3是每组实验算法运行时间的统计比较,本文算法运行时间与IST-CNN 和DFP 相比,平均高出7.4 s 和16 s。这是因为本文算法增加了去噪处理、直方图损失项和拉普拉斯损失项的计算,消耗了一定的时间代价,在总的运行时间效率上比IST-CNN 和DFP 要低,但本文算法以较小的时间代价获得了更好的整体视觉效果。
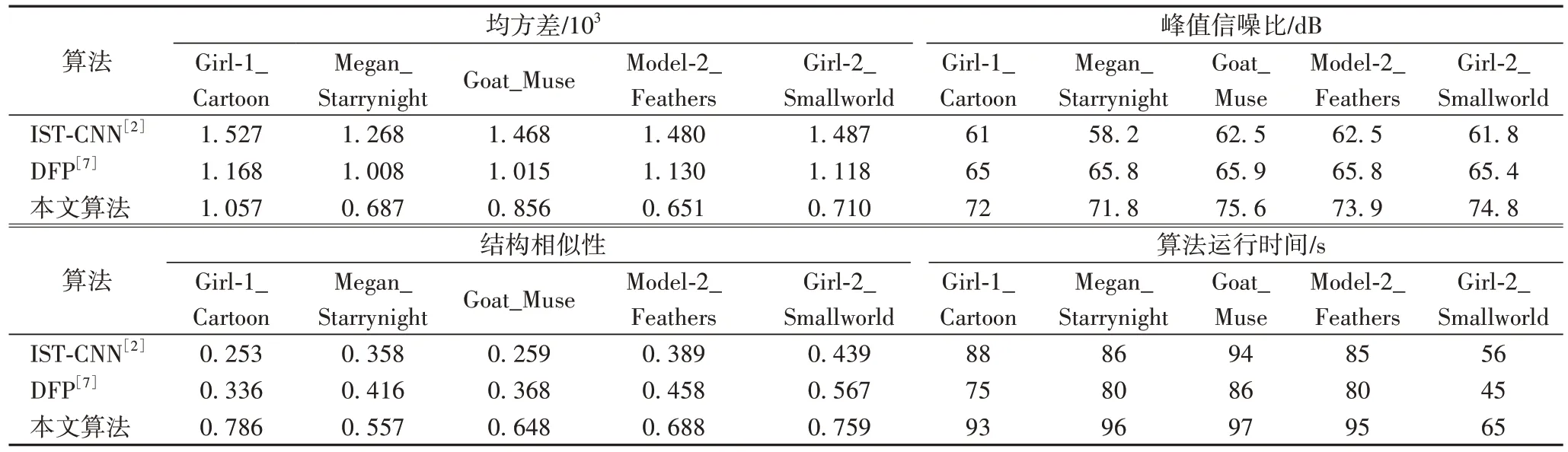
表3 评价指标统计Tab.3 Evaluation index statistics
4 结语
本文在总结分析了传统基于CNN 风格化图像绘制相关算法后,在基于CNN 风格化处理算法基础上进行了改进,通过综合考虑图像的直方图在图像统计信息中的重要性以及人类对颜色亮度的敏感性,提出了加入直方图损失和颜色保留亮度的图像风格化绘制算法;同时为了弥补IST-CNN、文献[6]、DFP 等算法在抽象特征空间丢失低层次图像信息的问题,本文提出在像素空间中将内容图的拉普拉斯算子滤波结果和风格化重建结果图滤波结果之间的差异作为总损失函数的一部分,加入拉普拉斯算子可以在一定程度上消除伪影、防止局部信息丢失,减少扭曲、变形。本文算法更好地保留了内容图像的颜色信息,使风格化整体艺术效果和颜色亮度信息细节处理得到有效改善。
通过与传统相关算法的实验结果进行比较,本文算法在图像风格化过程中,在能较好地保留内容图像颜色的同时也能在细节纹理的处理方面取得比传统相关算法更好的效果。在利用PSNR、SSIM,以及MSE 指标对风格化绘制图像进行客观评价时,本文算法在指标上表现更好。本文算法在算法时间运行效率上还存在一定的不足,算法还有优化提升的空间。不断优化算法,更进一步提高算法的运行效率,将是今后努力的一个重要方向;同时,构建和完善风格图像客观评价的统一标准,也将是今后研究的一个重要方向。

