基于差分隐私的高精度直方图发布方法
李昆明,王超迁,倪巍伟*,鲍晓涵
(1.江苏方天电力技术有限公司智能电网服务中心,南京 210000;2.东南大学计算机科学与工程学院,南京 211189)
(∗通信作者电子邮箱wni@seu.edu.cn)
0 引言
直方图作为一种可以直观展示数据分布的统计工具,在社交网络分析、数据共享等领域有广泛的应用。数据采集者收集用户数据,汇总为直方图发布给第三方数据挖掘者,数据挖掘者从统计直方图挖掘有价值的知识,用于辅助决策。该过程中数据挖掘者为不可信角色,攻击者可以结合背景知识与统计直方图推断用户数据,导致用户隐私泄露问题。
差分隐私[1]作为数据隐藏发布常用技术之一,被广泛应用于直方图发布问题,已经提出的基于差分隐私直方图发布方法[2-16]可以分为数据无关(data-independent)方法与数据相关(data-dependent)方法。在隐匿过程中无需考虑原始数据分布的方法称为数据无关方法[2-4]。Hay 等[2]提出基于数据固有约束的约束推断方法,用于提高添加拉普拉斯噪声的直方图的可用性;Xiao 等[3]提出一种基于小波变换的直方图发布方法,首先对原始数据进行小波变换,基于变换后的数据添加拉普拉斯噪声。鉴于数据无关方法没有考虑直方图桶统计值的分布,无法获得具有较高可用性的发布直方图,由此引出数据相关的直方图发布方法研究。
数据相关研究代表性方法是基于分组的直方图发布方法[5-9]:一方面,分组操作将引入近似误差(Approximation Error,AE);另一方面,差分隐私所添加噪声会引入拉普拉斯误差(Laplace Error,LE)。该类方法通过平衡近似误差与拉普拉斯误差,在满足差分隐私的前提下发布与原始直方图尽可能相似的直方图。Acs 等[5]提出P-HPartition 算法,通过遍历所有候选分割点,选择误差最小值对应划分方案。Xu 等[6]提出NoiseFirst 与StructureFirst 方法,NoiseFirst 在原始直方图添加噪声后应用动态规划求得k 个最优分组;StructFirst 使用指数机制对原始直方图求得k 个最优分组,进而在组均值添加拉普拉斯噪声。P-HPartition、StructureFirst 与NoiseFirst 都是基于局部分组的思想,仅考虑局部范围内桶的数值近邻,无法度量全局计数的近邻关系,不能很好地平衡近似误差与拉普拉斯误差。
针对局部分组存在的不足,发展出基于全局分组的直方图发布方法。考虑到在原始直方图全局分组违背差分隐私约束[7],Kellaris 等[7]提出通过行采样或列采样的方法获得有序直方图,进而通过固定分组获取全局分组,该方法的缺陷在于固定分组不能较好地均衡近似误差与拉普拉斯误差,因此不能得到较高可用性的发布直方图。张啸剑等[8]利用马尔可夫链蒙特卡洛方法中的Metropolis-Hastings 方法与指数机制获得有序直方图,采用贪心聚类获得全局分组,但是采样方法具有随机性,无法保证排序正确性,贪心聚类也无法较好地均衡近似误差与拉普拉斯误差。Zhang 等[9]提出AHP(Accurate Histogram Publication)方法,对添加噪声的直方图排序并贪心聚类获得全局分组,发布直方图可用性受隐私预算参数影响较大,在隐私预算较小的情况下无法有效平衡近似误差与拉普拉斯误差。因此,已有全局分组的方法基于采样或对添加噪声的直方图处理无法获得可靠的有序直方图,并且通过固定分组或贪心聚类无法保证分组误差均衡,限制了发布直方图的可用性。
目前基于分组的直方图发布方法虽然可以保证发布直方图的隐私安全性,但是无法保证发布直方图的精度,导致低可用性。现有方法主要存在以下问题:
1)局部分组方法只能聚合位置近邻的桶,无法聚合全局范围内数值相近的桶,不能均衡近似误差与拉普拉斯误差,导致发布直方图精度较低。
2)全局分组方法通过对原始直方图采样或对添加噪声的直方图排序逼近基于统计数值排序的原始直方图的桶顺序,具有较大的随机性,无法保证发布直方图的可用性。
3)全局分组方法通过固定分组或贪心分组逼近原始直方图的最佳误差平衡全局分组,可能陷入局部最优,无法较好地均衡近似误差与拉普拉斯误差,导致发布直方图可用性降低。
针对上述问题,基于全局分组思想,采用约束推断方法对直方图排序,设计基于动态规划的分组方法,在添加噪声的直方图上实现最佳误差平衡的全局分组,进而提出基于全局分组的高精度直方图发布方法(High Precision Histogram Publishing,HPHP)。
本文主要贡献如下:
1)针对已有方法无法保证添加差分噪声的直方图与基于统计值排序的直方图具有相同的桶顺序,采用约束推断对添加有序约束的原始直方图修正实现直方图的排序。
2)提出基于动态规划的分组方法,在添加噪声的直方图上实现具有最佳误差平衡的全局分组,均衡近似误差与拉普拉斯误差,降低发布直方图与原始直方图的总体差异。
3)解析基于分组的方法可能达到的最佳误差平衡,提出理论最小误差Optimal 方法,并设计对比实验,验证所提方法的有效性。
1 问题描述及相关概念
1.1 问题描述
给定数据集D 存在属性A,D 中任意一条记录为t。发布者需要统计属性A 不同取值的记录数量,并整理为直方图发布。若A 是离散属性,每一个离散取值对应一个统计值;若A是连续值属性,首先对A 离散化,将A 的取值区间划分为若干个子区间,每一个取值区间对应一个统计值。对于两种类型的属性,直方图发布方法是相同的,为方便起见,本文只讨论A 是离散属性的情况。假设攻击者已经得知数据集除t 以外所有记录在属性A 上的取值,结合直方图,攻击者可以准确地推断元组t在属性A的取值,导致隐私泄露。
例 表1 是疾病与相应患者数量的统计表,医院需要将上述统计数据发布供分析人员应用。若共有340 人参与疾病统计,假如攻击者已经知道Alice 参与统计,并掌握其他患者的患病情况,可以准确地推断Alice所患疾病。
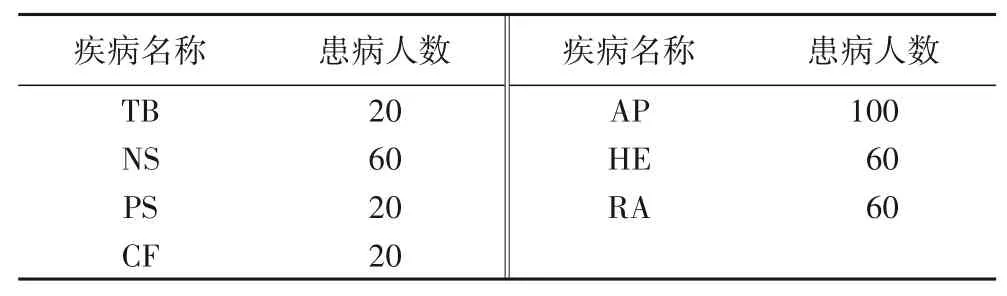
表1 患者统计表Tab.1 Patient statistics
1.2 相关概念
定义1直方图。假设数据集D 存在属性A,A 取值范围是V;对 于∀t ∈D,∀v ∈V,定 义Hi=count(t.A=v),其 中count(x)表示统计数据集D 中符合条件x 的记录数量。基于属性A 统计得到直方图H={H1,H2,…,Hn},其中n=|V|,Hi表示V中第i个属性取值的统计值。
定义2ε-差分隐私[1]。若数据集D 与D'仅有一条记录不同,那么称D 与D'为邻居数据集,对于D 与D',查询函数F满足差分隐私,当且仅当F满足:

其中Pr[F(D) ∈S]表示在D上执行F的结果在S中的概率。
定义3全局敏感度[1]。给定查询F:D →Rd与数据集D及其邻居数据集D',定义全局敏感度为:
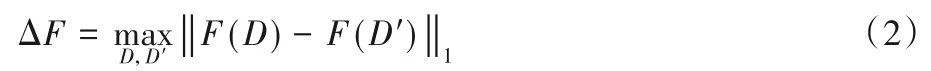
定义4拉普拉斯机制[1]。给定查询F:D →Rd,为了使F 满足差分隐私,需要在其查询结果上添加满足拉普拉斯分布的噪声。具体形式如下:

1.3 基本思路
图1 为HPHP 流程框图。HPHP 算法可以分为6 个步骤:①原始直方图排序,增加有序约束;②添加拉普拉斯噪声;③基于添加噪声的直方图,约束推断处理;④基于处理后的直方图,动态规划分组获得添加噪声的直方图上具有最佳误差平衡的分组⑤原始直方图根据分组,得到⑥基于每一个分组,组内统计值被替换为添加拉普拉斯噪声的组均值,进一步根据非负约束对添加噪声后的统计值修正,得到发布直方图

图1 HPHP流程框图Fig.1 Block diagram of HPHP process
2 基于差分隐私的高精度直方图发布方法
通过分析已有方法,得出以下3点结论:
1)相较于局部分组,全局分组能够更有效地均衡近似误差与拉普拉斯误差;
2)添加差分噪声的直方图与基于统计值排序的直方图具有相同的桶顺序,有利于全局分组;
3)在添加噪声的直方图上得到最佳误差平衡的分组,可以更好地平衡近似误差与拉普拉斯误差。
针对1),本文所提方法采用全局分组的思想。针对2),已有方法通过对原始直方图采样或者对添加噪声的直方图排序逼近基于桶计数排序后原始直方图的顺序,以上两种方法都带有较大的随机性,往往导致不准确的排序。针对该问题,本文首先对原始直方图增加有序约束,添加噪声后应用约束推断[2]方法对直方图修正,使添加噪声的直方图与基于桶计数排序的直方图桶顺序一致。针对3),由于不能直接对原始直方图全局分组,需要在采样序列或添加噪声的直方图上获得全局分组,根据分组将原始直方图划分。已有方法使用固定分组[7]或贪心聚类[8-9],无法使近似误差与拉普拉斯误差得到较好的均衡。针对该问题,本文提出自适应的动态规划分组算法,在添加噪声的直方图上得到具有最小总误差的全局分组。
基于上述分析,提出综合考虑3 个结论的直方图发布方法HPHP。该算法可以分为3个阶段:
1)间接排序阶段。针对直接对原始直方图排序分组导致无法满足差分隐私约束的问题,首先在原始直方图添加有序约束并添加拉普拉斯噪声,采用约束推断对添加噪声的直方图约束推断处理。
2)全局分组阶段。基于第1)阶段得到的有序直方图,采用基于动态规划的全局分组方法,获得分组方案。
3)发布阶段。基于前两阶段得到的分组方案,将原始直方图分组并添加差分隐私约束,得到发布直方图。结合直方图箱统计值本身具有的非负约束,进一步对发布直方图修正。
以下给出HPHP算法的3个阶段的详细分析。
2.1 约束推断
HPHP第1阶段为间接获得有序直方图,基于有序直方图分组,能够有效地降低近似误差,更好地平衡近似误差与拉普拉斯误差。第1 阶段通过对原始直方图排序并添加噪声得到满足差分隐私约束的直方图,基于添加噪声的直方图采用约束推断对直方图修正使其满足有序约束一致性。约束推断利用查询固有约束对添加噪声的数据修正,降低数据的噪声量,固有约束包括有序约束、非负约束等。若有序原始直方图为Hs,添加噪声之后为采用文献[2]的定理求解满足有序约束的解,定理描述如下:

例如,当Hs具有非降序约束,若根据定理1 得到约束推断详细描述见算法1[17]。
算法1 ConstrainedInference。

定理2HPHP第1阶段满足差分隐私与约束一致性。
证明 在原始直方图添加有序约束并添加服从Lap(1/ε1)的拉普拉斯噪声满足差分隐私。假设原始直方图H={H1,H2,…,Hn},添加有序约束后的直方图Hs={Hs1,Hs2,…,Hsn},H 与Hs的全局敏感度相同,因此添加的噪声均服从Lap(1/ε1)分布;假设H 与Hs添加噪声后得到的直方图为都满足ε1-差分隐私约束。由于排序发生于添加噪声之前,因此攻击者具有“查询结果是有序的”的背景知识,若结果中出现了乱序,可以断定查询结果添加了噪声,因此违背一致性。通过约束推断处理,可以使重新有序,保持添加噪声前后的有序一致性。 证毕。
2.2 动态规划分组
HPHP 第2 阶段为间接获得分组方案。为了均衡近似误差与拉普拉斯误差,需要自适应地将添加噪声的直方图分组,使得所有分组的总误差达到最小,总误差由近似误差与拉普拉斯误差两部分构成。为了定义分组误差,首先给出原始直方图与发布直方图的误差计算方法,定义如下:
定义5发布直方图的误差[8]。假设原始直方图为H,发布直方图为E(⋅)表示期望值。定义二者之间的误差为:

式(4)通过计算原始直方图与发布直方图桶统计值的均方差之和得到发布直方图的误差,作为发布直方图的一个子集,分组误差也使用均方差公式计算,分组误差
定理3[8]对于任意分组其具有误差是分组的均值,是分组的近似误差,是分组的拉普拉斯误差。
HPHP 第2 阶段基于约束推断处理后的有序直方图自适应获得总误差最小的全局分组方案,该问题适合使用动态规划解决,问题描述如下:对于数组寻找若干分割点,使得分割后所有分组的总误差最小,分组的误差评价函数动态规划解决方法的递推公式给出如下:
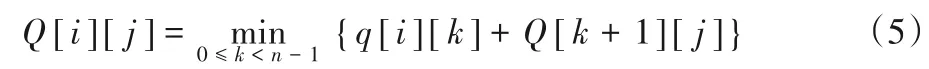
动态规划分组方法DPCluster 时间复杂度分析。DPCluster 首先需要求解q矩阵,若使用公式计算,时间复杂度为O(n3),因此修改此时求解q 矩阵的时间复杂度降为O(n2)。得到q 矩阵之后,求解Q 矩阵,该过程时间复杂度为O(n2)。因此动态规划分组算法的时间复杂度为O(n2)。
2.3 HPHP算法
基于前面两节分析,可以在满足差分隐私约束前提下间接获得原始直方图的全局分组方案。HPHP 第3 阶段基于分组方案将原始直方图分组,将分组中的统计值用组均值替换并分别添加拉普拉斯噪声,得到发布直方图。为了进一步满足非负约束,提升发布直方图的可用性,需要将发布直方图中负值统计值替换为0。经过HPHP三个阶段的处理,可以得到满足差分隐私的发布直方图。
基于3 个阶段的算法设计,可以在满足差分隐私与一致性约束前提下获得较高可用性的发布直方图,进一步提出HPHP算法,详细描述见算法2。
算法2 HPHP。
输入 原始直方图H={H1,H2,…,Hn},隐私预算ε;

HPHP算法的3个阶段对应如下:1)原始直方图添加有序约束(第2)行),添加拉普拉斯噪声(第3)行),对添加噪声的直方图约束推断处理(第4)行);该阶段在满足差分隐私与一致性约束前提下间接得到有序直方图;2)基于处理后的直方图,动态规划分组获得分组(第5)行);通过在有序直方图动态规划得到的分组方案,比较接近直接在原始直方图全局分组的分组结果;3)原始直方图根据分组方案划分(第6)行),统计值被添加拉普拉斯噪声的组均值代替(第7)~10)行),非负约束处理(第11)行),得到发布直方图;第3 阶段得到发布直方图,同时维护直方图的非负约束一致性。
定理4HPHP算法满足一致性约束。
证明 定理2 已经证明HPHP 第1 阶段满足有序约束一致性;HPHP 第2 阶段只涉及分组操作,因此不需要维护一致性;第3 阶段通过非负约束将发布直方图负统计值修正,满足非负约束一致性。因此HPHP算法满足一致性约束。证毕。
定理5HPHP算法满足(ε1+ε2)-差分隐私。
证明 HPHP 算法满足差分隐私约束。隐私安全性评价需要从ε-差分隐私的定义分析,结合算法2 的具体步骤,分析每一步是否存在隐私泄露。根据定理2 可知,算法2 的1)~4)行满足差分隐私;5)~7)行为访问原始直方图;8)~10)行在组均值添加服从Lap(1/ε2)分布的拉普拉斯噪声,满足差分隐私;11)行非负约束处理的是添加噪声后的发布直方图,满足差分隐私。综上所述,HPHP满足差分隐私。
算法2分别在第3)行与第10)行添加了拉普拉斯噪声,两次都是在原始直方图添加噪声,根据定理6,可以知道HPHP满足(ε1+ε2)-差分隐私。 证毕。
定理6[8]设有一系列算法M1,M2,…,Mk分别满足隐私保护预算为ε1,ε2,…,εk的差分隐私,若k 个算法作用于同一数据集D,则组合算法M(M1(D),M2(D),…,Mk(D)) 满 足差分隐私。
2.4 理论最小误差直方图发布算法
通过分析基于分组的直方图发布方法可能达到的最佳误差均衡,设计了获得理论最小误差直方图的Optimal算法。文献[7]指出,在原始直方图全局分组不能满足差分隐私约束,直方图H 与其邻居H'相差一条记录,二者的全局分组无法保持一致,无法满足式(1),因此后续的工作都致力于间接获得原始直方图的全局分组。文献[7]与文献[8]使用采样与贪心聚类近似原始直方图全局分组,文献[9]通过对添加噪声的直方图分组近似原始直方图全局分组,本文所提方法同样通过对添加噪声的直方图处理近似原始直方图的全局分组。以上方法中,近似得到的全局分组与原始直方图全局分组的相似度决定是否能够合理平衡近似误差与拉普拉斯误差,进而决定发布直方图的可用性。因此,在原始直方图上排序并动态规划分组,可以使近似误差与拉普拉斯误差达到最佳平衡,得到理论最小误差直方图。
基于以上分析,提出可以获得理论最小误差直方图的Optimal 方法,方便与已有方法对比分析。需要说明,Optimal违反了差分隐私的定义,因此无法得到可发布的直方图。Optimal方法详细描述见算法3。
算法3 Optimal。
输入 原始直方图H={H1,H2,…,Hn},隐私预算ε2;

定理7Optimal方法得到的发布直方图精度是已有基于全局分组的直方图发布方法的上界。
证明 基于全局分组的直方图发布方法可以分为3 个阶段:间接对直方图排序,得到与基于统计值排序的原始直方图相近的有序直方图;基于有序直方图,间接获得与基于原始直方图全局分组相近的分组方案;将原始直方图分组,添加拉普拉斯噪声发布。Optimal方法在第1阶段直接对原始直方图排序,相较于已有方法间接获得有序直方图,Optimal 方法得到的有序直方图桶统计值次序更加准确;Optimal 方法在第2 阶段直接对有序直方图动态规划分组,相较于已有方法在采样序列或添加噪声的直方图上间接获得分组方案,Optimal 方法可以得到原始直方图上具有最佳误差平衡的分组方案。综上,可以推断Optimal方法得到的发布直方图精度是已有方法的上界。 证毕。
3 实验分析
实验所用硬件环境为Intel Core i5CPU 2.40 GHz,4 GB 内存,操作系统平台为Windows10操作系统,使用Java 编程语言与C++语言实现所有方法,给出HPHP 算法与理论最小误差算法(Optimal)、直接添加噪声的DP 算法[1]、AHP 算法[9]的实验对比结果。
实验采用相对熵(Kullback-Leibler Divergence,KLD)与均方误差的自然对数(Natural Logarithm of Mean Square Error,LNMSE)作为评价标准,详细定义见3.1节。
实验采用直方图发布经常使用的4 个数据集,分别是waitakere[9]、search_log[2]、nettrace[2]和socialnetwork[2]。其中:waitakere 是从新西兰2006 年人口街区普查数据中抽取7 725个街区的数据构成的统计直方图,街区人口数量作为直方图的桶;search_log 由Google Trends 与American Online 的搜索数据合并而成,每个桶包含90 min 搜索“Obama”次数的统计值;nettrace 源自一所高校的路由追踪数据统计;socialnetwork 来自一个在线社交网站的关系统计。数据集的详细信息见表2。

表2 数据集信息Tab.2 Dataset information
设置不同的隐私预算,分别比较四个算法在不同数据集的KLD 与LNMSE。在相同的实验预置条件下,直方图误差越小说明发布直方图与原始直方图差异越小,发布直方图精度越高。理论上,Optimal 算法发布直方图误差最小,而直接加噪声的DP 算法发布直方图误差最大,HPHP 算法和AHP 算法发布直方图的误差介于Optimal算法与DP算法之间。
3.1 发布直方图误差评价标准
本节给出评价发布直方图与原始直方图之间差异的标准:KLD 与LNMSE。发布直方图与原始直方图的KLD 与LNMSE 越小,发布直方图与原始直方图的差异就越小,发布直方图的精度与可用性越高。
KLD评价两个直方图之间的分布差异。计算原始直方图H与发布直方图之间的相对熵,公式给出如下:
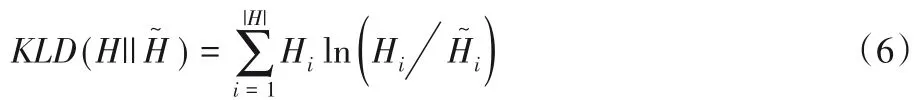
LNMSE 即均方差的自然对数。均方差评价发布直方图桶统计值偏离原始直方图统计数值的程度,使用自然对数可以降低均方差数量级,便于观察实验结果。给定一组统计查询Q={Q1,Q2,…,Ql},原始直方图H与发布直方图的LNMSE计算公式给出如下:
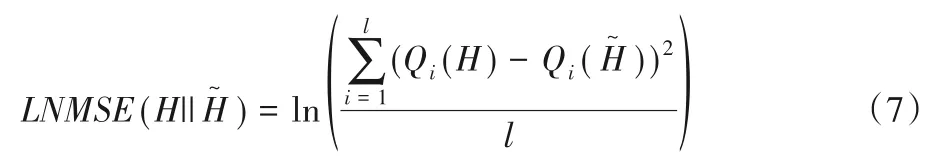
3.2 KLD对比实验
图2是Optimal、HPHP、AHP 与DP 分别在4个数据集运行得到的KLD对比,分别设置隐私预算ε=0.01、0.1、1.0。
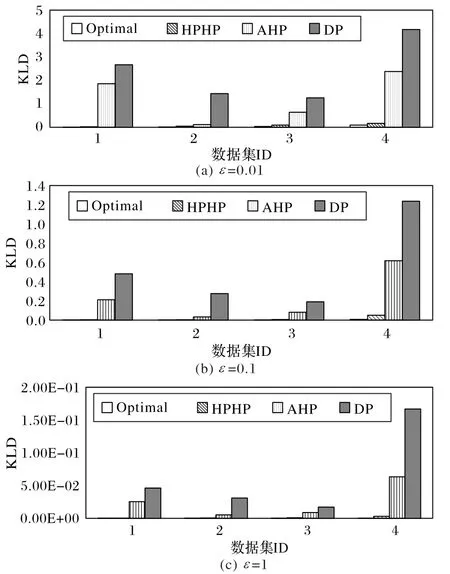
图2 不同隐私预算下的KLD对比Fig.2 KLD comparison with different privacy budgets
从图2 中可以看出,HPHP 算法发布直方图的KLD 值与Optimal 算法发布直方图的KLD 值较为接近。相较于直接在统计数添加噪声的DP,AHP 基于添加噪声直方图分组,并使用贪心方法平衡近似误差与拉普拉斯误差,显著降低了误差。与AHP 不同的是,HPHP 保证添加噪声的直方图与直接基于桶计数排序的直方图具有一致顺序,即使处理比较特殊的直方图,也能获得较好的全局分组,使近似误差与拉普拉斯误差得到较好均衡,进而得到误差较小的发布直方图,在不同的隐私预算与数据集条件下,HPHP 所发布直方图的KLD 误差约为AHP的10%。
不同于其他数据集,nettrace(ID 为2)是有序数据集,Optimal、HPHP与AHP均获得了较高精度的发布直方图,说明分组前数组的有序程度越高,基于分组的直方图发布方法越能有效均衡近似误差与拉普拉斯误差,进而获得误差较小的发布直方图。
3.3 LNMSE对比实验
设置实验数据集waitakere,图3 给出Optimal、HPHP 与AHP 在隐私预算ε=0.01、0.1、1.0 时,查询范围为{50,100,150,200,250,300,350,400,450}的LNMSE 对比。随着查询范围逐渐增大,噪声逐渐累积,误差呈递增趋势。在隐私预算较小时,AHP 的对数均方差远大于HPHP 与Optimal,HPHP 的对数均方差接近Optimal,保证发布直方图的高可用性;随着隐私预算增大,三个算法发布直方图的误差都在降低,并且呈逐渐接近趋势。因此,隐私预算充足时,AHP 与HPHP 发布直方图的差异较小,隐私预算较小时,HPHP 算法能获得更低LNMSE的发布直方图。

图3 不同隐私预算下的LNMSE对比Fig.3 LNMSE comparison with different privacy budgets
4 结语
针对满足差分隐私的直方图发布问题,本文首先分析已有基于分组的差分隐私直方图发布方法存在的缺陷,并在此基础上提出HPHP 算法;使用约束推断,使添加差分噪声的直方图与基于桶计数排序的直方图具有相同顺序,同时提高直方图的精度;基于有序直方图提出动态规划分组方法,在添加噪声的直方图上获得具有最小误差的分组。通过分析基于分组的方法可能达到最佳误差均衡,提出理论最小误差Optimal方法。HPHP 与Optimal、AHP 在真实数据集上的实验对比结果表明:HPHP 发布直方图误差小于已有算法,接近Optimal的理论最小误差。当隐私预算较小时,约束推断后的直方图可能具有大量相同的统计值,未来工作考虑解决这一问题,得到更加接近理论最佳误差均衡的分组,进一步提升直方图发布精度。

