基于离散灰狼算法的喷涂机器人路径规划方法

梅 伟，赵云涛，毛雪松，李维刚

（冶金自动化与检测技术教育部工程研究中心（武汉科技大学），武汉 430081）

（∗通信作者电子邮箱1739710730@qq.com）

0 引言

机器人在喷涂领域的应用，不仅解放了人工，而且通过提高喷涂质量和效率极大地提高了产品竞争力。随着喷涂机器人运用到更多行业，产品结构变得复杂多样，对机器人自动喷涂技术提出了更高的要求。路径规划作为机器人自动喷涂技术的关键步骤，决定了涂层的厚度和均匀性、完成喷涂工作的时间、机器人在工作空间的运动过程等。因此，研究喷涂机器人的路径规划方法对于提高喷涂质量和效率、降低成本、提高安全性等具有重要意义。

对于表面结构类型单一的物体，直接采用基于切片技术或轮廓线连续偏置的方法就能规划出满足要求的路径。文献［1］运用高斯博纳定理来选择最优起始线和偏置线规划喷涂路径，从而提高了涂层均匀性和喷涂效率；文献［2-3］则分别给出了自由曲面、平面、柱面、锥面和球面等常见类型的曲面路径规划方法，但对于表面结构复杂多样的物体，需要对每个区域进行路径规划，然后将区域间路径规划问题简化成广义旅行商问题（Generalized Traveling Salesman Problem，GTSP），最后运用智能算法规划全局路径；文献［4-5］为了提高蚁群优化（Ant Colony Optimization，ACO）算法求解该问题的速度和精度，将蚁群算法改进后运用到了其中的区域间路径规划问题；文献［6-7］将粒子群优化（Particle Swarm Optimization，PSO）算法改进为离散粒子群算法，并运用到该问题，规划了最短区域间过渡路径；文献［8］则考虑到多种算法可以求解该问题，分别运用遗传算法（Genetic Algorithm，GA）、粒子群算法和蚁群算法求解了区域间路径规划问题，结果显示粒子群算法求解的路径最短。上述方法有效提高了喷涂质量和效率，但将区域内路径规划问题与区域间路径规划问题分开考虑，规划的路径仍有不足：1）路径仍较长，效率低；2）路径存在碰撞且不平滑；3）三维到二维的坐标映射不适用于复杂结构实体；4）未考虑机器人能耗。本文不同于目前的研究仅考虑区域路径连接顺序，还要将每个区域内路径规划的多个决策变量考虑进来以解决这些问题，因此具有显著的多层决策特性，目前的方法都不适用。

灰狼算法是Mirjalili 等［9］在2014 年基于灰狼群体捕食行为提出的一种新的智能算法，由于其卓越的性能，在机器学习［10］、工业控制［11］等领域得到了较好的应用。目前将灰狼算法改进为离散域的灰狼算法的探索也有很多，文献［12］与文献［13］提出将离散灰狼算法运用于车辆路径问题和旅行商问题（Traveling Salesman Problem，TSP），但两者均属于常规离散域问题，只能求解仅有顺序类决策变量的问题，且未考虑原始算法平衡全局性能和局部性能的策略，没有发挥灰狼算法的特性，因此不适用于多层决策GTSP。文献［14］则采用两段式编码方式解决了多决策层GTSP的编码问题，但当决策层和决策变量增多时，过长的向量难以表示序列类决策变量与其配置决策变量的对应关系，不易算子操作，而且还需要通过复杂的转换机制将实数编码转换为离散值，影响算法效率。

本文重新定义编码方式、初始化方式和种群更新策略，提出一种用于求解多层决策问题的离散灰狼算法（Discrete Grey Wolf Optimizer for Multilayer Decision Problem，MDPDGWO）。在运用该算法规划路径时，首先运用图论建立简化模型；然后，建立碰撞问题的数学模型作为约束条件，建立路径长度的数学模型作为目标函数；最后，利用该算法求解满足避碰约束和路径最短目标的最优区域间连接顺序、区域内路径规划切片方向、区域内路径连接顺序和区域内路径起止点选择，从而规划路径，且其中运用圆弧过渡提高路径的平滑性。

1 求解多层决策问题的离散灰狼算法

1.1 基本灰狼算法

灰狼算法［9］是基于灰狼群体捕食行为提出的一种新的智能算法，灰狼种群中存在等级制度和分工制度。适应度评价最好的前三头狼分别命名为α、β、δ，其余命名为ω。ω 狼在α、β 和δ 狼的带领下搜索猎物，其狩猎过程主要为以下3 个步骤：

1）包围。当狼群发现猎物时，通过式（1）包围猎物。

其中：t 为当前迭代次数，Xp为猎物位置，|C ⋅Xp(t)-X(t)|为当前狼位置X(t)与猎物位置Xp的距离，A与C为系数向量，分别由式（2）与式（3）计算得来：

其中：r1、r2为［0，1］范围内的随机向量，a 的每个分量随着迭代次数的增加由2线性递减到0。

2）捕猎。当狼群包围猎物时，狼群根据式（4）～（7）更新位置实施捕猎行为，且由3只头狼引导。

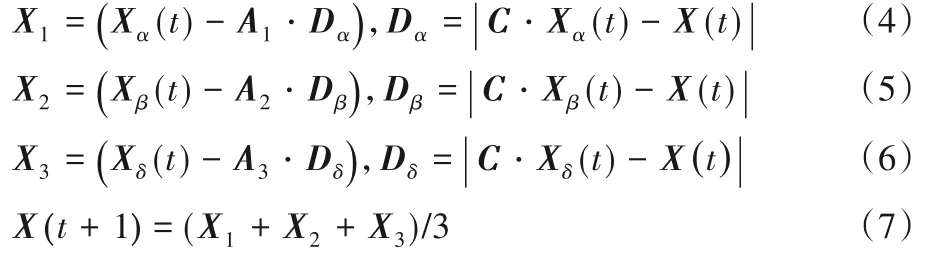
其中：Xα(t)、Xβ(t)、Xδ(t)为三只头狼的当前位置；Dα、Dβ、Dδ为三只头狼与其对应猎物的距离；X(t)为当前灰狼的位置；X(t+1)为当前狼更新后的位置。

3）攻击。攻击猎物完成狩猎。在算法前期，|A|＞1，狼群相对分散，进行全局搜索，找到猎物所在区域；随着a 的每个分量递减，|A|≤1，算法进入局部搜索阶段，狼群攻击猎物，找到最优解。

1.2 求解多层决策GTSP的矩阵编码方法

求解多层决策GTSP 时，每个节点具有多种配置，即节点具有随配置决策的不同而变化的权重。因此，提出一种矩阵编码方式，顺序（序列）类型决策层和具有多种选择的决策层仍采用整数编码，如节点顺序部分的决策层和每个节点具有多个配置选择的决策层，而仅具有两种选择的决策层采用二进制编码，最后组合成矩阵编码。如图1，共有6个节点，编号为1～6，第一行为节点顺序决策层，节点所在的列数即为该节点的顺序；第二、三行为节点多选择决策层，共有3 种可选配置，则用1～3编码；第四、五行为双选择决策层，用0和1编码，最终编码为如式（8）的矩阵形式。这种矩阵编码方式与实际问题的决策映射关系简单，每个节点与其配置决策变量对应关系很直观，易于编解码，也易于算法算子的计算。

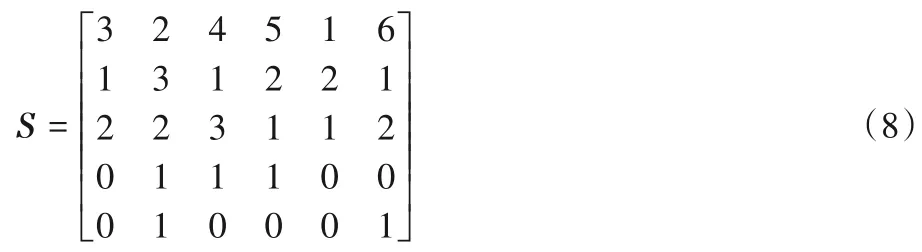
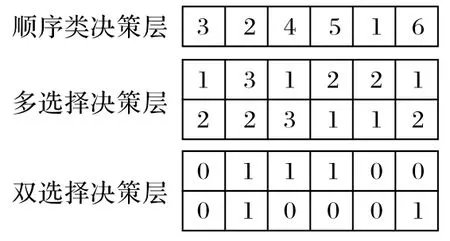
图1 矩阵编码方法示意图Fig.1 Schematic diagram of matrix coding method

1.3 基于先验知识和随机选择的混合初始化方法

不同于多数连续域优化问题具有太强的盲目性，求解GTSP得到的最优解往往是一定邻域内的节点连接在一起，且每个节点的配置选择也具有一定的经验认识。因此，考虑加入一定比例的基于先验知识的初始解，避免算法前期盲目搜索消耗时间，也给后期局部搜索提供很多优质片段，当然，仍保留一定比例的随机选择是为了保证初始种群的多样性，防止过早陷入局部最优。

在利用先验知识初始化时，非序列类决策以较大概率选择经验值即可，节点序列部分的初始化可以使用k 邻域（k 为较小的正整数）随机选择。如图2，首个节点（编号为3 的节点）通过随机选择得到，之后每次选择下一个节点，都通过在距离该节点（如编号为9的节点）最近的k个节点（k=3，编号为2、7、8的节点）中随机选择一个，直到所有节点都被选择。

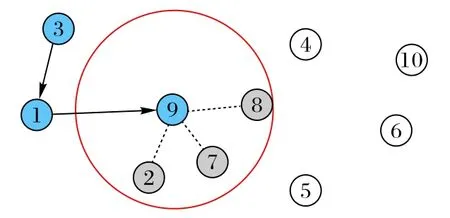
图2 k邻域初始化方法示意图Fig.2 Schematic diagram of k neighborhood initialization method

1.4 种群更新策略的离散化

在连续域的灰狼算法中，算法根据式（2）～（6）求当前灰狼与三只头狼的欧氏距离，然后根据式（7）更新当前灰狼的位置，其中参数A 和C 用于平衡算法的勘探能力和开发能力，参数A 的递减保证前期有较强的勘探能力，后期有较强的开发能力；参数C的随机性保证算法始终维持一定的种群多样性。因此，本文借鉴遗传算法中的交叉变异算子来重新定义灰狼算法的种群更新策略，同时保留原算法对勘探能力和开发能力的平衡策略。

定义如图3 的产生新解的交叉算子与两级变异算子。如图3（a），交叉算子为使用头狼中的优质片段替代当前灰狼的片段，且片段中节点的对应配置的决策变量跟随其进行交叉，片段的起止点随机产生，重复元素通过交叉片段中的对应关系消除。如图3（b），一级变异算子为当前灰狼两元素交换位置，且片段中节点的对应配置的决策变量跟随其进行交换，两元素位置随机产生。如图3（c），二级变异算子为当前灰狼除去序列决策层的决策变量更新算子，即任取几个元素替换成取值范围内的其他值，如二进制部分直接取反。

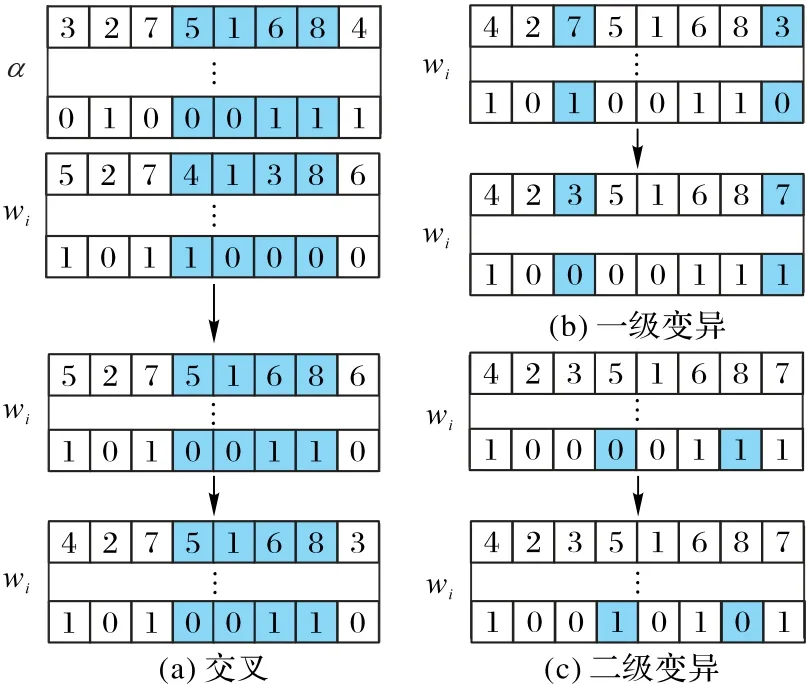
图3 种群更新算子示意图Fig.3 Schematic diagram of population update operators

另外，定义式（9）的新解接受度θ 概念，并设定接受度阈值参数θthreshold遵循式（10）的变化规律，当新解接受度满足θ ≥θthreshold时，接受使用产生的新解更新当前灰狼位置，该策略使得算法随着迭代过程不断降低对劣解的接受程度，平衡算法前后期的勘探能力和开发能力。

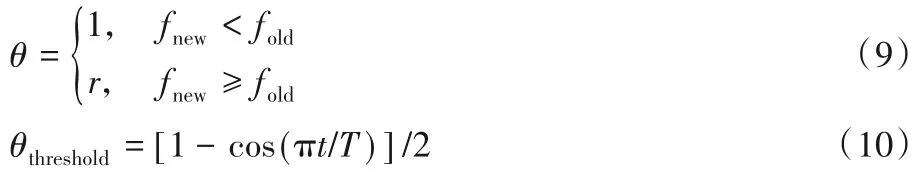
其中：r 为［0，1］范围内的随机数，t 为当期迭代次数，T 为迭代总次数。

1.5 MDP-DGWO算法

本文提出的求解多层决策问题的离散灰狼算法（MDPDGWO）伪代码如下：

算法 MDP-DGWO。

2 基于MDP-DGWO 算法的喷涂机器人全局路径规划方法

2.1 问题分析与建模

复杂结构实体的喷涂路径规划方法关键步骤如图4（a），其中区域内路径规划过程涉及多次决策，如切片方向可以选择横向或者纵向，每个区域最终会出现8 种路径结果。目前所有的方法均将区域内路径规划与区域间路径规划独立考虑，但实际上，区域内路径规划会产生多种结果，其选择的结果和区域间连接顺序同样会影响最终的路径长度等。本文将后两个步骤联合考虑规划全局路径，将区域间连接顺序、区域内切片方向、路径连接顺序和起止点的选择均纳入决策变量，所有过渡路径均采用圆弧过渡，并将区域间过渡路径与实体不能产生碰撞作为约束，规划最短路径。

如图4（b），将该问题简化为节点具有多种配置的GTSP问题，采用图论建立简化模型。假设被喷涂实体有n 个区域，每个区域有m 种可选路径配置，将每个区域定义为赋权图G中的节点V（vertex），则每个节点具有m 种权重ωv（该区域实际路径长度），将区域间过渡路径定义为赋权图中的边E（edge），则每两个节点连接的边具有m2种权重ωe，其大小取决于两个节点所选择的路径配置的起止点坐标，因此，赋权图G=（V，E，ωv，ωe），问题简化为求解在赋权图G中的一条非闭合通路，使得权重之和最小，且该非闭合通路由所有节点连接顺序和每个节点选择的路径配置表示。

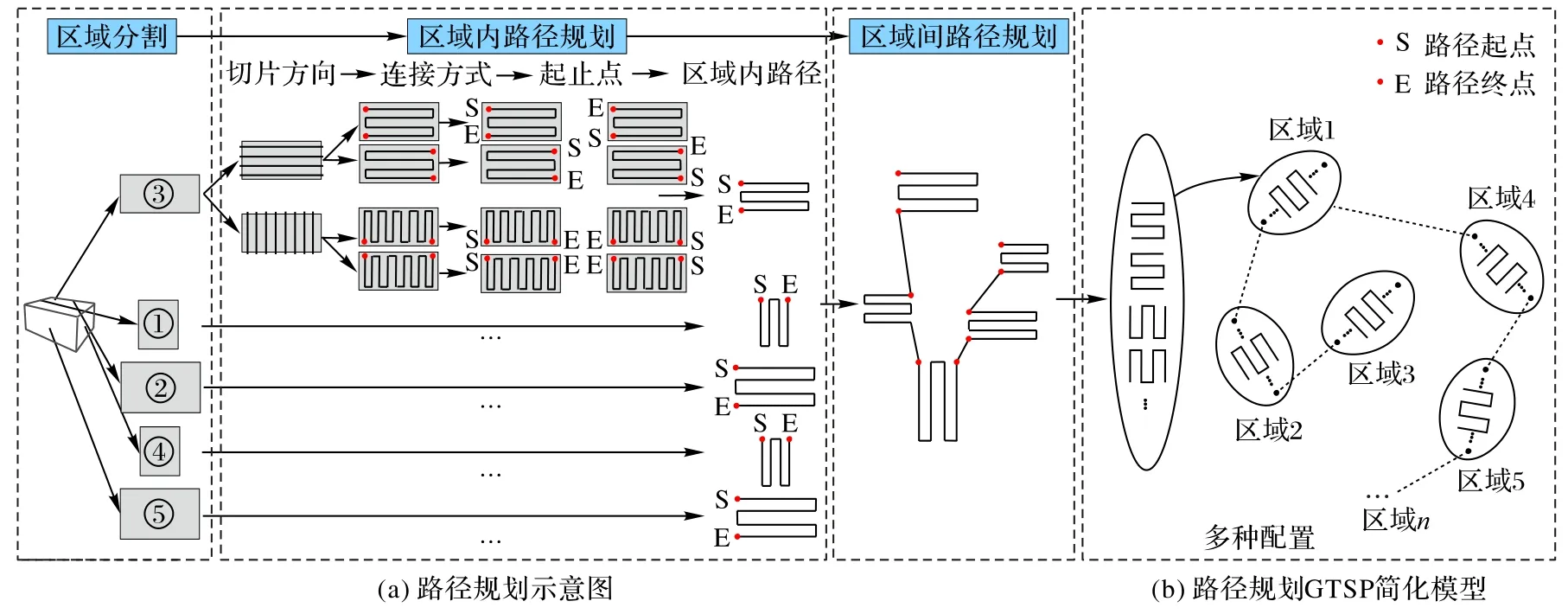
图4 路径规划问题示意图Fig.4 Schematic diagram of path planning problem

2.2 路径长度模型

为了提高喷涂过程的效率，则要求喷涂路径的长度尽可能短，而喷涂路径的长度主要包含n 个区域内的路径长度ωv和n -1条区域间过渡路径的长度ωe，建立如下路径长度的优化目标函数：

2.3 路径碰撞模型

复杂结构实体的喷涂路径在规划时要考虑到区域间过渡路径与被喷涂实体的碰撞问题，即路径要与被喷涂实体保持一定的安全距离dsafe。本文被喷涂实体模型为三维点云数据，即一个表示该物体轮廓的点集PC，对于任一过渡路径线段AB，其满足不存在碰撞约束的充分条件为：对于∀P ∈PC，都有点P到线段AB的最短距离d ＞dsafe。为了减少计算量，本文首先采用点云库（Point Cloud Library，PCL）中的体素化下采样［15］将点云数据精简为数据量小且均匀的点集，然后对每一条过渡路径进行碰撞检测时先滤掉PC 中不满足如式（12）～（14）条件的点，最后根据式（15）判断是否碰撞。

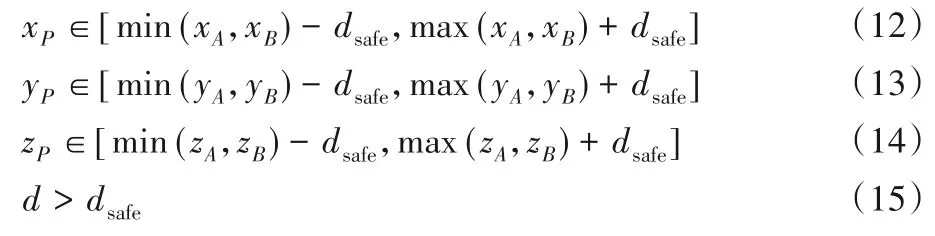
3 实验与结果分析

为了选择最优初始化比例因子r，从而充分发挥混合初始化策略对MDP-DGWO算法性能提升的作用，以及验证用于规划喷涂机器人全局路径的MDP-DGWO 算法是否解决了目前的研究所未考虑到的问题，以如图5 所示的实体曲面点云模型设计实验。

3.1 最优初始化比例因子选择实验

启发式算法的初始解往往很大程度影响算法的速度和精度，选取最优比例因子才能保证算法初始解的质量。为此，本文以0.1为步长，从0.0～1.0调节算法初始化比例因子r，并在对应参数下重复20 次路径规划实验，记录并统计算法收敛时的路径长度和迭代次数，得到表1 的统计数据，并将在各项统计值中表现较好的若干项标粗。

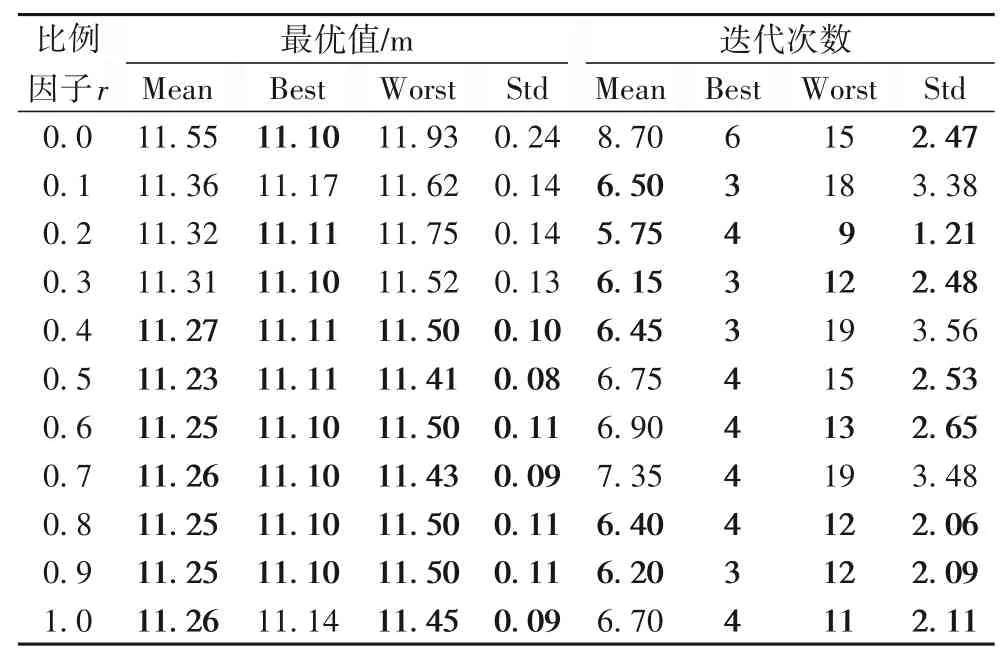
表1 不同比例因子下路径规划的结果比较Tab.1 Comparison of path planning results under different scaling factors

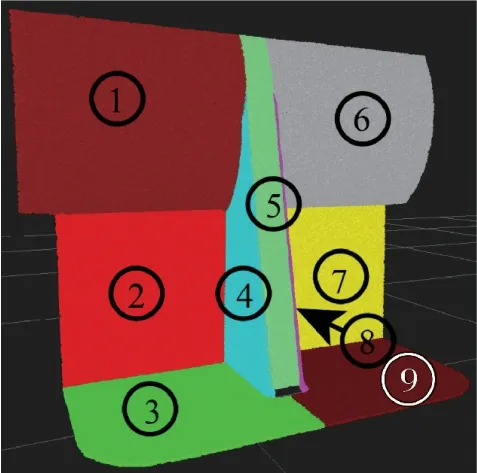
图5 实体曲面点云模型Fig.5 Point cloud model of entity surface

表1 中，算法在比例因子达到一定水平（r≥0.4）时比在较低的比例因子（0≤r＜0.4）下最优值整体表现更好；算法在比例因子达到一定水平（r≥0.3，除r=0.7）时比在较低的比例因子（0≤r＜0.3）下收敛需要的迭代次数更少；比例因子在为0.6、0.8、0.9 时算法整体性能表现最好。因此，加入一定比例的基于先验知识的初始解后，给算法求解提供了较多的优质片段，避免了算法搜索时的盲目性，使得算法能够更快求解出更优的解，保留一定比例的随机选择的初始解，能够保证初始种群的多样性，避免陷入局部最优。

3.2 算法对比实验与分析

为了验证路径碰撞、过渡路径较长导致效率不高，路径不平滑等问题是否解决，设计如下实验。分别用比例因子为0.8 的MDP-DGWO 算法、PSO 算法［6-7］、GA［8］和ACO 算法［4-5］重复20 次路径规划实验，记录并统计算法收敛时的路径长度、迭代次数和路径碰撞次数，得到表2 的数据。为了进一步分析算法表现出的动态性能，以及规划的路径实际情况，绘制如图6 的各算法迭代过程中的路径长度变化曲线和图7 中各算法实际规划出的路径。

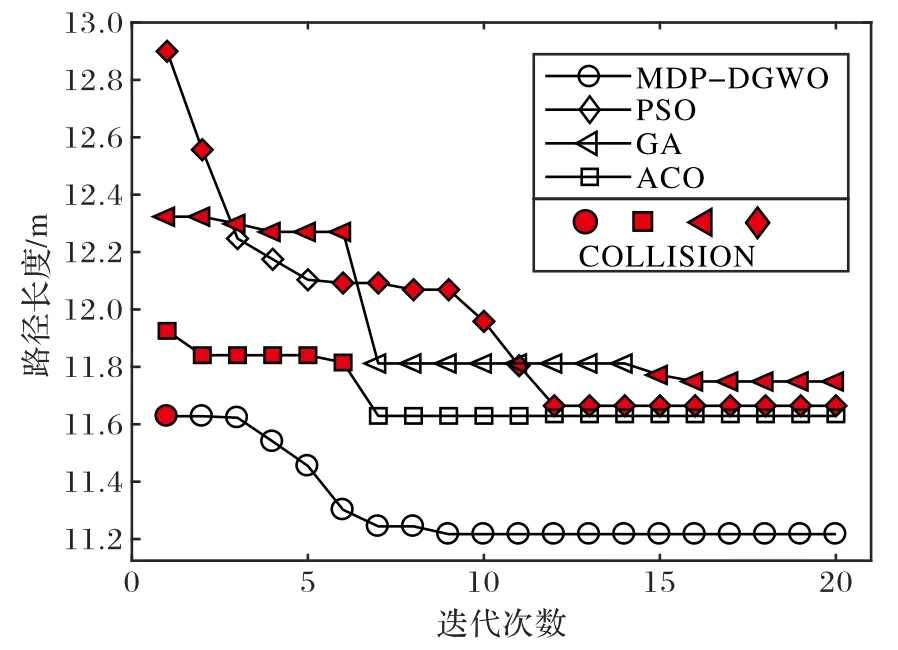
图6 路径长度变化曲线Fig.6 Change curves of path length

比较表2 中的路径长度的最优值数据，20 次实验中PSO、GA 和ACO 求解得到的路径长度波动幅度分别为0.6 m、0.48 m、0.68 m，而MDP-DGWO 求解得到的路径长度波动幅度仅为0.4 m，且MDP-DGWO比其他三种算法的标准差都小，MDP-DGWO 更为稳定。主要是因为启发式优化算法的鲁棒性不仅取决于算法的种群更新策略，而且受初始解的质量影响很大，本文除了引入新解接受度概念来平衡算法的勘探与开发能力，还提出了通过在初始解中加入基于先验知识的解以提高初始解的质量，从而提高了算法的鲁棒性。20 次实验中PSO、GA 和ACO 求解得到的最短路径长度为11.63 m，而MDP-DGWO 求解得到的最短路径长度仅为11.10 m，因此，MDP-DGWO 算法的多层决策策略考虑到了区域内路径规划结果对全局路径规划的影响，使得规划的全局路径长度突破了11.63 m 的限制，使得可能达到的最短路径减小为11.10 m。20 次实验中PSO、GA 和ACO 求解得到的路径长度平均值分别为11.84 m、11.90 m、12.04 m，而MDP-DGWO 求解得到的路径长度平均值仅为11.25 m，相对于其他三种算法路径长度分别减小了5.0%、5.5%和6.6%，长度明显减小，证明了算法采用的多层决策策略、混合初始化策略以及新的种群更新策略明显提高了算法的求解性能，对于提高喷涂效率具有显著效果。比较表2 中求解迭代次数数据，MDPDGWO 算法求解过程迭代次数相对少很多，证明了混合初始化等策略加速了算法的求解过程。比较表2 中碰撞次数数据，在20 次全局路径规划实验中，PSO、GA、ACO 算法超过10次实验规划的路径存在碰撞，路径不可用，而MDP-DGWO 因为建立了碰撞模型，存在碰撞的解会因为适应度较差，不会被选择为头狼，完全避免了碰撞的可能性。

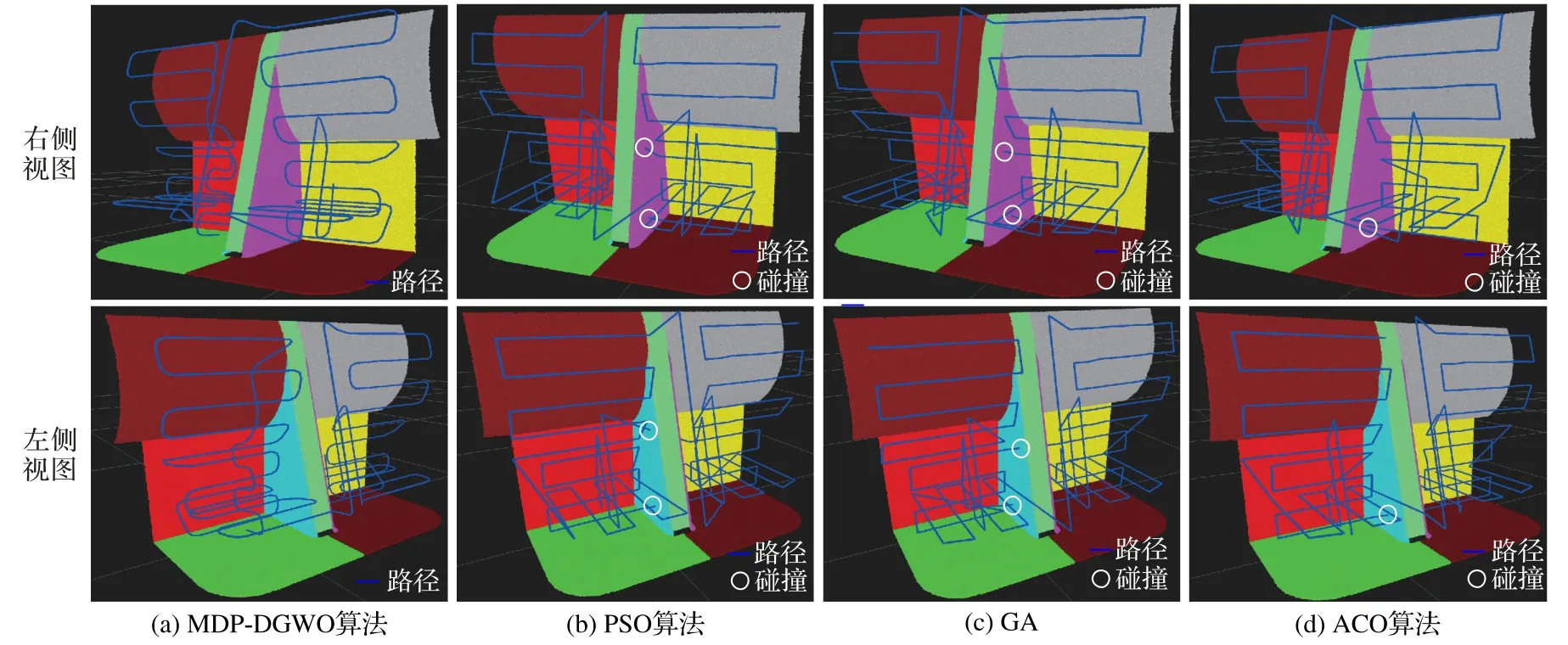
图7 四种算法规划的路径结果比较Fig.7 Comparison of path planning results of four algorithms

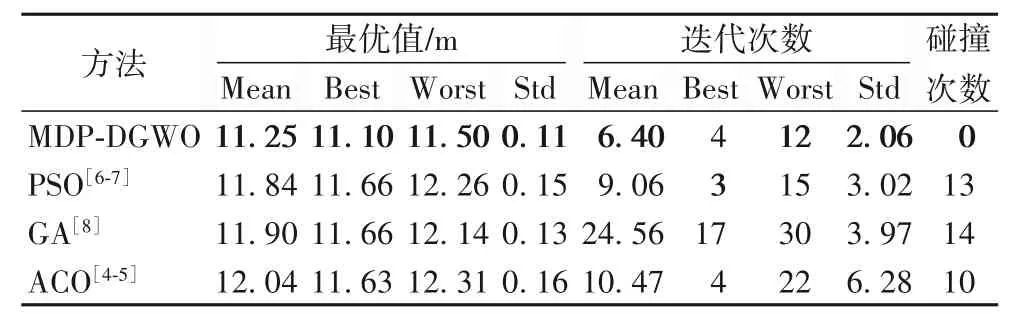
表2 四种算法路径规划结果比较Tab.2 Comparison of path planning results of four algorithms

图6 中，MDP-DGWO 算法在初始化时已存在了与其他三种算法最终求解得到的最优值相近的解，很明显避免了算法初期搜索的盲目性，而且由于碰撞模型，MDP-DGWO 算法很快就将具有碰撞的路径转化为无碰撞路径，其他算法则因为仅考虑路径更短而出现了穿越实体模型的路径，引起碰撞。

从图7 的中各算法规划的实际路径可以看出，MDPDGWO规划的路径更平滑、有序且没有碰撞，而其他三种算法规划的路径存在碰撞、转弯陡峭与路径杂乱等情况，不适用于实际情况，证明了MDP-DGWO规划的喷涂路径具有更强的安全性和适用性。

4 结语

本文提出一种用于解决多层决策问题的离散灰狼算法，并运用提出的算法规划喷涂机器人全局路径，得到如下结论：

1）对于解决GTSP的算法，在初始化时加入一定比例的基于先验知识的初始解能够提高算法求解精度和效率，本文提出的MDP-DGWO 算法在初始化比例因子为相对较高的水平（0.6、0.8、0.9）时能表现出较好的性能；

2）对于喷涂机器人路径规划问题，将区域内路径规划与区域间路径规划问题联合考虑，可以规划出更优的路径，本文提出的MDP-DGWO算法相对于目前的算法，规划出的路径效率更高、过渡更平滑且与被喷涂实体没有碰撞。

本文未从机器人角度深入考虑，将机器人在路径上的能耗问题考虑在内能够降低成本，下一步将考虑基于机器人逆运动学建立能耗模型，并将算法改进为多目标优化算法，用于求解能耗最优与路径最短的多目标优化问题。