面向空气质量的时空混合预测模型

黄伟建，李丹阳，黄 远

（河北工程大学信息与电气工程学院，河北邯郸 056038）

（∗通信作者电子邮箱757918272@qq.com）

0 引言

由于气候变化、工业生产和人口聚集等原因，我国多地的空气质量状况不容乐观。持续恶化的空气质量状况已严重影响了中国的经济发展和公众的身体健康。随着我国空气质量监测体系的逐步完善，我国已建成多层次的空气质量监测网络。空气质量指数（Air Quality Index，AQI）根据大气环境中二氧化硫（SO2）、二氧化氮（NO2）、一氧化碳（CO）、臭氧（O3）、可吸入颗粒物（PM2.5、PM10）浓度值计算得出用于表示空气清洁或污染程度。提高空气质量分析和预测的科学性与准确性可以帮助政府提升对空气质量评价、管理和决策的可靠性，及时采取有效的防控措施规避大气污染造成的损害，保护公众健康。

早期的空气质量预测方法主要包括数值预测和回归统计［1］。数值预测方法通过利用多个环境监测站的监测信息建立气象排放和化学模型来模拟污染物的迁移、交换、扩散和排放过程［2］。该方法受复杂的先验知识、不可靠和有限的数据以及各种使用约束［3］，因此用来模拟真实的大气环境具有一定理论难度。回归统计方法避免了复杂的理论模型，通过使用基于统计的模型来预测空气质量。然而影响空气质量的各项因子与大气污染物浓度之间复杂的线性或非线性关系很难用确定的数学模型进行描述［4］。

随着物联网与传感器技术的快速发展和应用，城市中各种传感器及相关数据采集设备采集的大气数据为空气质量预测提供了必要的数据来源。由于传统的浅层学习模型在处理空气质量这类大数据方面仍存在瓶颈，因此新的空气质量预测方法需要数据驱动模型的支持［5］。文献［6］利用长短期记忆（Long Short-Term Memory，LSTM）网络来挖掘空气质量数据中存在的深层次时间依赖特征，通过提取输入序列中的长时间依赖关系对空气质量进行预测。由于LSTM 网络无法对空气质量间复杂的空间相关性进行建模分析，因此预测精度较低。文献［7］提出基于历史空气污染物浓度数据、气象数据和时间戳数据的空气污染物浓度预测LSTME（Long Short-Term Memory Extended）模型。该模型能够对具有长时间依赖性的时间序列进行建模，并能自动确定最优滞后时间。然而LSTME 模型随着预测步长的增加，其预测性能有所下降。文献［8］提出一个通用且有效的DAL（Deep Air Learning）模型来解决细粒度空气质量中的插值、预测和特征分析。该模型主要思想在于嵌入式特征选择以及对深度学习网络中不同层的半监督学习，利用未标记空气质量数据的相关信息来提高插值和预测性能。

除了对空气质量数据间的时间相关性进行建模外，非线性空间依赖性也是影响空气质量预测性能的重要因素之一。由于地面环境监测站呈现非均匀分布，因此如何将空间特征处理嵌入到各种基于神经网络的方法中一直是以往工作中的难题。一些折中的方法尝试将卷积神经网络（Convolutional Neural Network，CNN）应用于欧氏空间，通过人工将监测站点重新排列为二维阵列来挖掘其中的空间依赖性。如文献［9］采用融合CNN 和LSTM 结构的ConvLSTM（Convolutional Long Short-Term Memory）模型来模拟站点测量数据间的时空关系。但该模型是基于CNN 构建的网络，因此最适用于欧氏数据中的空间关系。为了使城市中多个环境监测站点间的空间特征处理能够嵌入到深度学习方法中以进一步提高空气质量预测精度，本文利用图卷积网络（Graph Convolutional Network，GCN）使原先只适用于处理欧氏数据的卷积操作扩展至可处理任意图数据的特点［10］，提出一种基于GCN、门控循环单元（Gated Recurrent Unit，GRU）网络、LSTM 网络构成的时空混合STAQI（Spatio Temporal Air Quality Index）模型用于空气质量预测。

本文主要贡献如下：

1）对门控循环单元网络进行改进。通过将图卷积网络嵌入门控循环单元，使该网络对输入数据具有空间特征提取的能力。这使原本适用于处理时间序列的门控循环单元网络可同时提取数据间时空依赖特征，同时与长短期记忆网络结合，提出一种新型的空气质量预测模型。

2）为防止过拟合问题的发生，通过在原有损失函数的基础上加入L2正则化项来降低模型复杂度和不稳定性。

3）在真实的数据集中从不同角度评估STAQI模型和其他多种模型的预测性能，验证了该模型具有最佳预测效果以及较强的泛化能力。

1 问题分析

空气质量监测站通过在站内安装多参数自动传感器来连续自动对周围空气质量进行监测。城市中部署的环境监测站分布于不同的地理位置空间并以一定时间间隔进行自动监测。因此监测站点产生大量具有空间坐标和时间戳的数据，这些数据被称为时空数据［11］。

从空间维度来看，某一区域的环境污染排放会受其他空间单元环境污染排放空间溢出效应的影响［12］。地理层次较高的位置具有较粗的粒度信息，父节点粒度由其子节点粒度组成。例如，一个监测站位于某一地区，该监测数据能准确反映周围区域细粒度空气质量状况。而此地区又位于某一城市，整个城市粗粒度空气质量信息由该城市各监测站点的监测数据共同决定。此外，两个站点间的地理距离与两地空气质量相关性成正比。

从时间维度来看，大气污染物排放影响因素的变化过程往往是缓慢的，当前污染排放积累值会受到前期污染排放的影响。对监测数据中每个实例的时间戳按时间顺序进行排序可生成顺序属性，其中相邻的时间戳通常比远处的时间戳具有更高的相似性。

综上所述，空气质量间的动态时空相关性可表示为两部分：第一是各站点传感器间相关性。从图1 中可以看出不同传感器时间序列之间的空间相关性是高度动态的，并随时间不断变化。第二是传感器内相关性。地理感知时间序列通常遵循周期性变化模式（如图1中站点4产生的时间序列），并随时间与地理位置的不同而变化［13］。因此，空气质量预测是一个典型的时空序列预测问题，时间与空间依赖关系应该被明确建模。

图1 多站点间的动态时空相关性Fig.1 Dynamic spatio-temporal correlation between multiple sites

2 时空混合STAQI模型

2.1 STAQI模型结构

STAQI 模型由全局组件和局部组件构成，对目标区域污染物以及周围邻近区域内空气质量动态转化对目标站点空气质量预测产生的影响进行分析研究。在不用人为处理数据提取特征的情况下，STAQI 模型通过反复训练可从大量有监督数据集中自动学习空气质量数据中动态时空依赖特征进而对目标站点进行细粒度空气质量预测。该模型结构如图2 所示，下面对STAQI模型实现过程进行主要介绍。

图2 STAQI模型结构Fig.2 Structure of STAQI model

2.1.1 全局组件

城市各监测站点间的空气质量并不是相互孤立而是存在一定相关性。通过选取北京市东四、天坛与官园站点同一时段内空气质量数据进行对比，结果如图3 所示，可以发现各站点空气质量随时间具有相似的变化趋势。因此全局组件从时空依赖的角度分别进行建模并融合以提取邻近站点空气质量对预测产生的影响。

图3 东四、天坛、官园站点空气质量对比Fig.3 Comparison of air quality at Dongsi，Tiantan and Guanyuan sites

1）空间依赖性建模。

城市中分布的各监测站点间距并不是等同的，因此构成的拓扑网络为图结构，这意味着无法使用CNN 处理这类非欧氏数据以提取空间特征。GCN是一种对图数据进行深度学习的方法［14］，其核心思想是学习一个函数映射使得图中的节点可以聚合自身节点和邻居节点的特征来生成节点新表示。

定义1拓扑图G。利用未加权图G=(V，E)来描述城市各环境监测站间的地理位置拓扑结构。每个站点作为图中的一个节点，V 代表城市中所有站点的集合，即V={V1，V2，…，VN}，N 为监测站点总个数。E 代表各监测站点间边的集合。由于大气环境是一个实时动态变化的系统，根据地理第一定律，各站点间存在不同程度的影响关系。因此利用式（1）来计算两两站点间的距离并取其倒数作为连边权重值存储在邻接矩阵A中，A ∈RN×N。

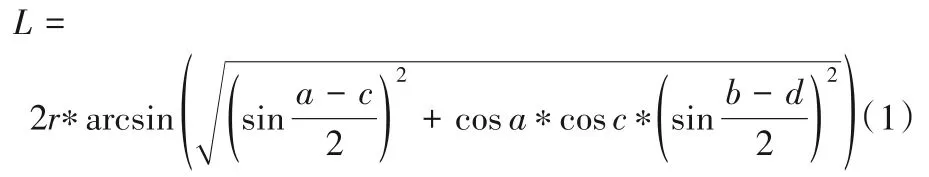
其中：X(a，b)、Y(c，d)代表两个站点位置，a、c为纬度，b、d为经度，r为地球半径。

定义2特征矩阵XN×P。将目标站点所在城市各环境监测站历史AQI 值作为网中节点的属性特征，表示为X ∈RN×P。P 代表节点属性的数量特征，即历史时间序列长度。Xt∈RN×i表示i时刻城市所有环境监测站的AQI 当前值。

GCN通过利用目标站点所在城市各环境监测站地理位置拓扑结构G 和特征矩阵X 的信息学习复杂映射函数以提取空间特征，主要步骤如下：

①根据目标站点所在城市各环境监测站地理位置构建拓扑图G和邻接矩阵A。

②利用各站点监测数据的AQI信息构建特征矩阵X。

④利用式（2）提取特征矩阵中的空间信息：其中：σ(⋅)表示激活函数表示第i 层权值矩阵表示第i层的激活值，且

2）时间依赖性建模。

循环神经网络（Recurrent Neural Network，RNN）是一个可用于处理时间序列的网络［15］。然而，在实际的运用中会存在梯度消失、梯度爆炸等问题［16］，因此传统的RNN 在时序预测方面存在一定的局限性。GRU 是RNN 的一种变体结构，该网络具有结构相对简单、参数较少、训练能力较快等优势。因此在全局组件中利用GRU 网络提取邻近站点空气质量数据间的时间依赖特征。

全局组件原理如图4 所示。首先根据目标站点所在城市各环境监测站地理位置信息构成拓扑图，根据拓扑图计算生成相应的邻接矩阵、度矩阵和拉普拉斯矩阵。利用GCN 根据拉普拉斯矩阵来动态捕获各环境监测站的不同影响权重，获得空间特征。其次将提取空间特征后的时间序列作为GRU的输入，通过单元之间的信息传递获取时间特征。由于GRU整体输出为最后一个单元时刻的隐藏状态，它的维度不同于标签向量，因此最后通过全连接层做维度转换。图5 左侧显示了全局组件预测过程，其中每一个循环单元结构简称为GG（GCN GRU），右侧显示了GG 单元细胞具体结构，ht-1表示t -1时刻的输出，GCN 是图卷积操作，输入数据xt经过GCN 生成xt'，ut、rt分别是t 时刻的更新门和重置门，ct为t 时刻细胞状态，ht表示t时刻的输出。

全局组件计算过程如下所示：其中：f(A，Xt)表示图卷积过程，W和b代表训练过程中的权重和偏置。

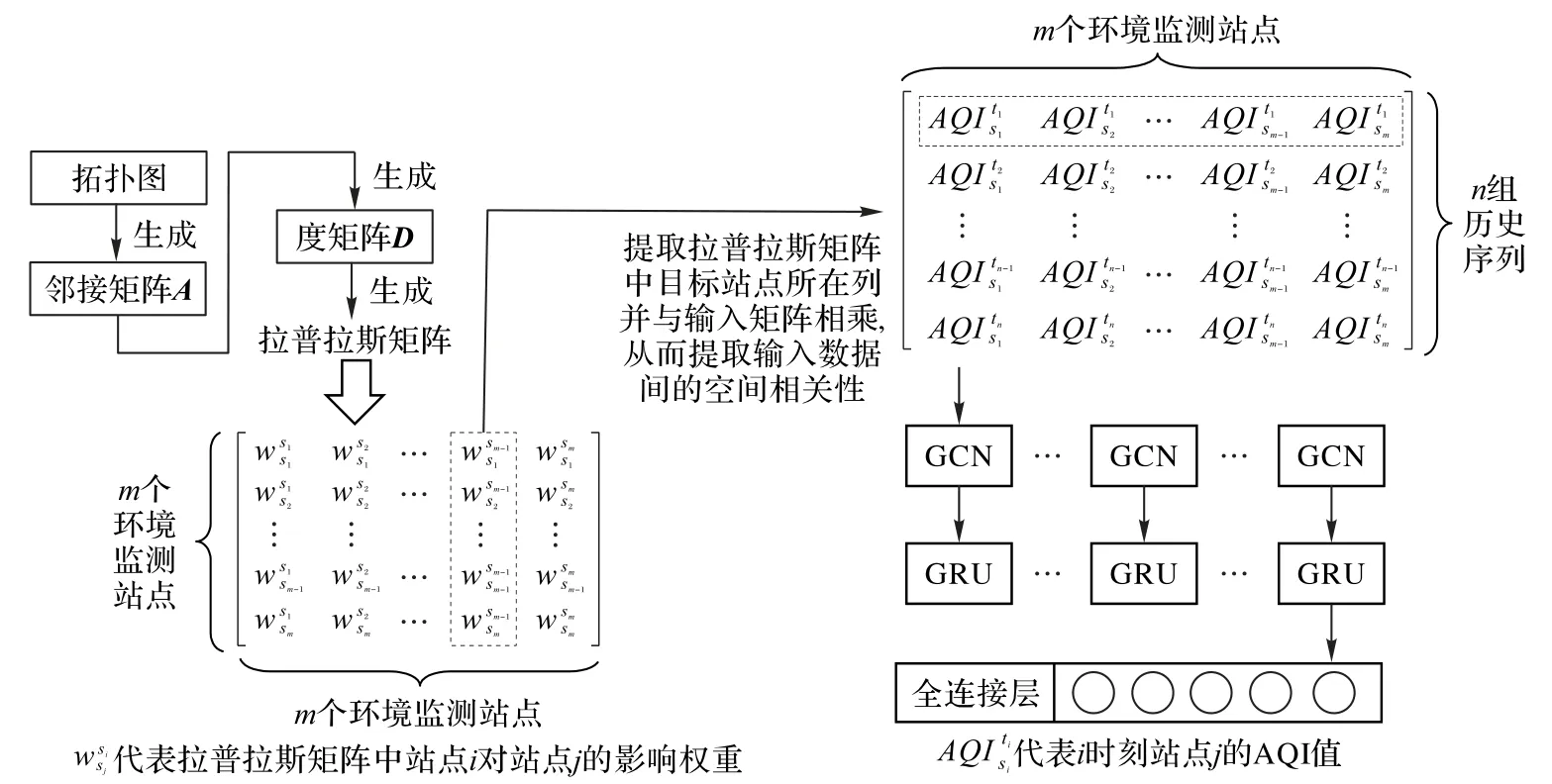
图4 全局组件原理Fig.4 Principle of global component

图5 全局组件预测过程Fig.5 Prediction process of global component

2.1.2 局部组件

一方面，当前空气质量状况会受到过去一段时间内污染物累积的影响；另一方面，站点监测到的空气质量数据是一组具有一定周期性的序列。比如一个工厂周期性地排放污染气体，那么附近站点的空气质量可能会随着时间的推移而重复。因此空气质量在时间维度上既具有短期性质，也具有长期性质。

LSTM 在传统RNN 基础上通过在隐藏层各神经单元中增加记忆单元从而使时间序列上的记忆信息可控［17］。LSTM 单元细胞由遗忘门ft、输入门it和输出门ot构成［18］，各部分更新公式如下所示：

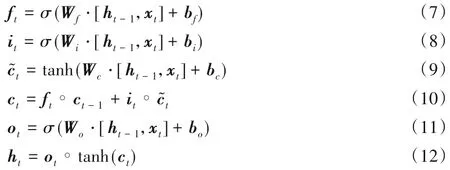
其中：∘表示按元素乘，W 和b代表训练过程中的权重和偏置，ht、ct分别表示t时刻的隐藏状态和细胞状态。

局部组件以目标站点过去n 个时间步长的本地污染物浓度与目标站点AQI值作为输入，通过LSTM网络提取输入数据中的时间相关特性，最后将LSTM 的输出经过全连接层转换成与标签向量一致的维度，从而得到局部组件的输出。局部组件的训练算法主要包含以下3个步骤：

1）前向计算LSTM 每个神经元的输出值，即分别根据式（7）～式（12）计算ft、it、ct、ot、ht向量值。每个时刻的隐藏状态ht接入输出层，经过Softmax 函数后取得预测值，进而得到残差E：

2）反向计算每个神经元的误差项δ 值。误差项的反向传播包括两个方面：一个是沿时间轴的反向传播，即根据t 时刻的误差项δt来计算t -1 时刻的误差项δt-1。其中δt定义为则t -1时刻的误差项δt-1为：

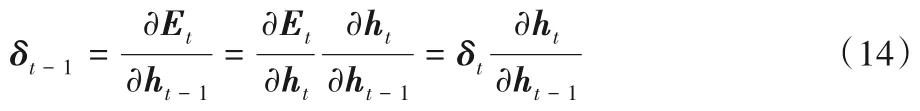
另一个是将误差向上一层传播。即假设当前为第l 层来计算l -1层的误差项。

3）根据相应的误差项来计算各权重矩阵和偏置向量的梯度（共计12个），从而更新各参数。

2.1.3 组件融合

STAQI 模型采用加权融合的方式来联合局部组件输出ov与全局组件输出oc以形成目标站点AQI预测值Y，其计算过程如下所示：

其中α 为组合权值（0 ≤α ≤1）。在实验部分，将对组件分配不同权重从而进行预测性能对比并根据实验结果选取α最佳取值。

2.2 损失函数

模型训练过程以最小化损失函数为目标，使模型更精确地拟合训练数据。但若模型参数w 太多，会导致模型复杂度大大提高，模型在训练集上具有出色的拟合效果，但在测试集上性能欠佳。因此本文在原有的损失函数L0(w)基础上加入L2 正则化项来对权重系数加以约束限制，使得模型尽量简单，整体的损失函数L(w)可表示为：

对L(w)进行求导：

对参数w更新如下所示：

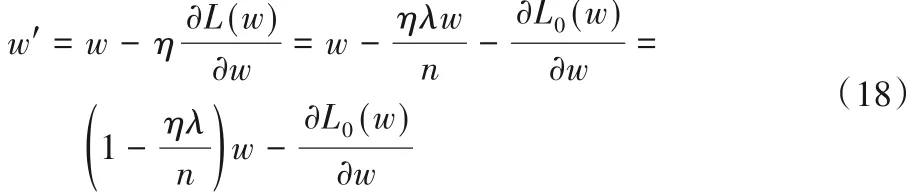
由此可以看出当w 趋于0 时，加入L2 正则化项可以使得参数减小到很小范围内，从而降低模型复杂度。综上所述，STAQI 模型中使用的损失函数如式（19）所示，其中用Yt和来表示目标站点实际AQI值和预测AQI值。损失函数中第一项用于最小化站点实际AQI值与预测AQI值之间的误差。第二项Lreg是L2正则化项，有助于避免过拟合问题，λ为超参数。

2.3 STAQI模型算法流程

输入 测试数据；

输出 预测值。

1）初始化模型多组超参数值。

2）加载邻接矩阵A和数据集。

3）使用Min-Max方法将数据归一化到[-1，1]。

4）根据不同时间窗口，利用滑动窗口机制构建有监督数据集和测试集。

5）根据批尺寸大小计算训练总批次。

6）搭建全局组件。首先实现GG 单元细胞结构，通过继承RNNCell类改写_init_和_call_方法来实现。_init_方法中需要指定激活函数、节点数量、隐藏单元数量并获取根据邻接矩阵计算得到的拉普拉斯矩阵。_call_方法中对输入数据进行变化，通过提取拉普拉斯矩阵中目标站点所在列与原始输入数据相乘，利用提取空间特征后的输入数据新表示来计算GRU 单元细胞状态。调用自定义GG 细胞类，利用最后单元状态输出值通过全连接层转化成与标签向量相同的维度。

7）搭建局部组件。设置LSTM 节点数量和隐藏单元数量，利用LSTM 网络最后单元输出值作为全连接层的输入，作维度转化。

8）融合全局组件与局部组件输出。

9）定义损失函数和均方根误差。

10）使用Adam优化器以最小化损失值为目标。

11）定义以训练总批次为循环次数的循环体，在循环体中首先实现对训练集中输入数据的划分，即划分为全局组件与局部组件输入。其次调用已定义的全局和局部组件。最后将当前批次局部组件输入、全局组件输入、标签数据作为填充数据来动态执行优化器、损失函数值以及预测值的计算。

12）对训练好的模型输入测试数据进行测试，获得模型输出值。

13）将模型输出值进行反归一化处理，得到模型实际预测值并输出。

3 实验与结果

3.1 数据获取与处理

本文选取北京地区35个环境监测站从2014年4月1日至2019 年12 月31 日的历史监测信息作为实验数据集。数据从http：//beijingair.sinaapp.com 网站中获得。空气质量监测数据为小时粒度信息，包括SO2、NO2、CO、O3、PM2.5、PM10六种大气污染物浓度值和AQI 值。通过在Pycharm 开发环境中安装配置Tensorflow框架并使用Python编程语言来完成有关实验。

收集的数据必须经过预处理才可作为STAQI 模型的输入，主要由于以下两方面原因：第一，外界多种不确定性因素的干扰导致收集的数据中存在某些时间序列或属性值缺失，因此需要遍历整个数据集对缺失的时间序列进行插入并利用空值填充方法填充其他特征数据项。第二，空气质量受多重因素影响，各影响因子量纲不同。为保证模型预测性能，本文采用Min-Max 方法将数据归一化到[-1，1]，最终在评价模型的预测效果时，再将预测值重新还原到原来的大小并与真实值进行比较。整个数据集按照8∶2比例划分为训练集和测试集用于模型训练及测试。训练集中的每条数据由同一时刻目标站点6 种污染物浓度值和目标站点所在城市各环境监测站点AQI值组成。

3.2 实验

3.2.1 实验流程

本实验首先需要收集相关实验数据，对收集的数据进行预处理使数据变得完整以符合模型的输入要求。其次将整个数据集划分为训练集与测试集。利用训练集中的数据，使用滑动窗口机制来建立模型输入和输出结果之间的关系从而构成有监督数据集。每条有监督数据集由特征窗口和标签窗口构成。通过将大量有监督数据集作为模型输入并在一定迭代次数内不断训练调整模型参数，使得模型可以学习特征和标签之间复杂的非线性关系。最后使用测试集对训练好的模型性能进行测试，在面对只有特征没有标签的数据时，训练好的STAQI模型可以推断出与之对应的标签进而完成空气质量预测任务。STAQI模型的整个实验流程如图6所示。

图6 STAQI模型实验流程Fig.6 Experimental flowchart of STAQI model

3.2.2 评价指标

为了评估STAQI 模型训练后的预测性能，本文使用均方根误差（Root Mean Square Error，RMSE）来评估站点空气质量真实值与预测值之间的差异，RMSE 数值越低表示模型的预测精度越高，其计算公式如下所示：

3.2.3 模型超参数设置

模型超参数的不同取值对模型预测性能将产生一定影响，主要包括迭代次数、网络深度、学习率、输入层的向量大小、隐藏层单元数量、批尺寸等超参数［19］。本实验采用Adam优化器，手动设置学习率为0.001，批尺寸为64，迭代次数为300。为了最小化隐藏单元数量的不同取值对STAQI 模型预测性能产生的客观影响，将从［8，16，32，64，100，128］中选择不同的隐藏单元数量进行实验，结果如表1所示。在固定α取值为0.5时，当增加隐藏单元数量时，RMSE值先降低后增加。这主要是因为当隐藏单元数量大于一定阈值时，模型复杂度和计算难度大大增加，从而增加了预测误差。当隐藏单元数量为64 时，RMSE 误差值最小，因此在实验中将LSTM 模型与GRU模型中的隐藏单元数量设置为64。

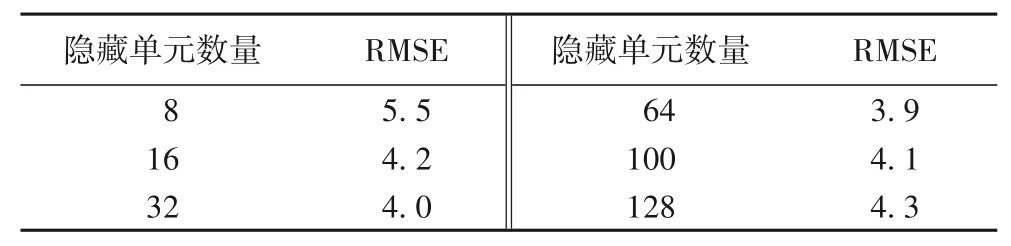
表1 隐藏单元数量对RMSE的影响Tab.1 Influence of number of hidden cells on RMSE

此外，由于STAQI 模型输出是一个局部组件和全局组件的加权参数值α（0 ≤α ≤1）。为设置α 的最佳取值，本文在0.0 和1.0 之间改变α 大小来比较模型RMSE 值，实验结果如表2 所示，选取RMSE 最低值对应的0.6 作为本实验中α 的取值。通过对α参数寻优的结果可以发现局部组件具有更大的权重，这意味着本地污染物浓度对目标站点空气质量预测产生的影响要高于邻近站点空气质量对目标站点空气质量预测产生的影响。

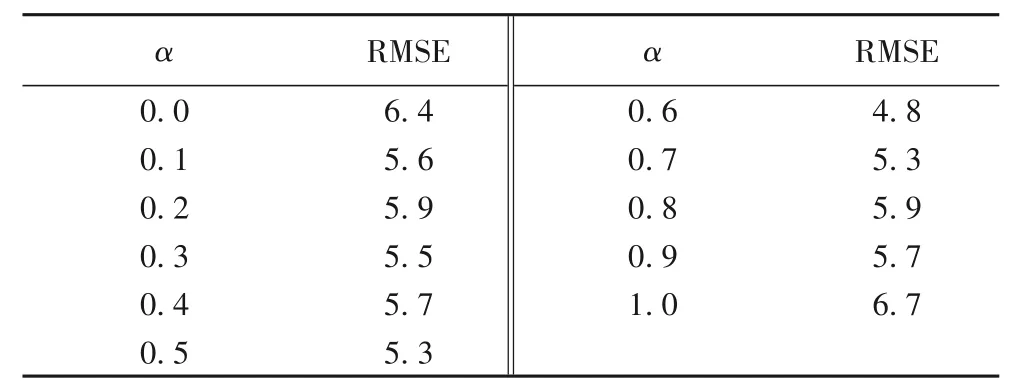
表2 α取值对RMSE的影响Tab.2 Effect of α value on RMSE

3.3 结果与分析

3.3.1 基准模型比较

本节从不同时间窗口和预测不同目标站点两个方面将STAQI 模型与自回归综合移动平均模型（Auto Regressive Integrated Moving Average model，ARIMA）、支持向量回归（Support Vector Regression，SVR）［20］、反 向 传 播（Back Propagation，BP）神经网络［21］、GRU 进行对比。其中SVR 使用线性核函数，惩罚项为0.001。

1）基于不同时间窗口的空气质量预测。

利用时间窗口描述模型使用过去N小时的历史数据来预测未来T小时后的目标站点空气质量，简记为(N，T)。通过使用不同基准模型对北京市东四监测站点进行预测，实验结果如表3 所示。从表3 可以得到以下四方面结论：第一，GRU 模型强调了时间特征建模的重要性，通常比其他基线模型（如ARIMA、SVR、BP 模型）具有更高的预测精度。第二，基于时空特性的STAQI 模型与只考虑时间特征的GRU 模型相比能获得更好的预测效果。第三，对于包含时序处理模块的模型（如GRU、STAQI 模型）来说，在相同预测步长的情况下，模型输入的历史数据越多，可进一步提高其预测能力。第四，无论时间窗口如何变化，STAQI 模型都可以通过训练获得最佳预测性能，相较于基线模型中性能较优的GRU 模型，STAQI 模型RMSE 值大约下降19%。因此STAQI 模型不仅可以用于短期预测，还适用于中长期预测。

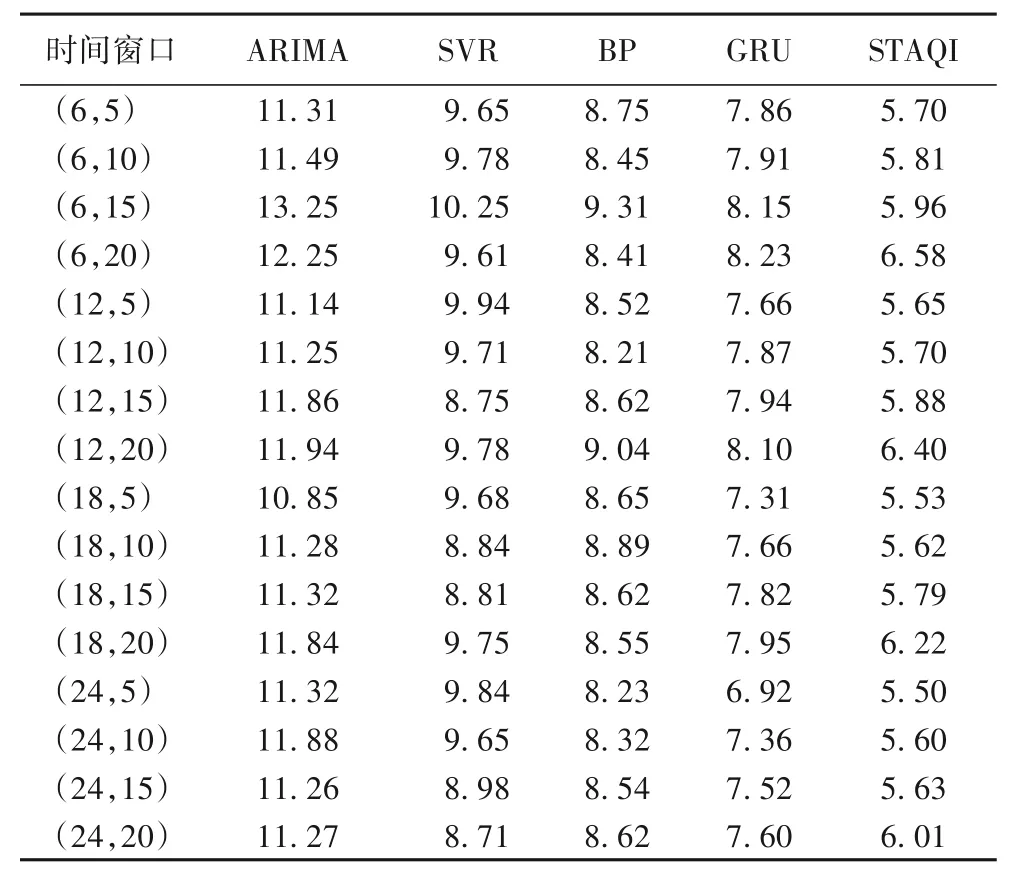
表3 不同时间窗口的预测结果Tab.3 Prediction results of different time windows

2）基于不同目标站点的空气质量预测。

为检验STAQI模型对不同目标站点的预测能力是否具有显著差异，本文使用不同基线模型对北京市天坛站点未来一定时间步长的AQI进行预测，实验结果如表4所示。从表4可以发现STAQI模型相比其他基线模型对于任意AQI预测步长仍能取得最佳预测性能。其中与性能较优的GRU 模型相比，STAQI 模型RMSE 值大约下降6%，因此STAQI 模型对地理位置不同、具有地势差异的不同站点的空气质量预测能力具有较强的泛化性。

表4 不同模型对天坛站点AQI预测的RMSE值Tab.4 RMSE values predicted by different models for AQI of Tiantan site

此外，对于北京市35 个环境监测站点，本文使用不同基准模型对各环境站点未来一定时间步长的空气质量进行预测并统计各模型最优预测站点数量，实验结果如表5 所示。从表5 可以看出在对未来1 h 的短期预测中各模型的最优预测站点数量大致相同，但随着预测窗口逐渐增大，ARIMA、SVR、BP 模型对空气质量这类时空数据预测能力越来越低。由于GRU 模型是一种专门用于处理时间序列的网络，随着预测步长增加，其最优站点统计数量要高于ARIMA、SVR 和BP 模型，但低于STAQI 模型。基于时空混合的STAQI 模型随预测步长的增加相比其他基线模型显示出明显的预测优势。

表5 不同模型最优预测站点数统计Tab.5 Statistics on the number of optimal prediction sites by different model

3.3.2 变体模型比较

为了检验STAQI模型中各个组件对模型预测性能的有效性，本文将STAQI模型与由GCN 和GRU 构成的全局组件模型（LOCAL）和由LSTM 构成的局部组件模型（GLOBAL）进行比较，实验结果如表6所示。从表6可以看出对于不同预测步长STAQI 模型的RMSE 都取得最低值。相较于变体模型中性能较优的局部组件模型，STAQI 模型RMSE 值大约下降16%。这是由于局部组件模型只考虑了空气质量数据中的时间特性，忽略了空间相关性。而全局组件模型把对目标站点的空气质量预测完全依赖于邻居节点的空气质量状况，忽略了本地污染物浓度对目标站点空气质量预测的影响。STAQI模型将时间与空间、局部与全局因素进行结合，使得该模型可以更好地拟合空气质量变化趋势，提高预测精度。

表6 变体模型预测的RMSE值比较Tab.6 Comparison of RMSE values predicted by variant models

此外本文对北京市35 个环境监测站点未来6 h 的空气质量使用变体模型和STAQI 模型分别进行预测，各模型的RMSE 值如图7 所示。从图7 可以发现对于任一站点STAQI模型的RMSE 都取得最低值，因此融合了全局组件和局部组件的STAQI模型可以提高对空气质量的预测能力。

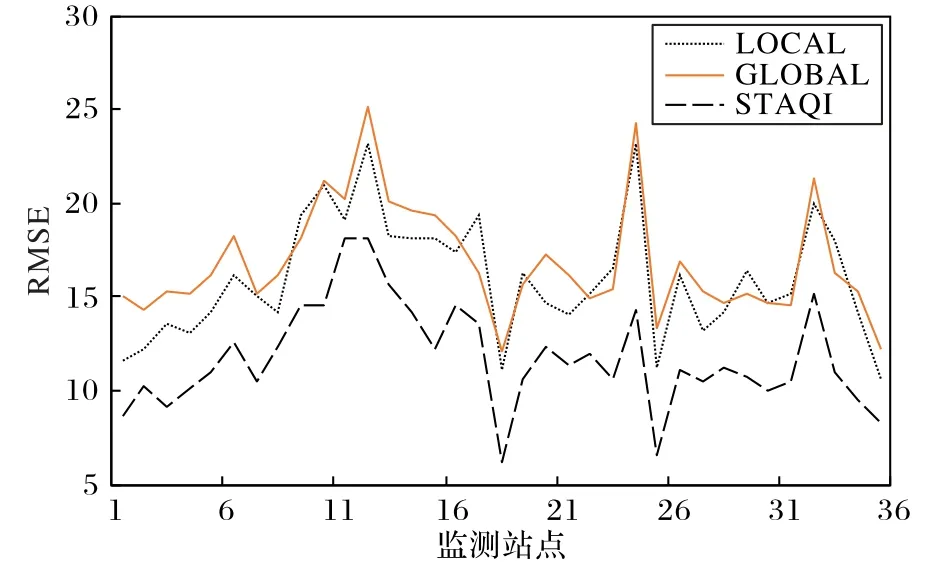
图7 变体模型对北京市35个站点的预测结果比较Fig.7 Comparison of prediction results of variant models for 35 sites in Beijing

3.3.3 模型预测及改进分析

为了直观显示STAQI 模型在真实数据集中的预测效果，本文使用STAQI 模型对东四站点进行预测，实验结果如图8所示。从图8 可以看出STAQI 模型通过提取空气质量中存在的时空特征可以很好地拟合空气质量变化趋势；但是STAQI模型在拐点处的预测误差要大于对平稳序列预测的误差，这是由于受极端天气条件如暴风、暴雨等影响，导致空气质量在极短的时间内发生突变。因此在未来工作中，可以在模型中融合气象因素以提高模型在空气质量拐点处的预测能力。

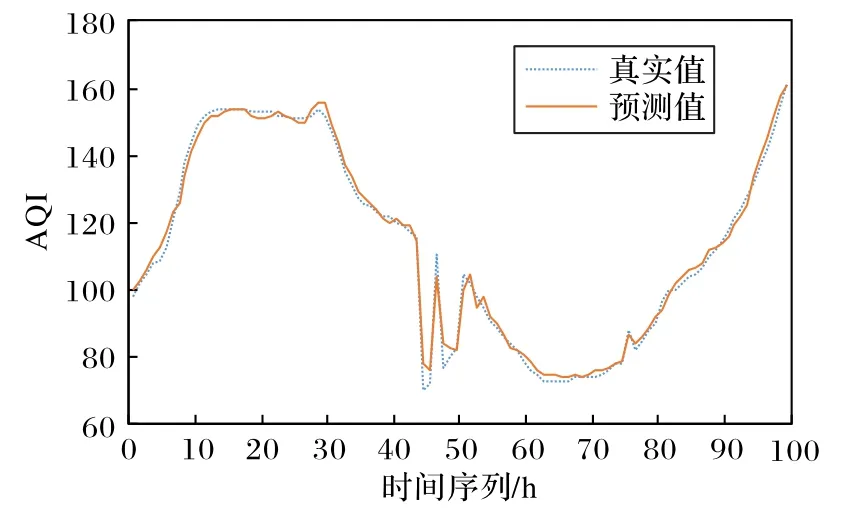
图8 STAQI模型对东四站点的预测结果Fig.8 Predicted results of STAQI model for Dongsi site

4 结语

针对空气质量间存在的复杂时空特征，本文提出一种面向空气质量的新型STAQI 时空混合预测模型，它由全局组件和局部组件构成。该模型对地面多个环境监测站之间的时空依赖性进行明确建模，可以自动学习多变量空气质量相关时间序列数据局部趋势的相关特征和时空依赖模式。与传统仅考虑时间相关性的方法相比，STAQI 模型在保留原有监测站点位置分布的基础上将空间特征处理嵌入深度学习方法中以同时提取城市中多站点间的复杂时空相关性。通过在真实的数据集上进行评估，并与不同基准模型和变体模型在不同预测水平下进行比较，结果表明STAQI 模型对空气质量预测具有更精准的预测效果。

为了进一步提高模型预测性能，未来研究工作中将以以下两方面作为研究重点。首先，空气质量受多种复杂因素影响，仅仅利用污染数据和空气质量数据作为影响因素具有一定片面性，因此可以在模型中融合气象因素、交通流量等其他影响因子对问题进行建模。其次，可在LSTM 网络中引入注意力机制，使得该网络对不同时期的历史数据可分配不同权重的注意力，从而获得更精准的预测。