基于最大信息系数的ReliefF和支持向量机交互的自动特征选择算法

葛倩，张光斌，张小凤

（陕西师范大学 物理学与信息技术学院，西安 710119）

0 引言

在不同领域的数据挖掘过程中，产生了包含众多特征的高维数据集，其中，冗余特征和不相关特征的存在不但会增加数据处理过程的复杂度，还在一定程度上降低了后续分类算法的准确率［1］。因此，对高维数据集进行预处理，减少冗余特征和不相关特征成为数据挖掘的重要研究内容。

作为数据降维的一种有效方式，特征选择算法不仅可以筛选出数据的重要特征，规避维数灾难造成的分类准确率低的问题，还可以降低计算的复杂度，提高分类模型的性能［2］。特征选择算法主要分为过滤式（Filter）、包装式（Wrapper）与嵌入式（Embedded）方法三类［3-6］。其中，包装式特征选择算法在特征选择的过程中是以分类器的分类性能评价特征子集，如K近邻算法、序列特征选择（Sequential Feature Selection，SFS）等［7］。但包装式特征选择算法每次选择特征时均要执行分类算法以判断特征子集的优劣，因此算法的计算效率较低［8］。嵌入式特征选择方法，是将特征选择过程和学习模型的训练过程在同一个优化过程中完成，并使用同一个目标函数来实现特征筛选，如正规化方法、决策树算法等［9］。嵌入式特征选择方法可以快速地选择特征子集，但是目标函数的构造是一大难点［10］。过滤式特征选择方法使用准则函数来评估特征相较于目标类的相关性或鉴别能力，因其克服了包装式与嵌入式特征选择方法计算复杂性高的缺点被广泛用于数据的预处理［11-12］。常见的过滤式特征选择方法主要有互信息（Mutual Information，MI）、相关系数、最大相关最小冗余（max-Relevance and Min-Redundancy，mRMR）算法、Relief 算法等［13］。其中，由Kira等［14］在1992 年提出的Relief 算法是一种高效的过滤式特征选择算法，因其复杂性低、高效快速而适用于处理高维数据，该算法在二分类问题中显示出较好的性能［15］。1994年，Kononenko［16］提出了扩展的Relief 算法，即ReliefF 算法，该算法不仅可以解决多分类问题，还可以解决数据缺失和存在噪声的问题，已被广泛应用于多个领域［17-18］；但是ReliefF 算法在应用中存在稳定性不足、特征权值波动较大的问题。为此，Wang等［19］提出在给定样本时，根据局部样本的平均偏差计算其权重的方法来提高特征选择方法的稳定性。同时，改进已选取的近邻样本之间相关性的计算方法也可以用来提高ReliefF 算法的稳定性［20-22］。但是，目前所提出的大多数改进算法均忽略了近邻样本的选取方式对于算法稳定性的影响；此外，这些改进的ReliefF 算法由于缺乏与分类模型的交互，对于特征的选择标准没有明确的评价指标，从而在利用筛选出的特征子集进行后续的分类问题时可能会出现分类准确率较低的问题［23］。为了解决这一问题，赵玲等［24］提出利用支持向量机（Support Vector Machine，SVM）与特征选择算法实现信息交互以自动寻找特征子集的方法；但是，由于每次实验训练集的随机性，筛选的特征子集仍具有较大的随机性，不具有泛化能力。

为了实现最优特征子集的自动筛选，缓解维数灾难造成的分类准确率降低问题，本文提出一种可以筛选出稳定的特征子集且具有泛化能力的特征选择算法。首先，对传统ReliefF 算法的近邻样本选取方法进行改进，提出MICReliefF（Maximum Information Coefficient-ReliefF）算法，利用最大信息系数（Maximal Information Coefficient，MIC）［25］替代欧氏距离估计样本之间差异，寻找同类与异类近邻样本；其次，将选择的特征子集输入到SVM 分类器，以SVM 的分类准确率作为评价指标，多次寻优，自动确定其最优特征子集，实现MICReliefF 算法与分类模型的交互优化，即MICReliefF-SVM自动特征选择算法。利用UCI 多个公开数据集对MICReliefF-SVM 算法的性能进行了验证，并且利用SVM 模型与极限学习 机（Extreme Learning Machine，ELM）对MICReliefF-SVM 自动特征选择算法筛选的特征子集进行测试。

1 ReliefF算法

ReliefF 算法是一种具有低计算复杂度的过滤式特征选择算法。首先，从总样本D中随机选取样本R；然后，在数据中找出与样本R属同一类的k个最近邻的样本，记作Hj，与样本R不在同一类中的k个最近邻的样本，记作M(C)j；最后，计算样本中特征A的特征权重，公式如下：

其中：class(R)是随机选取的样本R所属的类别；P(C)是类别C出现的概率；P(class(R)是随机选取的样本R所属类别的概率；diff(A，R，Hj)和diff(A，R，M(C)j)分别表示两样本在特征A下的距离；m是抽样次数。在ReliefF 算法中，近邻样本数通常设置为k=10［26］。

ReliefF 算法的伪代码如下所示。

算法1 ReliefF 算法。

输入 数据集D=，特征个数a，迭代次数m，近邻样本的个数k。

输出 特征权重向量W。

ReliefF 算法的目标是通过多次评估随机选取的样本实例与同类近邻样本和异类近邻样本之间的类间距离和类内距离，计算每个特征的权重，挑选出权值高的特征，从而完成特征选择的任务［27］。但是，ReliefF 算法在寻找近邻样本时，采用的是相似度度量，如果随机抽取的样本较少，将导致特征权值波动较大，进而影响特征排名。近邻样本的选取对于算法的稳定性具有较大的影响。在选择近邻样本时，ReliefF算法通过使用欧氏距离来计算所有样本与所随机选取的样本实例R的相似程度，以便从同类与不同类样本中分别选择k个距离最小，即相关性最大的样本作为近邻样本。尽管欧氏距离已经成为评定两个样本之间相近程度的一种常见度量方式，但它普适于样本的各个特征度量的标准比较统一的情形。对绝大部分真实数据集来说，样本中每个特征的取值不是统一的标准，因而会导致近邻样本的选取极易被特征值较大的特征所影响，从而忽略了特征值较小的特征对于分类准确率的贡献。

2 MICReliefF-SVM 自动特征选择算法

为了提高ReliefF 算法的性能，本文使用最大信息系数（MIC）来代替欧氏距离求解样本之间的相关性，即MICReliefF 算法。

MIC 是一种用来捕捉属性间相关性的统计量［25］，能够有效度量变量之间的复杂关系。

对于数据集D={U=ui，V=vi}，i=1，2，…，N，变量和变量的互信息可以表示为：

其中：p(u，v)是变量U、V的联合概率密度；p(u)、p(v)分别是变量U、V的边缘概率密度。

变量U和变量V的MIC 定义为：

其中：a、b是在x、y轴方向上划分的格子个数，应满足|a| ·|b| ＜B，B=N0.6，N是样本数。

尽管ReliefF 算法能够计算特征所占的权重，但由于缺乏与分类模型的交互，且对于特征子集的选择标准没有明确的评价指标，因此，ReliefF 算法本身无法去除冗余特征。在实际应用中，一般都是根据已有经验设置权重阈值，大于阈值的特征被保留下来，而小于阈值的特征则被剔除，这样就会导致不当的阈值选择对分类结果产生不好影响。如果将MICReliefF 算法排序后的特征输入到SVM 分类器，利用SVM模型的分类准确率来选择特征子集，通过多次交互寻优，则可以自动确定其最优特征子集，即MICReliefF-SVM 自动特征选择算法。算法的流程如图1 所示。

3 实验与结果分析

为了验证MICReliefF-SVM 自动特征选择算法的性能，使用UCI 公开数据库中乳腺癌数据集WDBC、电离层数据集Ionosphere、马腹绞痛数据集Horse Colic、蘑菇数据集Mushroom、帕金森数据集Parkinsons、声纳、地雷、岩石数据集Connectionist Bench 以及检测是否有新分子的Musk 数据集共7 个常用于分类问题研究的数据集［28］对算法的特征选择能力进行了测试。表1 为所选数据集的信息，以及每一次实验时随机选取的训练集和测试集的个数。

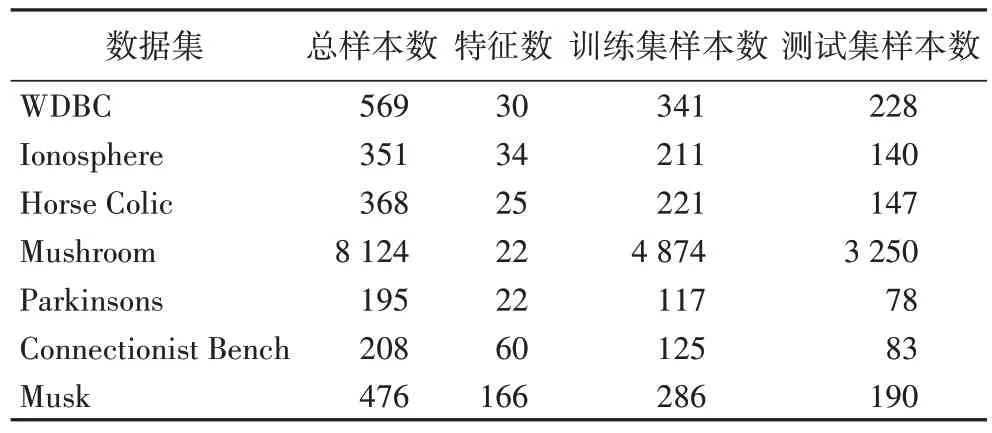
表1 实验数据集的信息Tab.1 Information of experimental datasets

实验中分别采用ReliefF-SVM 算法和MICReliefF-SVM 算法对7 个数据集中的特征进行筛选，每次实验采用随机抽取的方式将每个数据集的总样本划分成60%的训练集与40%的测试集，利用训练集对SVM 模型进行训练，选出分类准确率最高的特征子集，并将其应用到测试集进行测试。为了能选择出稳定的最优特征子集，重复实验过程500次，统计500次实验中测试集出现的最优特征子集及其出现的次数，最后把500 次实验中出现次数最多的最优特征子集作为最终的最优特征子集，筛选结果如表2 所示。从表2 中给出的筛选后的特征个数结果可知，与ReliefF-SVM 算法相比，在7 个UCI 数据集上MICReliefF-SVM 算法除对Connectionist Bench数据集筛选后保留相同的特征个数之外，在其他数据集上都筛除了更多的冗余特征，即能有效地减少样本的特征维度。

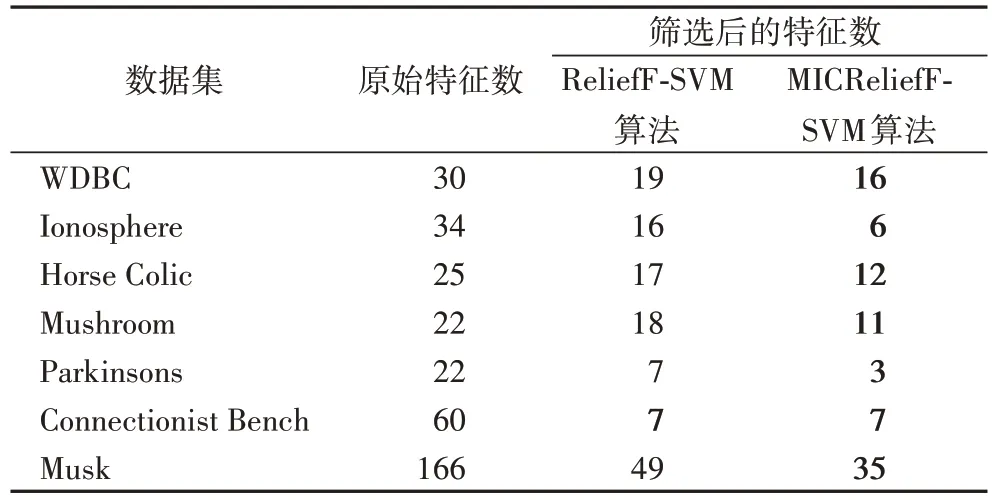
表2 各算法的特征筛选结果比较Tab.2 Comparison of feature filtering results of different algorithms

为了验证MICReliefF-SVM 算法所选特征子集的分类效果以及稳定性，利用SVM 与ELM 两种分类模型，分别对表2筛选出的特征进行测试，即分别采用SVM 与ELM 两种分类模型对利用MICReliefF-SVM 算法选取的特征子集、ReliefFSVM 算法选取的特征子集以及原始数据集中的全部特征进行分类。在SVM 分类器中，采用RBF（Radial Basis Function）核函数，核参数C=1，γ=100［11］；在ELM 分类器中，采用Sigmoid 核函数，隐层节点的个数设置为20［29］。每次实验仍按照表1 所示的标准划分训练数据集与测试数据集，实验100次，以平均准确率Acc（Accuracy）、平均敏感度Sen（Sensitivity）、平均特异性Spe（Specificity）、平均精准度Pre（Precision）以及平均F 值（F-measure）等作为评价指标。上述评价指标基于表3 混淆矩阵计算，其定义如下：

表3 混淆矩阵Tab.3 Confusion matrix

SVM 分类模型中各评价指标的平均值及其标准差如表4 所示。从表4 的数据可知：

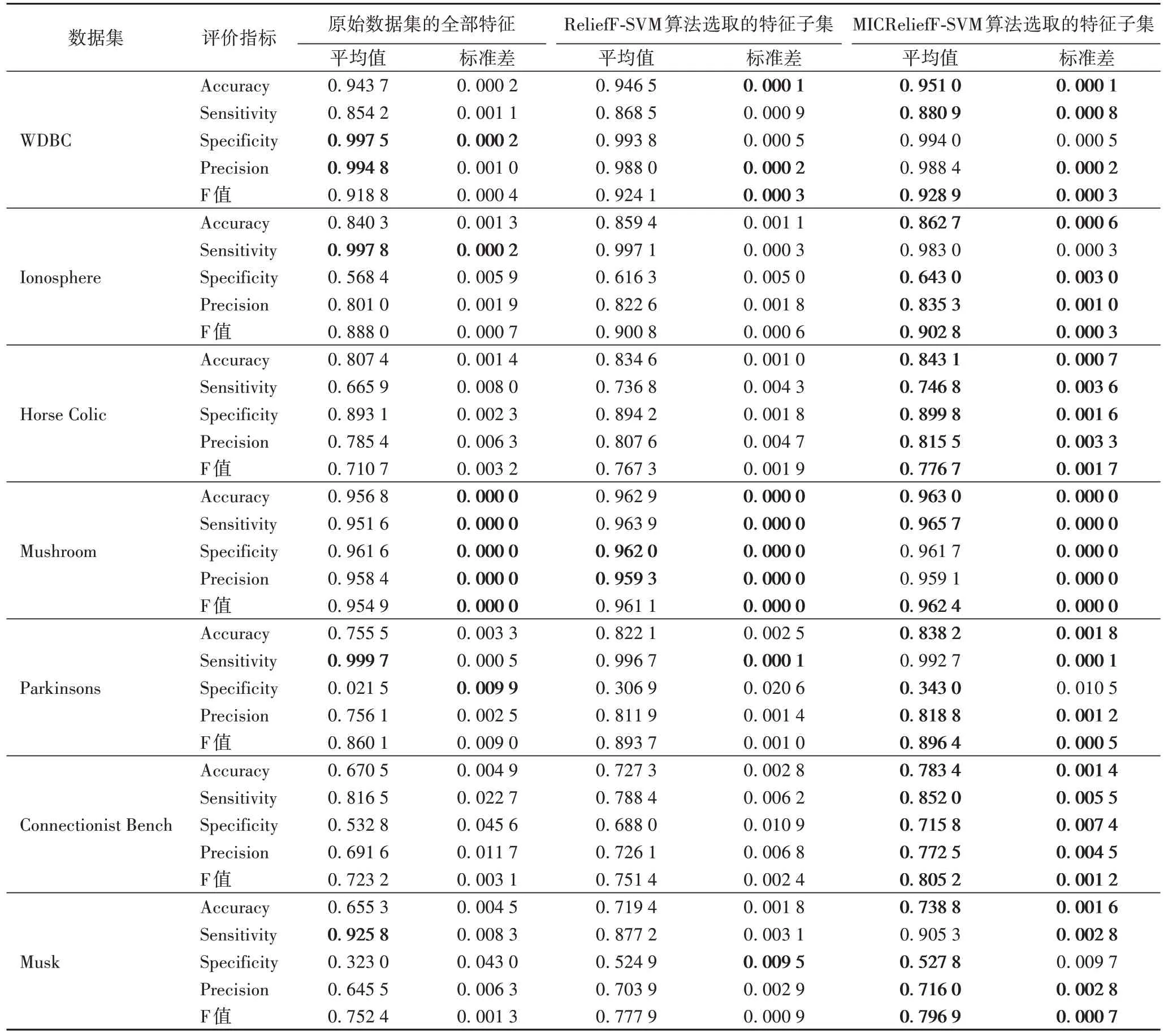
表4 各特征选择算法在SVM模型中评价指标的平均值与标准差比较Tab.4 Mean and standard deviation comparison of evaluation indexes among each feature selection algorithms in SVM model

1）在WDBC 数据集中，利用ReliefF-SVM 算法与MICReliefF-SVM 算法选取的特征子集的Accuracy、Sensitivity、F 值指标的平均值均优于采用原始数据集中的全部特征，且MICReliefF-SVM 算法结果整体最优。对于标准差而言，除Specificity外，Accuracy、Sensitivity、Precision、F 值的标准差均优于采用原始数据集中的全部特征。

2）在Ionosphere 数据集中，除Sensitivity 指标外，利用ReliefF-SVM 算法与MICReliefF-SVM 算法选取的特征子集的Accuracy、Specificity、Precision、F 值的平均值及其标准差均优于采用原始数据集中的全部特征，且MICReliefF-SVM 算法结果最优。

3）在Horse Colic数据集中，利用ReliefF-SVM 算法与MICReliefF-SVM 算法选取的特征子集的各指标的平均值及其标准差均优于采用原始数据集中的全部特征，且MICReliefF-SVM 算法结果最优。

4）在Mushroom 数据集中，利用ReliefF-SVM 算法与MICReliefF-SVM 算法选取的特征子集的Accuracy、Sensitivity、Specificity、Precision、F 值的平均值均优于采用原始数据集中的全部特征，其中，MICReliefF-SVM 算法选取的特征子集的Accuracy、Sensitivity、F 值指标结果优于ReliefFSVM 算法。对于标准差而言，利用ReliefF-SVM 算法与MICReliefF-SVM 算法选取的特征子集与原始数据集在精确到小数后4 位时，标准差均为0。

5）在Parkinsons 数据集中，除Sensitivity 指标外，利用ReliefF-SVM 算法与MICReliefF-SVM 算法选取的特征子集的各指标的平均值均优于采用原始数据集中的全部特征，且MICReliefF-SVM 算法结果最优，利用ReliefF-SVM 算法与MICReliefF-SVM 算法选取的特征子集的各指标的标准差均优于采用原始数据集中的全部特征。

6）在Connectionist Bench 数据集中，利用MICReliefFSVM 算法选取的特征子集的各指标的平均值及其标准差均优于利用ReliefF-SVM 算法选取的特征子集以及采用原始数据集中的全部特征，除Sensitivity 指标的均值外，利用ReliefF-SVM 算法选取的特征子集各指标的平均值及其标准差均优于采用原始数据集中的全部特征。

7）在Musk 数据集中，利用ReliefF-SVM 算法与MICReliefF-SVM 算法选取的特征子集的Accuracy、Specificity、Precision、F 值指标的平均值均优于采用原始数据集中的全部特征，且MICReliefF-SVM 算法结果整体最优。对于标准差而言，MICReliefF-SVM 算法选取的特征子集的指标除Specificity 劣于ReliefF-SVM 算法外，Accuracy、Sensitivity、Precision、F 值的标准差均优于ReliefF-SVM 算法选取的特征子集和采用原始数据集中的全部特征。

ELM 分类模型中各评价指标的平均值及其标准差如表5 所示。

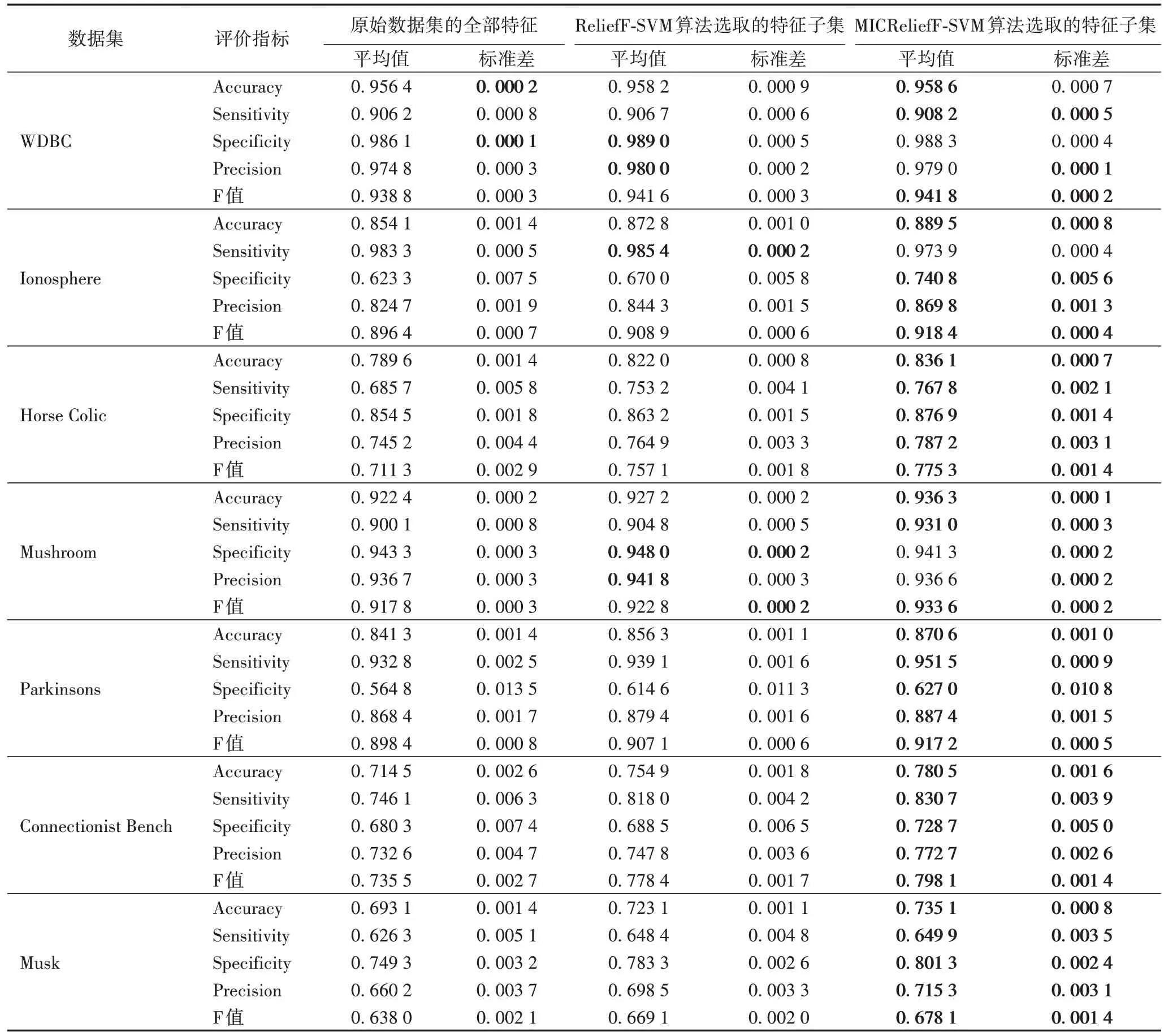
表5 各特征选择算法在ELM模型中评价指标的平均值与标准差比较Tab.5 Mean and standard deviation comparison of evaluation indexes among each feature selection algorithms in ELM model

从表5 可知：

1）在WDBC 数据集中，利用ReliefF-SVM 算法与MICReliefF-SVM 算法选取的特征子集的各指标的平均值均优于采用原始数据集中的全部特征；其中，利用MICReliefFSVM 算法选取的特征子集的Accuracy、Sensitivity 以及F 值指标的平均值高于ReliefF-SVM 算法选取的特征子集。对于标准差而言，利用ReliefF-SVM 算法与MICReliefF-SVM 算法选取的特征子集的Sensitivity、Precision、F 值指标的标准差均优于采用原始数据集中的全部特征。

2）在Ionosphere 数据集中，除Sensitivity 指标外，利用MICReliefF-SVM 算法选取的特征子集的Accuracy、Specificity、Precision、F 值的平均值及其标准差均优于利用ReliefF-SVM 算法选取的特征子集以及采用原始数据集中的全部特征，且ReliefF-SVM 算法选取的特征子集各指标的平均值及其标准差均优于采用原始数据集中的全部特征。

3）在Horse Colic 数据集中，利用ReliefF-SVM算法与MICReliefF-SVM 算法选取的特征子集的各指标的平均值及其标准差均优于采用原始数据集中的全部特征，且MICReliefF-SVM 算法结果最优。

4）在Mushroom 数据集中，利用MICReliefF-SVM 算法选取的特征子集的Accuracy、Sensitivity、F 值的平均值均优于利用ReliefF-SVM 算法选取的特征子集与采用原始数据集中的全部特征，且ReliefF-SVM 算法选取的特征子集各指标的平均值均优于采用原始数据集中的全部特征；对于标准差而言，利用ReliefF-SVM 算法与MICReliefF-SVM 算法选取的特征子集的标准差整体优于采用原始数据集中的全部特征。

5）在Parkinsons、Connectionist Bench 和Musk 数据集中，利用ReliefF-SVM 算法与MICReliefF-SVM 算法选取的特征子集的各指标的平均值及其标准差均优于采用原始数据集中的全部特征，且MICReliefF-SVM 算法结果最优。

SVM 模型与ELM 模型的测试结果均证明，MICReliefFSVM 算法可以在减少样本特征维度的同时，有效提高分类准确率，该算法不仅能够自动选择出分类准确率良好的特征子集，而且选取的特征子集具有一定的稳定性和泛化能力。

为了探究MICReliefF-SVM 算法的计算效率，本文统计了采用SVM 与ELM 两种分类模型对MICReliefF-SVM 算法选取的特征子集、ReliefF-SVM 算法选取的特征子集以及原始数据集中的全部特征进行分类时100 次实验的总运行时间，结果如表6 所示。

从表6 可以看出：在SVM 和ELM 两种分类模型中，对MICReliefF-SVM 算法选取的特征子集、ReliefF-SVM 算法选取的特征子集进行分类的运算时间均短于对原始数据集中的全部特征进行分类的时间，其中MICReliefF-SVM 算法选取的特征子集的分类时间最短，即计算效率最高。说明本文提出的MICReliefF-SVM 算法可以有效地提高后续学习算法的计算效率，进一步说明了MICReliefF-SVM 算法的有效性。

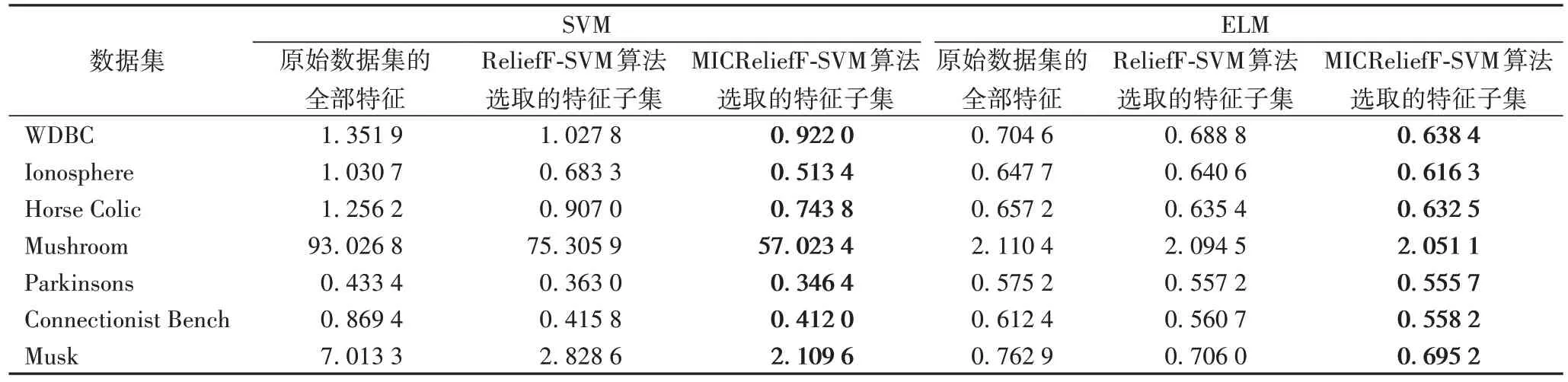
表6 不同特征选择算法在SVM模型和ELM模型中的运行时间比较 单位：sTab.6 Comparison of running time among different feature selection algorithms in SVM model and ELM model unit：s

为进一步验证MICReliefF-SVM 算法的有效性，本文在7个数据集上分别利用SVM 与ELM 分类模型比较了MICReliefF-SVM 算法与MI、mRMR、支持向量机递归特征消除（Support Vector Machines-Recursive Feature Elimination，SVM-RFE）、相关性特征选择（Correlation-based Feature Selection，CFS）、随机森林（Random Forest，RF）、遗传算法（Genetic Algorithm，GA）［30-33］六种经典的传统特征选择算法的分类准确率，每次实验仍按照表1 所示的标准划分训练数据集与测试数据集，实验100次，求其平均准确率作为评价标准。

各特征选择算法在SVM 分类模型中的实验结果如表7所示。从表7 中给出的结果可知：MICReliefF-SVM 算法除了在Mushroom 数据集上的准确率稍劣于RF 特征选择算法外，在其他6 个数据集上的准确率均优于对比算法。各特征选择算法在ELM 分类模型中的实验结果如表8 所示。从表8中给出的结果可知：MICReliefF-SVM 算法除在Mushroom 数据集和Musk 数据集上的准确率劣于RF 特征选择算法，在其他6 个数据集上的准确率均优于对比算法。因此，MICReliefF-SVM 算法所选特征子集的分类能力整体上要优于对比算法。

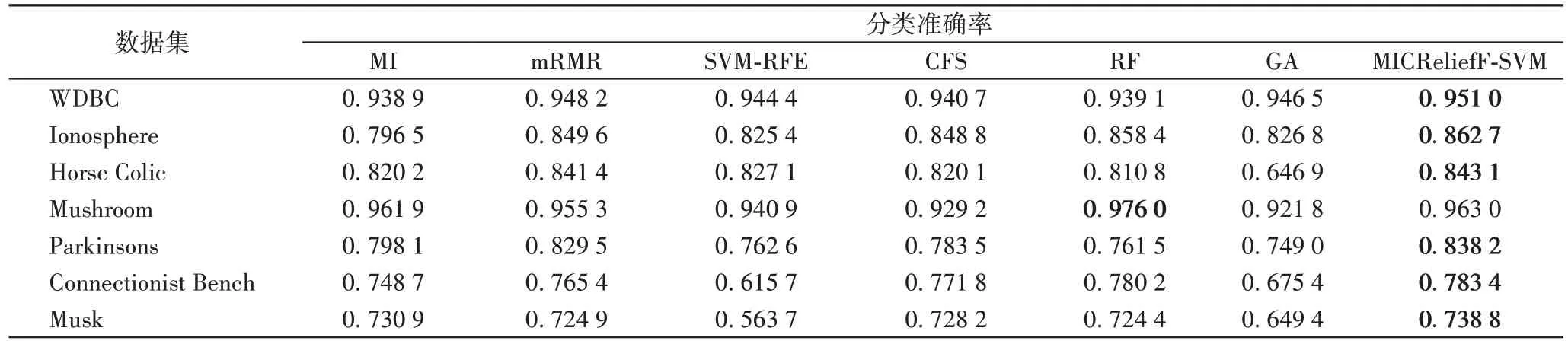
表7 不同特征选择算法在SVM模型中的分类准确率对比Tab.7 Comparison of classification accuracy among different feature selection algorithms in SVM model

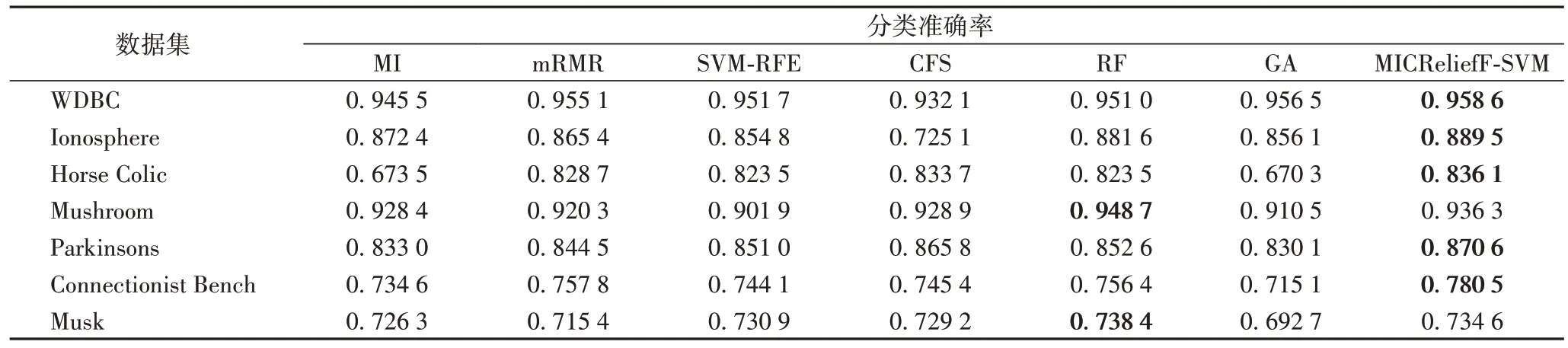
表8 不同特征选择算法在ELM模型中的分类准确率对比Tab.8 Comparison of classification accuracy among different feature selection algorithms in ELM model

4 结语

本文提出了一种MICReliefF-SVM 交互的自动特征选择算法，采用多个UCI 数据集对算法的有效性进行验证。研究结果表明：

1）与ReliefF 算法相比，MICReliefF-SVM 算法在特征冗余的筛选上具有一定的优势。利用SVM 与ELM 分类模型对UCI 多个公开数据集上的数据进行分类的对比实验结果表明，MICReliefF-SVM 算法在减少样本特征维度的同时，有效提高了分类准确率，且该算法可以实现分类准确率良好的特征子集的自动选择，选取的特征子集具有一定的稳定性和泛化能力。

2）与经典MI、mRMR、SVM-RFE、CFS、RF 以及GA 特征选择算法相比，MICReliefF-SVM 算法所选特征子集整体上具有更好的分类能力。

在未来的工作中，将会继续对提高ReliefF 算法的稳定性以及该算法在处理高维特征数据方面的应用进行研究。