北斗/GNSS 机载动态PPP 性能分析

赵龙，郭将，栗广才，罗锋

(1.武汉大学 测绘学院,武汉 430079；2.自然资源部航空地球物理与遥感地质重点实验室,北京 100083；3.武汉大学 卫星导航定位技术研究中心,武汉 430079)

0 引言

自上世纪美国的GPS 建成以来，在相当长一段时间内卫星导航定位领域主要以GPS 定位为主，但随着21 世纪以来俄罗斯的GLONASS 现代化计划的实施，使得GLONASS 焕发新生；中国的北斗卫星导航系统(BDS)历经“三步走”战略也已经实现全球组网，面向全球用户提供服务；欧盟的Galileo 系统也在持续建设和发展.当前全球卫星导航系统(GNSS)已由原来的单GPS 主导逐渐发展为多系统鼎足而立的阶段，多系统融合定位已经成为当前卫星导航定位技术领域的主要发展趋势之一[1-3].GNSS 多系统融合定位相比单系统定位而言，具有可见卫星数更多、卫星几何构型更好以及可以利用多频观测值组合成波长更长的新观测量，使得模糊度参数能更快被固定[4].

精密单点定位(PPP)是指利用高精度的载波相位观测值以及卫星星历来实现高精度单点定位的技术，它只需要架设一台接收机，就能实现厘米级甚至毫米级定位精度，自其出现以来就有十分显著的应用优势[5].相比相对定位技术，它不受距离限制，作业方便；此外，由于避免差分运算对观测信息造成的损失，PPP 技术也能应用于气象监测等方面.由于上述特点，近年来PPP 技术已经成为GNSS 领域的热门研究方向，展现出了广阔的应用前景.如今以国际GNSS 服务(IGS) 组织推动的多模GNSS 实验跟踪网(MGEX)为契机，PPP 进一步朝着多系统融合的方向发展[6].

近年来，许多学者对多系统PPP 技术进行了大量研究，文献[7]进行了多系统PPP 实验，结果表明多系统在定位稳定性和精度上均优于单系统；文献[8]研究分析了四系统融合PPP 的定位性能，实验表明，在单系统几何观测、几何构型不理想的区域，多系统融合能显著提高PPP 的定位精度和收敛速度；文献[9]对比分析了 GPS、BDS、GPS+BDS 不同情况下静态与动态PPP 精度，结果表明多系统状态下定位精度更高.文献[10]对多系统的PPP 性能进行了分析，结果发现BDS+GPS 的定位精度优于其他组合.

目前PPP 技术的研究主要采用MGEX 的测网数据进行多系统组合静态或者静态模拟动态实验，对于实际的动态场景尤其是航空动态数据解算中的多系统PPP 的定位性能研究较少[11].因此，本文选用机载动态场景下的实测的数据，利用IGS 提供的精密产品，实现了对单GPS、单BDS 和BDS+GPS 组合定位系统，BDS+GPS+GLONASS 组合系统动态模型下的消电离层组合(IF)的PPP 解算，通过对可视卫星数、位置精度衰减因子(PDOP)、验后残差以及平面和高程方向定位精度等方面对定位性能进行了评估和分析.

1 数学模型

1.1 原始观测方程

PPP 广泛使用伪距和载波相位观测值进行解算.相对论效应、电离层延迟、对流层延迟、天线相位中心偏差(PCO)、相位中心变化(PCV)、潮汐效应均对最终的定位精度产生影响[12]，考虑到上述误差改正后的观测方程为：

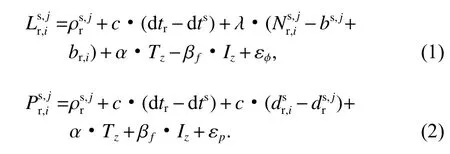
式中：P、L分别为伪距和载波相位观测值，单位为m；上标j、s 分别为卫星系统和卫星，下标r、i分别为接收机和测站；ρ 为卫星与接收机之间的几何距离，单位为m；c为真空中的光速；dtr、dts分别为接收机端钟差和卫星钟差，单位为m；λ 为载波的波长；为整周模糊度；bs,j、br,i分别表示卫星端和接收机端相位硬件延迟；ds,j、dr,i分别表示卫星端和接收机端的伪距硬件延迟偏差，单位为m；α 为对流层投影系数；Tz为天 顶对流层 延迟；βf为电离层对应投影系数；Iz为天顶电离层延迟；εφ、εp分别为载波相位与伪距观测噪声，单位为m.

1.2 无电离层组合观测方程

对于多频的伪距和载波相位观测值而言，为了消除电离层延迟的影响，可以通过构造无电离层组合，此时观测方程为[13]：

式中：f1和f2分别为两个载波的频率；P1、P2分别为两个频率上的伪距观测值；L1、L2分别为两个频率上的相位观测值.式(1)～(2)的观测方变为：

在实际数据解算中，文献[14-15]指出接收机钟差、卫星钟差会分别吸收接收机伪距硬件延迟、卫星伪距硬件延迟；文献[16-17]说明了相位硬件延迟与整周模糊度参数的相关性较强，PPP 解算过程中卫星端和接收机端的相位延迟会被模糊度参数吸收，使得模糊度参数失去整数特性，式(5)～(6)就变为：

1.3 参数估计方法

本文进行PPP 参数解算时采用的是最小二乘估计，误差方程为

式中：Dii为方差矩阵，反映了精度信息；σ0为验前单位权中误差；Qii为协因数矩阵；1 为观测数；r为多余观测量.

2 数据来源与处理策略

2.1 数据来源

本实验为在海南省进行的动态机载实验，飞行时间自2021 年3 月27 日6 点29 分起，结束于当日11 点50 分(UTC 时间)，飞行轨迹如图1 所示.最终获得到的实测数据主要包括基准站数据和机载数据.

图1 飞机飞行轨迹图

基准站数据由基准站1 与基准站2 数据组成.基准站1 的坐标已知，基准站2 坐标未知，通过与基准站1 联测的方式可以获得基准站2 的坐标.基准站1 的数据为2 Hz 的单GPS 数据，其搭载的接收机类型为Spectra Precision PROFLEX800，数据起止时间为2021 年3 月27 日6 点14 分至12 点24 分(UTC 时间)，基准站2 数据情况与基准站1 相同.

机载数据由移动站搭载NovAtel Guiscard 接收观测得到，数据为2 Hz 的 GPS/BDS/GLONASS 的高频实测数据.

其中各系统包含频率分别为GPS 的L1/L2；GLONASS 的L1/L2 以及北斗二号(BDS-2)的B1I/B2I.采集时段从2021 年3 月27 日 6 点29 分起至11 点50 分(UTC 时间).

2.2 PPP 数据处理策略

采用表1 中的数据处理策略，解算时位置当作随机游走参数来估计，每历元以标准单点定位解作为初值；接收机参数视作噪声，大小给定为的白噪声参数进行估计，其中s 表示时间单位s；由于飞机速度很大，其所处对流层环境变化剧烈，因此本研究采用了每历元单独估计对流层参数的策略，随机游走噪声给定为

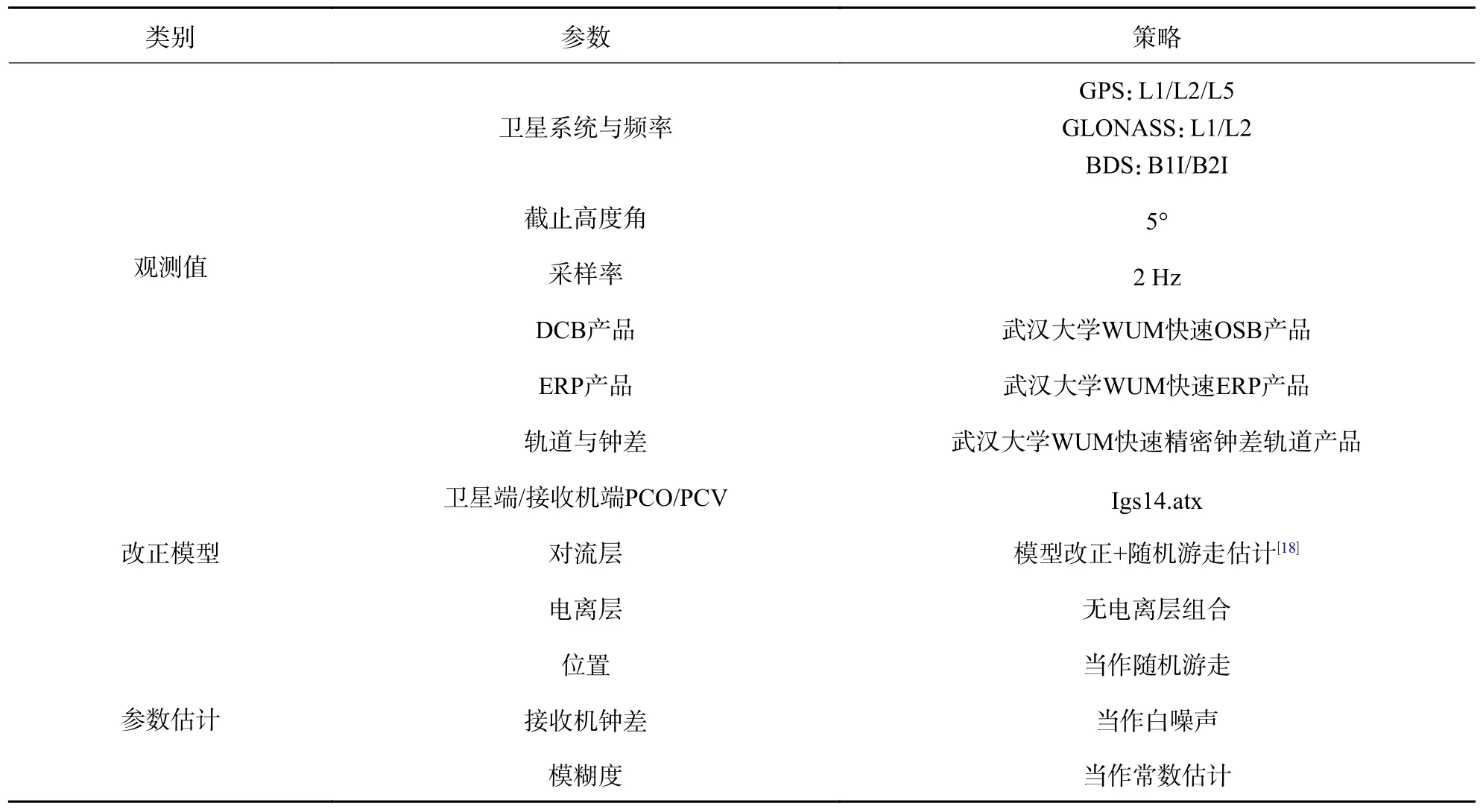
表1 数据处理策略

在数据处理时，为了获得参考真值，首先使用RTKLIB 软件对参考站和流动站做了双差解算，固定率为99.3%，这证明以此基线结果作为真值是可行可靠的.由于此次机载测量实验中北斗三号(BDS-3)缺少双频数据，无法构建双频的无电离层组合，因而本文中所使用的BDS 数据均是BDS-2 的数据.

使用PRIDE PPP-AR 软件处理动态数据，PRIDE PPP-AR 是由武汉大学PRIDE 课题组开发的一款可对多系统 GNSS 数据进行后处理，能应用于大地测量学、重力测量、摄影测量、地震监测等方面研究的开源软件.软件主要经过数据准备和预处理、最小二乘估计以及位置信息输出等步骤，输入精密星历文件和观测值文件最终解算出高精度单点定位坐标，软件处理具体流程如图2 所示

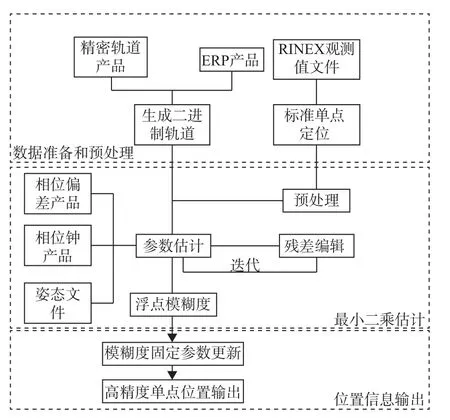
图2 PRIDE PPP-AR 数据处理流程图

3 实验结果与分析

3.1 可视卫星分析和PDOP 分析

由图3 可以看出，GPS 的卫星分布较均匀，在各个方向均有分布，几何构型也是其中最好的，BDS 的卫星多数分布在西南侧，东北侧的卫星分布较少，空间几何构型较差，GLONASS 的卫星分布较为均匀，但卫星数较少，因此分布较为稀疏，BDS+GPS+GLONASS 的卫星分布更加均匀，高程(U)方向分布的卫星数也更多.

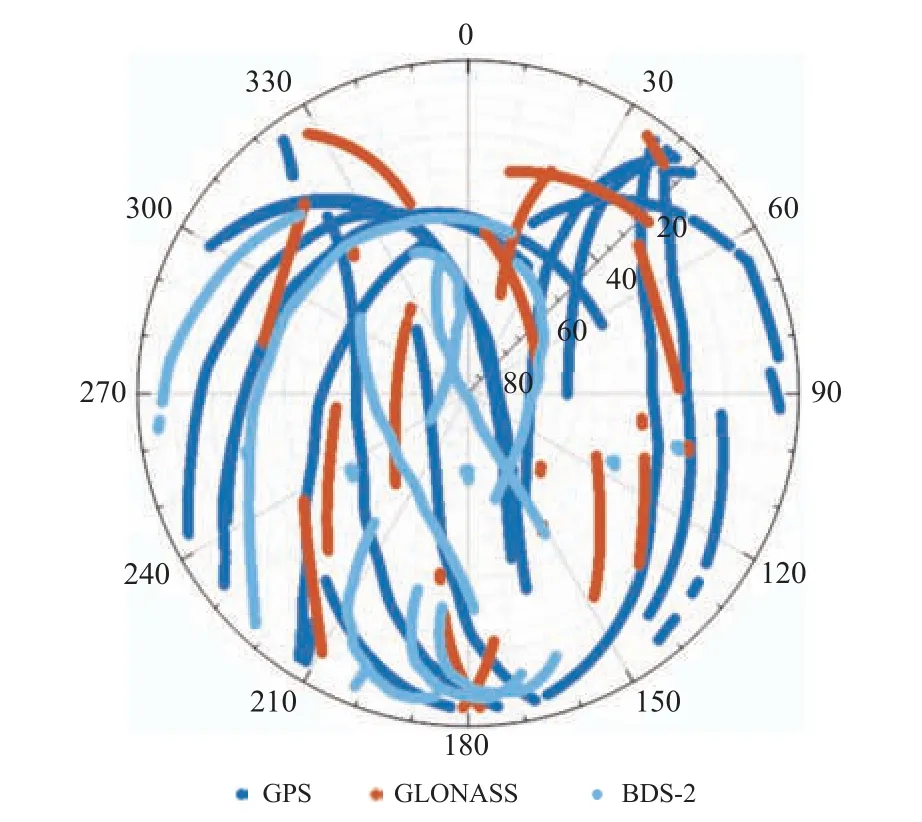
图3 GPS、BDS 和GLONASS 的卫星分布图

由图4 可知，GPS+BDS-2+GLONASS 的可视卫星数约为20～30 颗，飞行过程中约稳定在25 颗，相比单GPS、单BDS-2 在亚太地区拥有更多得可用卫星，平均10～15 颗，GLONASS 在观测的开始和结束阶段可视卫星7～9 颗，但观测过程大部分时间段内可视卫星数基本为零.多系统的卫星数显著多于单系统的卫星数，更加适合在动态情况部分卫星被环境遮挡时保持PPP 解算的准确估计和稳定持续解算.

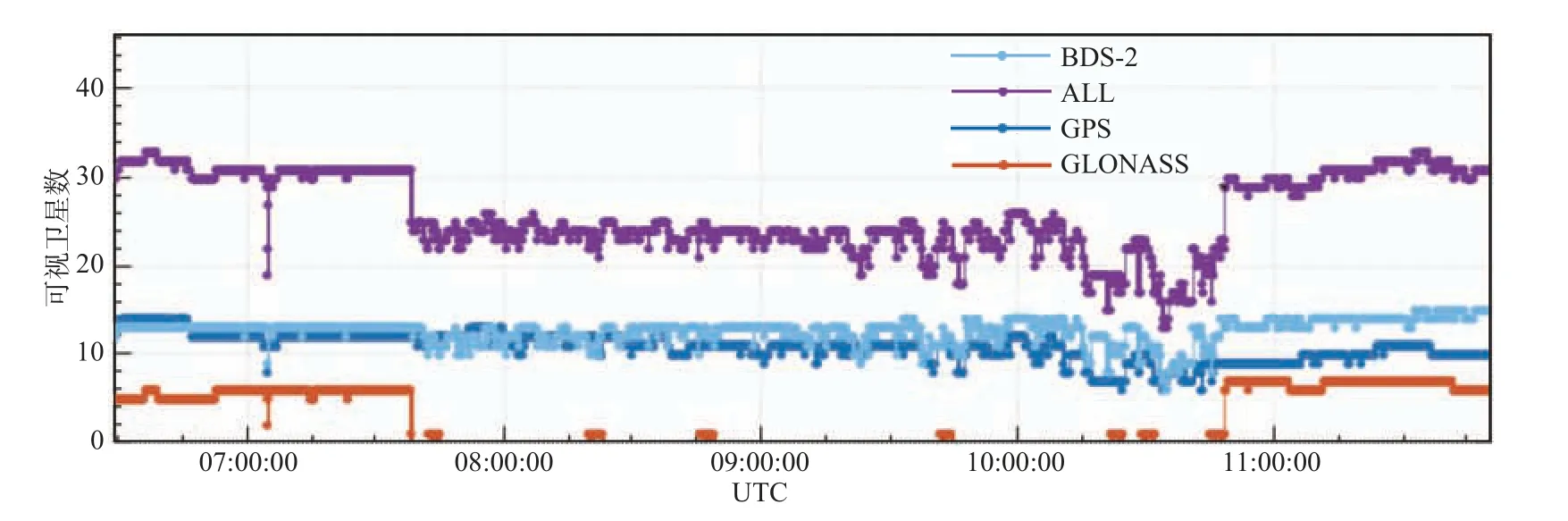
图4 可视卫星数的时间序列

PDOP 值反映了定位的质量情况，其值越小，表明其卫星处于较好的几何分布状态，定位精度更好.由图5 可知，单BDS-2 的PDOP 最大，其值在2 附近波动，单GPS 其PDOP 值在1.5 波动.GPS+BDS+GLONASS 的PDOP 值与GPS+BDS 相差不大，在1 附近波动，主要是因为GLONASS 在飞机起飞后其卫星数量急剧减少，推测是由于接收机未能有效跟踪GLONASS 卫星，因而实际的定位主要由BDS-2和GPS 决定.相比单系统而言，飞机飞行过程中的大部分时刻多系统的PDOP 降低了0.5～1 倍，有望获得更高的定位精度.

图5 三系统的PDOP 值和可用卫星数时间序列

结合表2 的定位精度情况，对于卫星数和几何构型更好的多系统PPP，其PDOP 更小，卫星分布更均匀，可见卫星数更多、定位精度更高，表明更多的卫星数以及更好的空间几何构型有助于提高机载动态情况下PPP 解算的精度.

3.2 观测值残差分析

观测值残差是由观测值减去改正值后以及参数估计值后的残余部分，包括机载测量过程中来自卫星端、信号传播路径中、接收机端等带来的噪声以及其他未被精确模型化的误差，观测值残差大小可以作为评价一个模型好坏以及观测质量的重要标准.

定位的精度与观测条件、数据质量直接相关、越精确的观测数据，其定位解算的结果就会相应越好.残差的噪声量级以及包含的周期信号可以用来分析观测值的数据质量.虽然PPP 中载波相位的权重远大于伪距，但如果伪距的质量太差依然会影响对位置、模糊度参数的准确估计.图6 绘制了GPS、BDS、GLONASS 三个系统的载波相位、伪距的残差以及对应的高度角图.从图6 中可以看出，载波相位测量值的残差在±0.1 cm 内波动，伪距测量值在±5 m 内波动；并且可以看到伪距和载波相位的残差值在飞机起飞和降落阶段波动较大，在飞行过程中保持稳定，主要原因是飞机起飞和降落时环境变化较大，测量误差较大.从图中也可以看出，BDS-2 的卫星高度角大部分在30°以上，且50°以上占比较大，GPS 的卫星高度角集中在10°～40°，50°以上占比较小，这与BDS-2 在亚太地区的可视卫星数较多有关，BDS-2 相对更大的卫星高度角测量会使得多路径造成的误差更小.

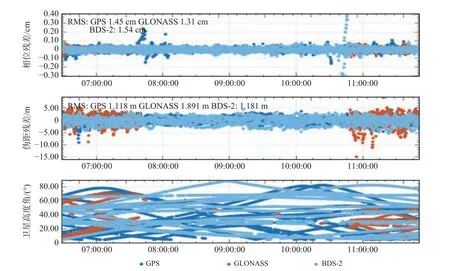
图6 观测值残差以及卫星高度角

根据实测数据计算出GPS、BDS、GLONASS 的载波相位测量值残差分别是1.45 cm、1.54 cm 和1.31 cm，伪距测量值残差分别为1.118 m、1.181 m和1.891 m，三个卫星导航系统的载波相位观测值残差相近，相差10～20 mm，但对于伪距观测值残差，GPS 最小，GLONASS 最大，GPS 与BDS 伪距测量残差相近，在1.15 m 附近，GLONASS 较之降低了约60%.从测量残差来看，BDS 的观测值残差与GPS 接近，均低于GLONASS 的观测值残差，因此从残差来看，BDS 和GPS 的观测质量相近，GLONASS 的观测质量较差.

3.3 定位精度分析

图7 为单GPS、单BDS-2、BDS-2+GPS 以及BDS-2+GPS+GLONASS 的定位精度序列，表2 为不同组合系统下的平均定位精度.定位序列在飞机起飞和降落时有明显的抖动，在U 方向尤其明显，推测是对流层模型剧烈变化导致结果估计不稳定.从表2 中可以看出，无论是单GPS、单BDS 还是组合系统GPS+BDS 以及GPS+BDS+GLONASS，其动态PPP 在东(E)方向和北(N)方向的定位精度都要远优于U 方向的定位精度，一方面是因为处于平面方向的卫星分布较均匀，卫星空间几何构型较好，而只有U 方向有卫星分布，几何构型较差；另一方面，由于电离层延迟、对流层延迟等误差改正项主要是投影到U 方向，对于定位的精度影响较大，从表2 中也可以看出，E 方向和N 方向的平均精度高于U 方向60%～90%.

图7 不同组合下的定位精度

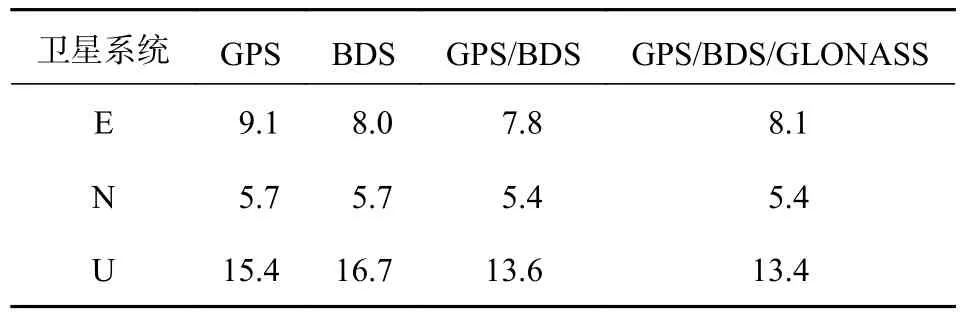
表2 不同组合下的定位精度 cm

同时单BDS 的PPP 在E 方向和N 方向较单GPS 精度更高，GPS+BDS 的PPP 在E、N 和U 方向上均优于单GPS 和单BDS，其中在U 方向提升更为明显.我们也可以发现GPS+BDS+GLONASS 与GPS+BDS 的定位表现相近，主要是由于GLONASS 卫星在飞机起飞后可视卫星数目急剧减少，对结果的贡献很小.这与图4 中可用卫星数也可以看出来总卫星数在飞行阶段与GPS+BDS 的基本一致.因此多系统PPP 相比单系统PPP 而言，能提高定位的精度.

3.4 PRIDE PPP-AR 软件与WayPoint 软件结果对比

图8 中我们将PRIDE PPP-AR 的解算结果同WayPoint 差分解做了比较.

图8 WayPoint 软件基线解

可以看到在飞机起飞后图中水平方向和U 方向表现出明显的“阶跃”，推测是由于模糊度固定错误导致的位置跳变.最终，定位结果在三个方向定位精度分别达到了13.3 cm、15.4 cm、18.6 cm，WayPoint 的解算精度相比PRIDE PPP-AR 而言，GPS+BDS 的PPP在E 方向和U 方向分别降低了46%和36%，N 方向下降最多，降低了近2 倍.因此PRIDE PPP-AR 软件的PPP 解算结果显著优于WayPoint 软件的解算结果.

4 结束语

本文通过机载NovAtel GPScard 接收机在海南省所进行的动态PPP 实验，由于GLONASS 在飞机起飞后卫星数急剧减少，对解算结果贡献比较小，因而本文主要是利用PRIDE PPP-AR 软件进行了单GPS、单BDS、GPS+BDS 以及BDS+GPS+GLONASS的动态PPP 解算.结果表明：

1)相比GPS，单BDS-2 在亚太地区拥有更多的可视卫星，平均10～15 颗，因此具有更好的几何构型.从定位结果来看，单BDS-2 动态PPP 定位精度在E、N、U 三个方向分别为8.0 cm、5.7 cm、16.7 cm，相比单GPS 结果在E 方向提高了12%.如果引入BDS-3卫星，定位性能会得到进一步提升.

2)机载动态情况下多系统GNSS 的PPP 在实际解算中优势更为明显，其可视卫星数更多，卫星几何构型更好；E、N、U 方向的定位精度都高于单系统，U 方向提升更加明显，在U 方向上，GPS+BDS 比单GPS、单BDS 精度提升了12%和19%，这对于高程方向更加敏感的应用场景如航空重力测量会更有帮助.

3)本文利用PRIDE PPP-AR 软件的动态PPP 解算结果与WayPoint 软件差分解对比，结果表明PRIDE PPP-AR 解算结果精度相比前者在E 和U 方向分别提高了46%和36%，N 方向提高了近两倍，因此其解算结果显著优于WayPoint 软件的解算结果，且前者完全开源，而后者为商业软件，因此PRIDE PPP-AR 软件相比WayPoint 软件具有更加显著的解算性能与应用能力.

致谢：感谢武汉大学PRIDE Lab 提供的开源软件PRIDE PPP-AR 的支持.感谢中国自然资源航空物探遥感中心提供的机载观测数据.