BDS-2/BDS-3/GPS/Galileo 双频精密单点定位精度分析与评价

卢福康，余学祥，肖星星，胡富杰

(1.安徽理工大学 空间信息与测绘工程学院,安徽 淮南 232001；2.安徽理工大学 矿区环境与灾害协同监测煤炭行业工程研究中心,安徽 淮南 232001；3.安徽理工大学 矿山采动灾害空天地协同监测与预警安徽普通高校重点实验室,安徽 淮南232001)

0 引言

随着全球卫星导航技术的快速发展，卫星定位技术已成为空间信息技术基础设施不可或缺的部分.在国民经济建设，尤其在现代化军事建设方面发挥着十分重要的作用，也是一个国家在国际地位的重要体现，而北斗卫星导航系统(BDS) 已成为全球卫星导航系统(GNSS)中重要的组成部分.BDS 是我国自行研制的卫星导航系统，BDS 的发展战略为“三步走”战略：由最初的北斗卫星导航试验系统(BDS-1)到北斗二号卫星导航系统(BDS-2)最后北斗三号全球卫星导航系统(BDS-3)[1-5].2020 年6 月我国BDS-3 正式组网的卫星发射成功，BDS-3 由30 颗卫星组成，主要包括3 颗倾斜地球轨道同步(IGSO)卫星，3 颗地球静止轨道(GEO)卫星和24 颗中地球轨道(MEO)卫星组成，新增加了4 个信号，包括B1C 信号(1 575.42 MHz)、B2a 信号(1 176.45 MHz)、B2b 信号(1 207.14 MHz)和B2a+b (1 191.79 MHz).相信未来BDS-2 和BDS-3将一起为中国提供高精度定位服务，甚至将为全球提供定位服务[6-9].

随着我国BDS 的迅速发展，针对BDS 的定位性能已经有大量学者对其进行了研究.文献[10] 对BDS-2 与BDS-3 进行静态精密单点定位(PPP)分析，东(E)、北(N)、天顶(U)三个方向的定位精度分别为1.07 cm、1.95 cm、2.04 cm；加入BDS-3 后，相对BDS-2 提升了27.15%、27.87%、35.76%.文献[11]对BDS-3 进行实时静态PPP，N 方向上优于1 cm，E 方向和U 方向上同时优于1～4 cm，与BDS-2 相比，水平和高程分别提升了50.23%、60.24%.文献[12] 对比分析了 BDS+Galileo+GPS 单频 PPP 精度性能，该组合系统动态单频PPP 性能最优在系统偏差采用1 h分段常数模型时，N、E、U 各个方向的收敛精度分别为5 cm、5 cm、11 cm；文献[13]通过对BDS-2/BDS-3 PPP 的数据处理理论与方法进行了深入研究，得出了BDS-2/BDS-3 的最佳处理方案；文献[14]对BDS-2/BDS-3 融合静态PPP 在E、N、U 方向上的定位精度和收敛时间分别为1.2 cm、1.0 cm、1.8 cm 和15.8 min、7.3 min、22.3 min.以上大都是对单系统的研究，对以BDS-2/BDS-3 为主体的研究较少，本文通过对比无电离层组合模型对BDS-2/BDS-3、BDS-2/BDS-3/GPS、BDS-2/BDS-3/Galileo 及BDS-2/BDS-3/GPS/Galileo 进行PPP 静态精度评估与分析.

1 PPP 定位基本函数模型

采用原始伪距和载波相位观测值结果可以表示为：

式中：s、r 为卫星和接收机；j(j=1，2，3)为信号频率；p、L分别为原始伪距和载波相位观测值，单位为m；ρ为卫星到接收机之间的几何距离；dtr、dts分别为接收机钟差和卫星钟差；Tw为对流层天顶延迟(ZTD)及其对应的映射函数为电离层延迟及其对应的放大影响因子 γj，其中分别为接收机未校准的码延迟(UCD)和未校准的相位延迟(UPD)，单位为m；分别为卫星未校准的码延迟(UCD)和未校准的相位延迟(UPD)；分别为原始伪距和载波相位观测值的观测噪声；此外，式(1)中的其他误差项，如相位缠绕、天线相位中心改正等均使用相应模型进行改正.

为方便起见，将无电离层组合的系数定义为

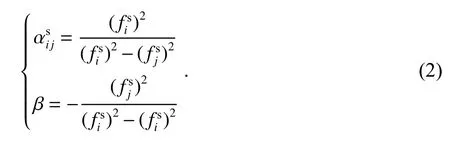
一般来说，国际GNSS 服务(IGS)卫星时钟产品是通过使用第一和第二频率的无电离层组合观测而产生的.因此，卫星时钟吸收了无电离层的卫星UCD，则无电离层的卫星时钟误差被定义为

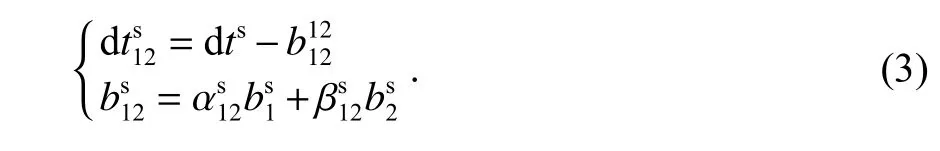
1.1 无电离层组合模型

双频无电离层PPP 模型中的估计参数包括接收机位置、时钟偏移量、天顶对流层湿延迟、相位模糊度.通过采用两个频率间的伪距和载波相位观测值分别进行组合成无电离层组合，其公式形式为[15]

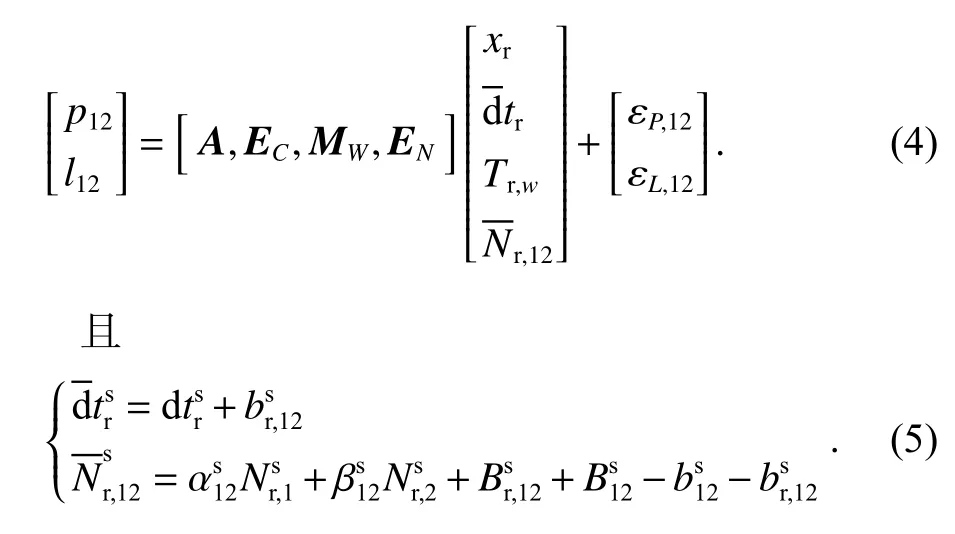
式中：p12、l12分别对应无电离层的伪距和相位观测值；是无电离层的浮点模糊度；A是坐标向量xr的设计矩阵；EC是一个n×m的矩阵，其中每个元素都是1，其中n代表n颗卫星，m代表m个系统，dtr是对应的GNSS 接收机钟差；MW是一个n维的列向量；EN是对应的模糊度的n×n维矩阵；εP,12、εL,12为观测值对应的噪声，其他相同元素含义同式(1).

1.2 随机模型

在对GNSS 进行PPP 定位时，不仅要考虑函数模型，还要考虑随机模型，在PPP 中运用比较常用的是高度角随机模型和信噪比随机模型.其中，高度角模型是指构建高度角E和测量噪声 σ2之间的函数关系式，其通用公式为

式中：E为卫星高度角；a和b是常数，值均为0.003.

2 数据来源和处理策略

基于BDS-3 正式组网完成，为了进一步研究BDS PPP 的定位性能，本文的实验数据是采取MGEX(Multi-GNSS Experiment)中心下载到的观测数据，采取的数据是8 个测站5 天的观测数据，测站图如图1所示，其他的精密星历产品和精密钟差产品均来自武汉大学IGS 中心.

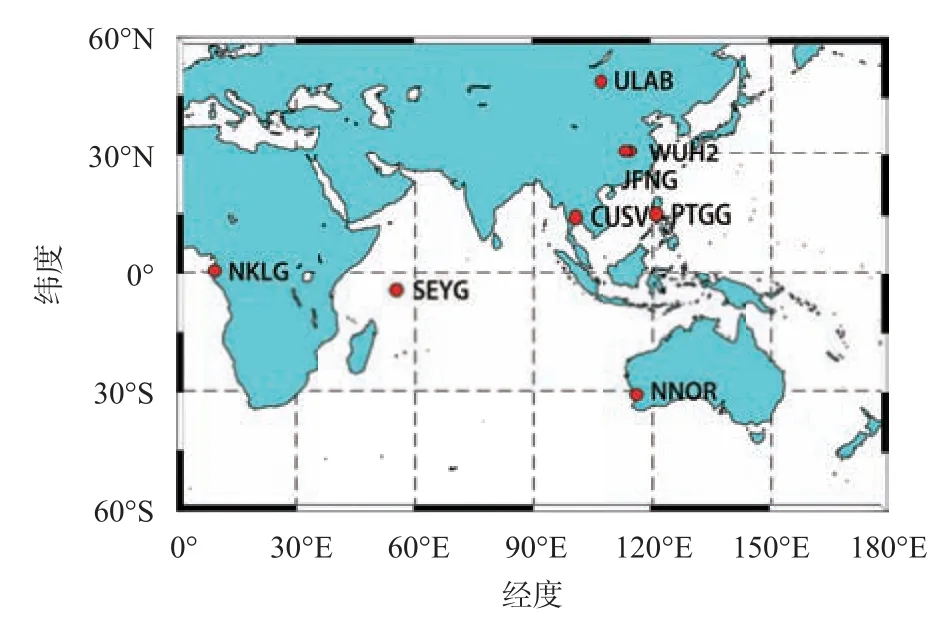
图1 8 个MGEX 测站分布图

在数据处理过程中，对于精度验证是文中解算定位结果与IGS 提供的snx 文件周解值比较，然后分析N、E、U 三个方向上的定位精度及收敛时间，收敛时间是根据三维方向定位误差达到0.1 m 误差已内并达到稳定至少有30 个历元所需要的时间，定位精度为三个方向达到0.1 m 并稳定至少有30 个历元的各个方向的误差，若超过0.1 m，则最后的历元为定位的精度.对于接收机钟差的方差设置为1002m2，位置坐标参数方差设置为0 m2，对流层延迟、电离层延迟、接收机的钟差、模糊度参数等由于先验信息未知，初始化设置值为0，对流程层的方差设置为10-8m2，电离层的方差设置为10-4m2，PPP 主要的处理策略如表1 所示.

表1 PPP 处理策略

为了评估以BDS-2/BDS-3 为主体的组合卫星系统的定位性能，主要分为四种评估方案：BDS-2/BDS-3、BDS-2/BDS-3/GPS、BDS-2/BDS-3/Galileo、BDS-2/BDS-3/GPS/Galileo 四种组合的无电离层组合模型的静态PPP 定位精度和收敛时间评定.

3 实验结果分析

3.1 BDS-2/BDS-3 卫星系统静态PPP 性能分析

卫星可见数也是影响定位精度高低的一个重要因素，BDS-2/BDS-3 卫星可见数如图1 所示.

由图2 可知，BDS-2/BDS-3 的4 个测站每日平均卫星可见数在14～23 颗.根据方案1 对BDS-2/BDS-3 5 天观测数据进行无电离层组合进行静态PPP 处理，将解算出的结果与IGS 下载的已知坐标(真值)进行作差，并统计E、N、U 三个方向的偏差和收敛时间，通过精密度(STD)来反应8 个测站之间误差的离散情况，如式(7) 所示.由于论文结构原因随机选取4 个测站CUSV、PTGG、SEYG、NNOR 站为代表，如图3 所示.8 个测站静态统计结果如表2 所示.

图2 BDS-2/BDS-3 的4 个测站5 天卫星可见平均数

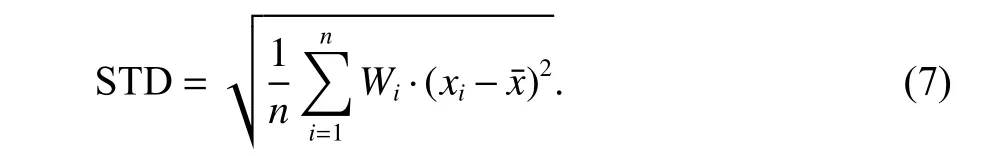
式中：n为观测值个数；Wi为权重；xi为观测值；为观测值平均值.

由图3 和表2 可知，在各个方向的定位精度上，4 个测站在E 方向上平均每天的定位精度比较稳定，分别约为2.0 cm、2.5 cm、2.7 cm、2.4 cm，8 个测站整体的平均精度在2.49 cm，整体精密度为0.34，N 方向上平均每天的定位精度分别约为1.6 cm、1.7 cm、1.5 cm、2.4 cm，整体平均精度在2.27 cm，整体精密度为0.59，U 方向上平均每天的定位精度分别约为3.7 cm、3.6 cm、4.0 cm、3.7 cm，整体平均精度为4.04 cm，整体精密度为0.47；在收敛时间上，N 和U 方向上比E 方向上收敛速度快，整体平均收敛时间分别为34.6 min、19.3 min、28.1 min，整体的精密度分别为9.72、5.2、3.5.

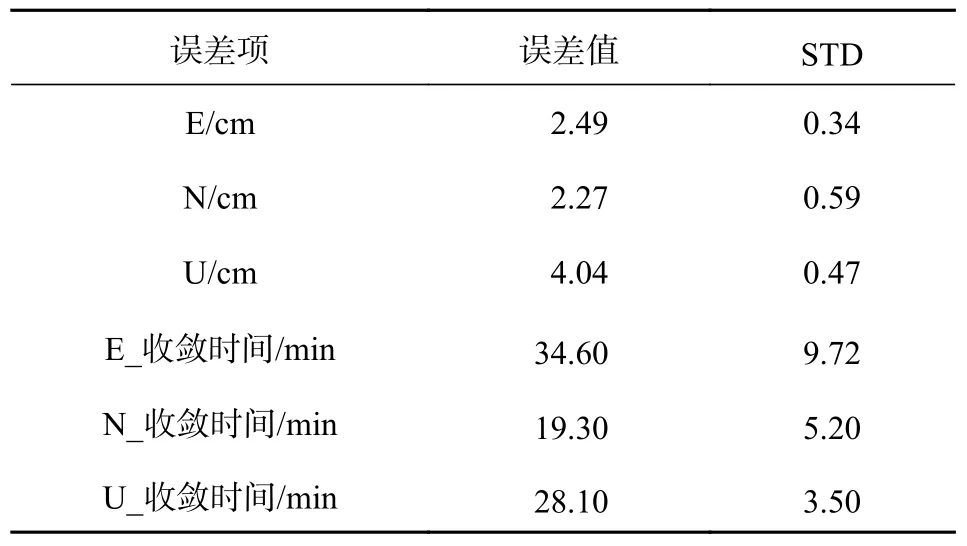
表2 8 个测站静态PPP 统计结果

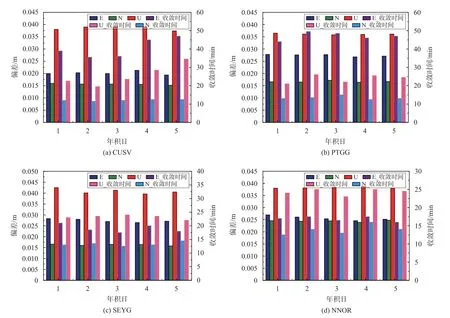
图3 BDS-2/BDS-3 的4 个测站5 天静态PPP E、N、U 方向偏差及收敛时间

3.2 BDS-2/BDS-3/Galileo 卫星系统静态PPP 性能分析

为了更好地分析无电离层组合静态PPP 定位精度和收敛时间，对BDS-2/BDS-3 系统中加入Galileo卫星定位系统进行分析.同样卫星可见数对定位精度和收敛时间占有重要的影响，BDS-2/BDS-3/Galileo卫星可见数如图4 所示.

由图2 和图4 可知，BDS-2/BDS-3 每天平均卫星可见数在14～23 颗，加入Galileo 后有了明显的增加，每天平均卫星可见数在19～31 颗，增加了约8 颗的卫星.组合系统有利于改变卫星空间的几何结构，来提高卫星的定位精度.根据方案2 对BDS-2/BDS-3/Galileo 4 个测站5 天观测数据进行静态PPP 处理，结果如图5 所示，8 个测站静态统计结果如表3 所示.

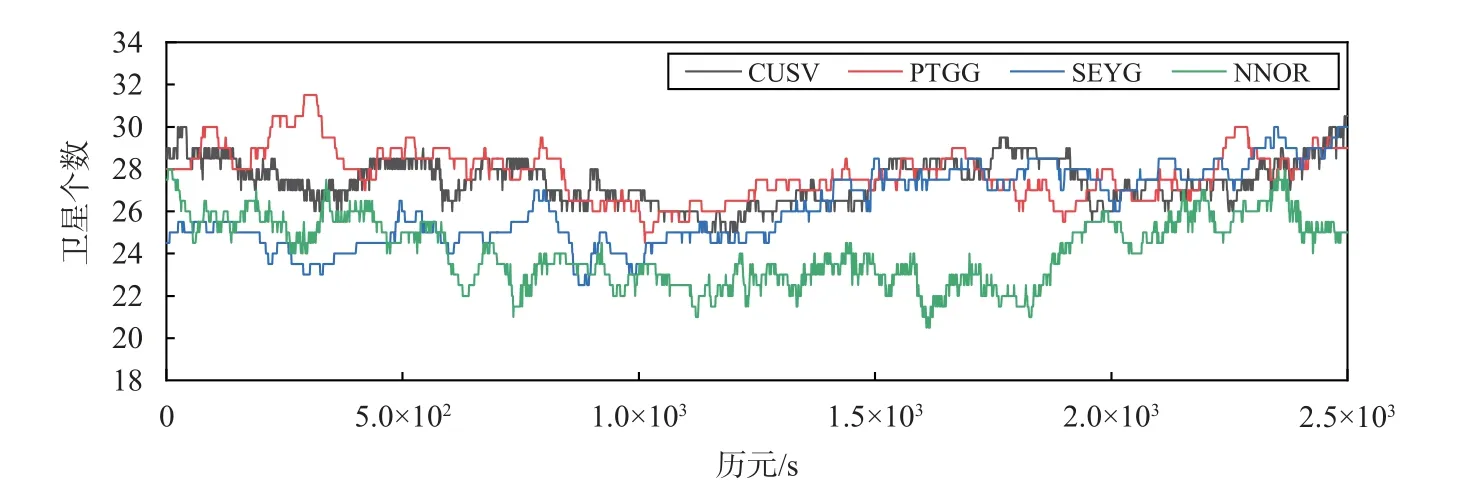
图4 BDS-2/BDS-3/Galileo 的4 个测站5 天卫星可见平均数

由图5 和表3 可知，4 个测站在E 方向上平均每天的定位精度比较稳定，分别约为1.5 cm、2.0 cm、2.1 cm、1.9 cm，8 个测站整体平均精度在1.81 cm，整体精密度为0.25，N 方向上平均每天的定位精度分别约为1.2 cm、1.3 cm、1.2 cm、1.9 cm，整体平均精度在1.65 cm，整体精密度为0.44，U 方向上平均每天的定位精度分别约为3.0 cm、2.7 cm、3.0 cm、2.8 cm，整体平均精度为2.94 cm，整体精密度为0.26；在收敛时间上，N 方向上比E 和U 方向上收敛速度快分别为20.40 min、13.00 min、18.60 min，整体的精密度分别为3.64、3.28、1.84.

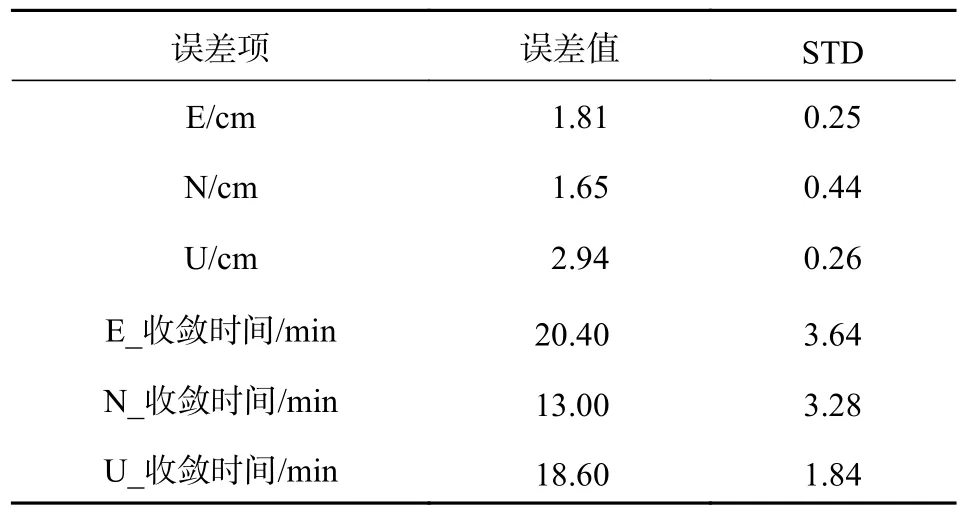
表3 8 个测站静态PPP 统计结果

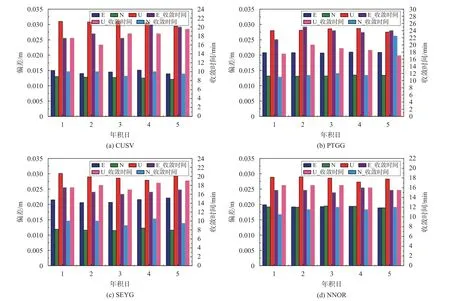
图5 BDS-2/BDS-3/Galileo 的4 个测站5 天静态PPP E、N、U 方向偏差及收敛时间

3.3 BDS-2/BDS-3/GPS 卫星系统静态PPP 性能分析

本小节主要用BDS-2/BDS-3/GPS 组合系统来对无电离层组合来对静态PPP 的性能进行分析，对于卫星的可见数是影响定位精度的重要影响，图6是BDS-2/BDS-3/GPS 的4 个测站5 天卫星可见数平均值.

由图2 和图6 可知，组合系统BDS-2/BDS-3/GPS 比BDS-2/BDS-3 系统卫星可见数明显增多，前者平均约在20 颗，后者平均约在28 颗，比之增加了约8 颗，提高卫星空间的几何结构，以便提高定位精度和收敛时间.根据方案3，通过用无电离层组合和非差非组合两种方法来对组合系统BDS-2/BDS-3/GPS 系统的观测值进行PPP 静态解算，以4 个测站5 天观测数据进行静态PPP 处理为例，如图7 和表4所示.

表4 8 个测站静态PPP 统计结果

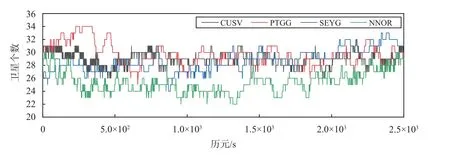
图6 BDS-2/BDS-3/GPS 的4 个测站5 天卫星可见平均数

图7 BDS-2/BDS-3/GPS 的4 个测站5 天静态PPP E、N、U 方向偏差及收敛时间

由图7 和表4 可知，4 个测站在E 方向上平均每天的定位精度比较稳定，分别约为1.4 cm、1.9 cm、2.0 cm、1.6 cm，8 个测站整体平均精度在1.67 cm，整体精密度为0.29，N 方向上平均每天的定位精度分别约为1.4 cm、1.3 cm、1.1 cm、1.6 cm，整体平均精度在1.62 cm，整体精密度为0.42，U 方向上平均每天的定位精度分别约为2.9 cm、2.4 cm、2.8 cm、2.7 cm，整体平均精度为2.82 cm，整体精密度为0.26；在收敛时间方面，N 方向比E 和U 方向收敛速度快分别为18.30 min、10.20 min、16.10 min，整体的精密度分别为3.12、1.84、1.77.

3.4 BDS-2/BDS-3/GPS/Galileo 卫星系统静态PPP性能分析

为了更进一步分析不同组合系统对两种方法PPP 定位性能分析，在之前BDS-2/BDS-3/GPS 组合系统的基础上再加上Galileo 系统进行分析，首先随着系统的增多，使得卫星的可见数大大得到了增加，使得这因素变得更加重要，卫星可见数如图8 所示.

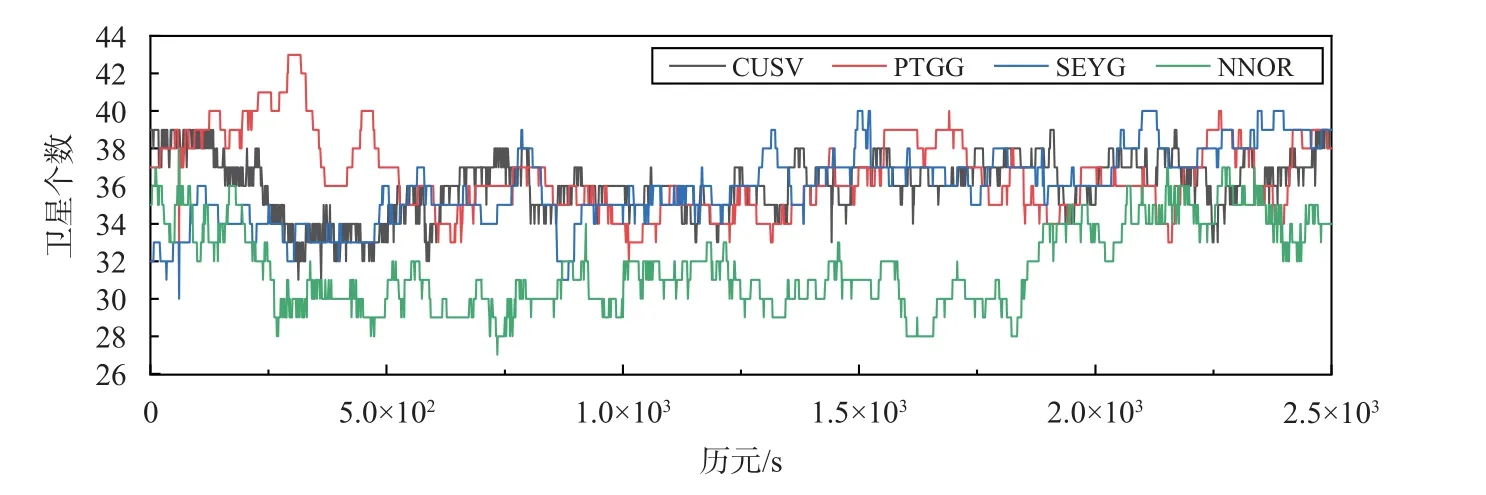
图8 BDS-2/BDS-3/GPS/Galileo 的4 个测站5 天卫星可见平均数

由图2 和图8 可知，组合系统BDS-2/BDS-3/GPS/Galileo 比BDS-2/BDS-3 系统卫星可见数有很大增多，前者平均约在20 颗，后者平均约在37 颗，比之增加了约17 颗，提高卫星空间的几何结构，使其很好的改善了卫星空间分布结构，更加大程度上提高定位精度和收敛时间.根据方案4，对组合系统BDS-2/BDS-3/GPS/Galileo 进行解算来对其定位精度和收敛时间进行分析，以4 个测站5 天观测数据进行静态PPP 处理为例，如图9 所示，8 个测站统计结果如表5所示.

图9 BDS-2/BDS-3/GPS/Galileo 的4 个测站5 天静态PPP E、N、U 方向偏差及收敛时间

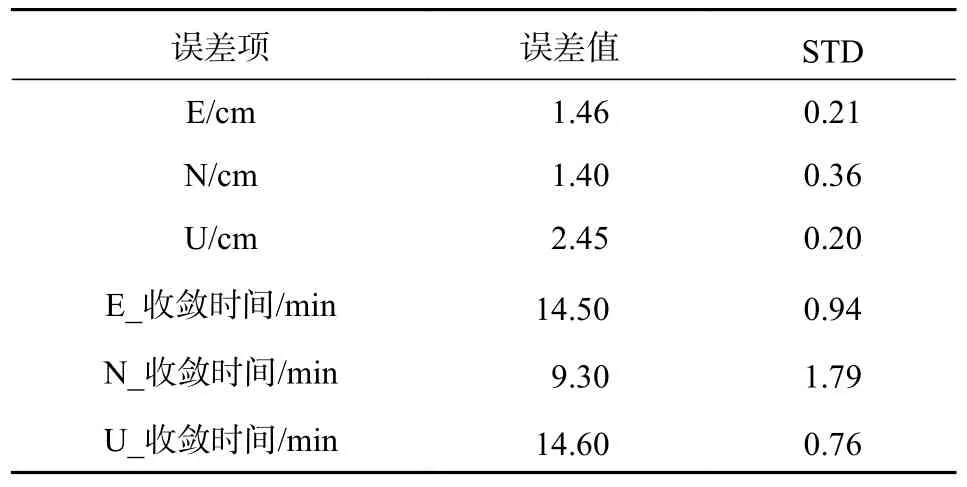
表5 CUSV 站30 天三方向偏差及收敛时间统计结果

由图9 和表5 可知，对4 个测站5 天的定位结果进行分析，在E 方向上5 天每天定位精度的平均值分别约稳定在1.2 cm、1.6 cm、1.7 cm、1.5 cm，8 个测站整体的平均定位精度在1.46 cm，整体精密度为0.21，在N 方向上5 天每天定位精度的平均值分别约稳定在1.2 cm、1.1 cm、1.2 cm、1.6 cm，8 个测站整体的平均定位精度在1.40 cm，整体精密度为0.36，在U 方向上5 天每天定位精度的平均值分别约稳定在2.5 cm、2.4 cm、2.4 cm、2.6 cm，8 个测站整体的平均定位精度在2.45 cm，整体精密度为0.20；在收敛时间方面：各个方向的5 天的平均每天收敛时间都比较稳定，8 个测站整体的平均收敛时间分别为14.5 min、9.3 min、14.5 min，整体的精密度分别为0.94、1.79、0.76.

3.5 四种不同卫星组合系统进行对比分析

为了更好研究和分析不同组合卫星系统间解算结果的定位精度和收敛时间，对8 个测站5 天解算的结果进行统计，结果如图10 和表6 所示.

图10 8 个测站5 天四种不同组合卫星系统定位精度及收敛时间总结直观图

表6 四种不同组合系统定位精度和收敛时间统计表

由图10 和表6 可知，在定位精度方面，BDS-2/BDS-3/Galileo 组合系统与单系统BDS-2/BDS-3 相比，静态PPP 在E、N、U 三方向定位精度分别提升了27.3%、27.3%、27.2%；在收敛时间上，E 方向上提升收敛速度最明显，E、N、U 三个方向收敛速度分别提升了41.0%、32.6%、33.8% ；BDS-2/BDS-3/GPS组合系统与单系统BDS-2/BDS-3 相比，在E 方向上提升最明显，E、N、U 定位精度分别提升了32.9%、28.6%、30.1%；在收敛时间上，各个方向E、N、U 收敛速度分别提升了47.1%、47.2%、42.7%；BDS-2/BDS-3/Galileo/GPS 组合系统与单系统BDS-2/BDS-3 相比，静态PPP 在E、N、U 各方向定位精度分别提升了41.3%、38.3%、39.3%；在收敛时间上，E、N、U 三方向上收敛速度分别提升了58.3%、51.8%、48.3%；对组合卫星系统BDS-2/BDS-3/Galileo 与BDS-2/BDS-3/GPS 相比，两者的各个方向的定位精度相当，E 方向上定位精度都约在1.7 cm，N 方向上约在1.6 cm，U 方向上约在2.8 cm；在收敛时间上，后者比前者在E、N、U 三方向上收敛速度分别提升了10.2%、21.5%、13.4%；双系统BDS-2/BDS-3/Galileo、BDS-2/BDS-3/GPS 与三系统BDS-2/BDS-3/GPS/Galileo 相比，三组合系统精度更高一点，在定位精度方面，后者比前者在E、N、U 三方向上分别提升了(19.3%、12.5%)、(15.1%、13.5%)、(16.6%、13.1%)；在收敛时间上，三系统组合比双系统组合在E 方向上收敛速度分别提升了10.2%、20.7%，N 方向上分别提升了28.4%、8.8%，U 方向上分别提升了22.0%、9.9%.

4 结论

BDS 已正式组网完成，为了进一步研究BDS 的性能，用两种不同的函数解算模型进行评估，本文通过MGEX 8 个测站5 天卫星实测数据先对BDS-2/BDS-3 组合系统进行静态PPP 定位精度和收敛时间进行性能评估，再对双组合系统BDS-2/BDS-3/GPS和BDS-2/BDS-3/Galileo 进行静态PPP 定位精度和收敛时间进行性能评估，最后对三组合系统BDS-2/BDS-3/GPS/Galileo 进行静态PPP 定位精度和收敛时间进行性能评估，试验结果表明：

1)双系统组合BDS-2/BDS-3/GPS、BDS-2/BDS-3/Galileo 和三系统组合BDS-2/BDS-3/GPS/Galileo 的每日的平均卫星可见数比BDS-2/BDS-3 系统有了明显的提升，这样有利于改善卫星的空间分布结构，对定位精度和收敛时间有了提升.

2)对不同组合的卫星系统而言，BDS-2/BDS-3/Galileo、BDS-2/BDS-3/GPS双组合系统与BDS-2/BDS-3单系统相比，在E、N、U 方向上定位精度分别提升(27.3%、27.3%、27.2%)、(32.9%、28.6%、30.1%)；BDS-2/BDS-3/Galileo 和BDS-2/BDS-3/GPS 两个双组合系统定位精度相当；BDS-2/BDS-3/GPS/Galileo 三组合系统与BDS-2/BDS-3 单系统相比，在E、N、U 方向上定位精度分别提升了(41.3%、38.3%、39.3%)；BDS-2/BDS-3/GPS/Galileo 三组合系统与BDS-2/BDS-3/Galileo、BDS-2/BDS-3/GPS 双组合系统相比，在E、N、U 方向上定位精度分别提升了(19.3%、15.1%、16.6%)、(12.5%、13.5%、13.1%).

3)对不同组合的卫星系统而言，BDS-2/BDS-3/Galileo、BDS-2/BDS-3/GPS 双组合系统与BDS-2/BDS-3 单系统相比，在E、N、U 方向上收敛速度分别提升(41.0%、32.6%、33.8%)、(47.1%、47.2%、42.7%)；BDS-2/BDS-3/Galileo 和BDS-2/BDS-3/GPS 两个双组合系统收敛速度相差不大；BDS-2/BDS-3/GPS/Galileo三组合系统与BDS-2/BDS-3 单系统相比，在E、N、U 方向上定位精度分别提升了(41.3%、38.3%、39.3%)；BDS-2/BDS-3/GPS/Galileo 三组合系统与BDS-2/BDS-3/Galileo、BDS-2/BDS-3/GPS 双组合系统相比，在E、N、U 方向上定位精度分别提升了(10.2%、28.4%、22.0%)、(20.7%、8.8%、9.9%).