基于GNSS TEC 的电离层自相关预报误差分析及参数优化

熊雯，王博文，刘裔文,3，朱庆林

(1.中国电波传播研究所,山东 青岛 266107；2.南昌大学 信息工程学院,南昌 330031；3.上饶师范学院 物理与电子信息学院,江西 上饶 334001)

0 引言

电离层电子密度的变化是影响无线电系统工作性能的重要误差源之一，对电离层总电子含量(TEC)进行预报是减缓电离层误差的主要途径.尤其对全球卫星导航系统(GNSS) 应用具有重要使用价值.例如，对GNSS 单频用户，TEC 预报是有效减缓电离层延迟误差影响的重要途径.另外，电离层预报也是提高基于GNSS 信标观测的全球电离层地图(GIM)精度的重要手段.

从预报时间提前量的角度看，电离层预报模型可分为长期预报模型和短期预报模型.长期预报模型一般是太阳活动指数或地磁活动指数驱动，能反应电离层周日、季节、11 年周期变化等大尺度变化的全球性模型，例如国际参考电离层模型、NeQuick 模型等.短期预报模型通常基于临近的历史观测数据的建模来预测当地未来1～24 h 的结果.因短期预报具有较高的区域预测精度，且效率高，故常被用于一些对时效性和精度要求较高的导航、通信、雷达等系统的电离层延迟修正.

早在2000 年左右，就有学者提出了一些有效的短期预报方法，例如自相关方法、自回归方法和人工神经网络等[1-3].目前，工程上用的较多的是自相关或自回归方法[4-8].制约电离层短期预报精度的主要因素主要是磁暴、亚暴等引起的电离层扰动和平静期电离层存在的一些局地小尺度扰动.这些扰动的变化很复杂，至今依然是研究的热点，目前还很难对其进行准确预报.总的来说，对于电离层短期预报，至今并没有一种绝对优势的方法，寻求对已有传统方法进行优化仍然是提高预测精度的重要途径之一[9-11].

自相关预报是一种模型简单且精度较高的预报方法，本文针对自相关预报方法中的参数设置对误差的影响进行深入分析，进而提出优化方案.首先介绍所使用的数据和处理方法，其次介绍自相关预报原理和方法，在再次比较自相关与自回归方法的基础上，开展误差分析和参数优化分析；最后进行讨论和总结.

1 数 据

本文研究所采用的数据主要来自麻省理工大学CEDAR Madrigal 数据库，其数据来自于分布全球的地基卫星接收机网络(Distributed Ground Based Satellite Receivers)中的GNSS 接收机网络(World-wide GNSS Receiver Network) (http://cedar.openmadrigal.org/list).

Madrigal 收集的TEC 测量值均为垂直TEC，单位为TECU，1 TECU 表示每平方米有1016个电子.垂直TEC 是由斜TEC 通过电离层薄层假设(高度为350 km)转换得到.最后通过格网化高精度TEC 地图重构算法生成并提供1°×1°×5 min 时空分辨率的全球垂直TEC 地图[12].

但是，Madrigal 数据库并没有直接提供单站垂直TEC 数据.为开展单站电离层预报方法研究，本文在全球TEC 地图中从观测站网密集区域任意选取了5 个格网点的TEC 数据，然后通过1 h 平均得到单站垂直TEC 日变化时间序列，以此作为本文的实测TEC 时间序列.图1 给出了所选取的5 个网格点分布图.图1 中5 个网格点的坐标分别为：1(45°N，120°W)；2(30°N，105°W) ；3(40°N，90°W) ；4(30°S，25°E)；5(28°N，85°E).

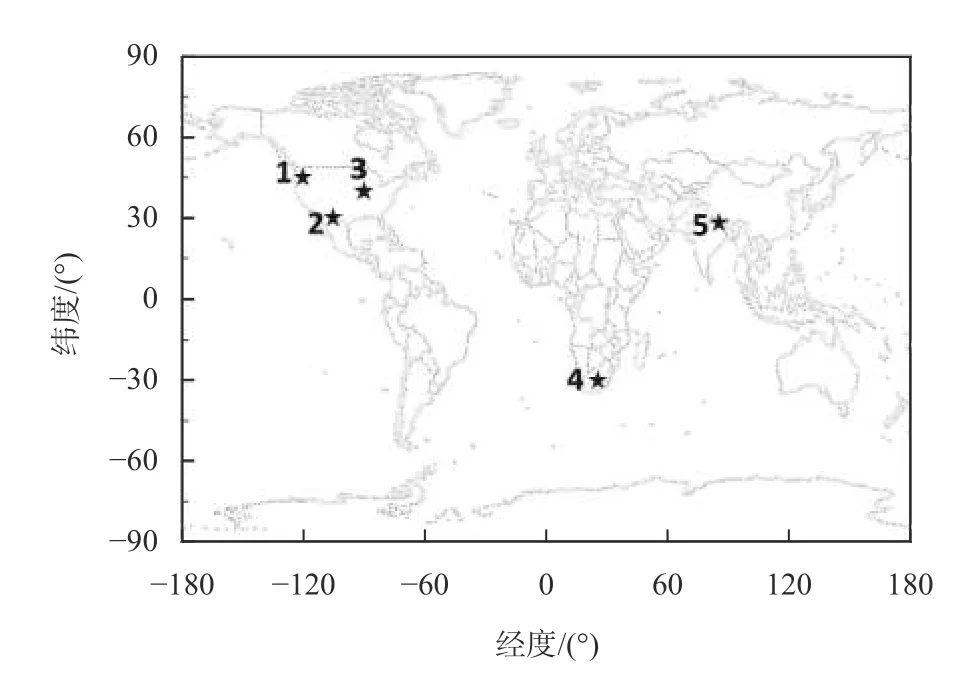
图1 选取的5 个网格点坐标示意图

2 自相关预报原理和方法

在1 个月左右的时间尺度上，电离层参量的时间序列通常是平稳时间序列，在统计学上可将其视为具有非零自相关函数的随机稳态过程的实现[1].假设某电离层参量小时值的时间序列为z(t)，其在t时刻的值可表示为前n个测量值的加权平均，如式(1)所示：

式(1)中的加权系数 λj通过以下方程组求解得到：

式中：µ 为拉格朗日系数；ρ(τ) 为z(t) 的自相关系数，其均值为0.对于1 h 分辨率的电离层时间序列，引入式(3)所示的拟合函数来进行加权系数的估计[1].

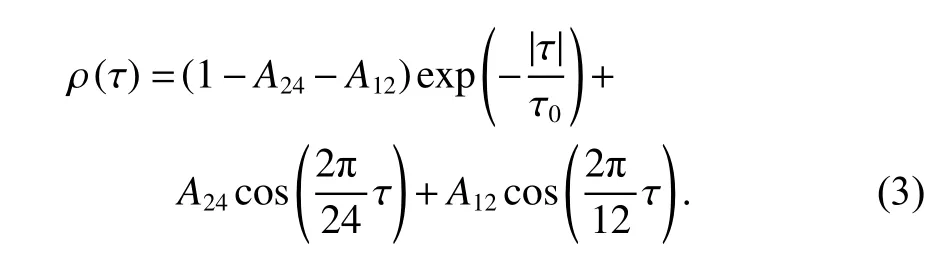
上述处理是从信号的角度将电离层参量的时间序列看成是一个周期信号叠加一个非周期性的扰动.对于周期性信号，我们熟知电离层受日照影响存在明显的周日变化，根据周期信号的傅里叶级数理论，将自相关系数的周期成分用周期为24 h 的基波和2 次谐波的和来表示.而对于非周期的扰动信号，式(3)实际采用的是一个幅度受限的双边指数信号来模拟其变化，其中 τ0是时间常数.式(3)中的三个系数A24、A12、τ0通过最小二乘法来确定，然后，选取最近4 天的12 个最大的自相关系数代入式(2)求解，即可得到对应所选时间的权重系数λj[1].最后，将权重系数代入式(1)即可得到t时刻的预测值.

3 结果

3.1 自相关与自回归预报方法比较

电离层TEC 观测序列是一种典型的周期性时间序列，根据时间序列预测理论，对于数据量较少的情况，通常采用自相关或自回归模型进行预报.本文首先对两类模型进行了比较，自回归模型选用了常用的ARIMA 模型.图2 给出了一个结果示例，所用数据为网格点5 的数据，预报时间为2020 年2 月1 日至2 月10 日.从图2 可以看出，自相关和ARIMA 预报结果均与观测结果吻合较好，很好地再现了电离层TEC 的周日变化特征.

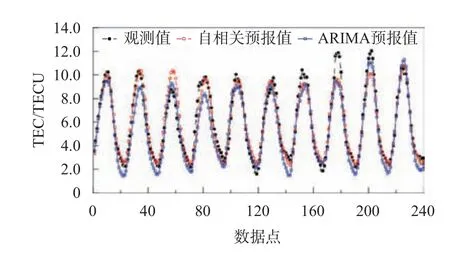
图2 自相关与自回归预报方法结果比较示例

进一步地，我们采用均方根偏差(RMSE)和归一化均方根偏差(NRMSE)来衡量预报绝对误差和相对误差，计算公式为：

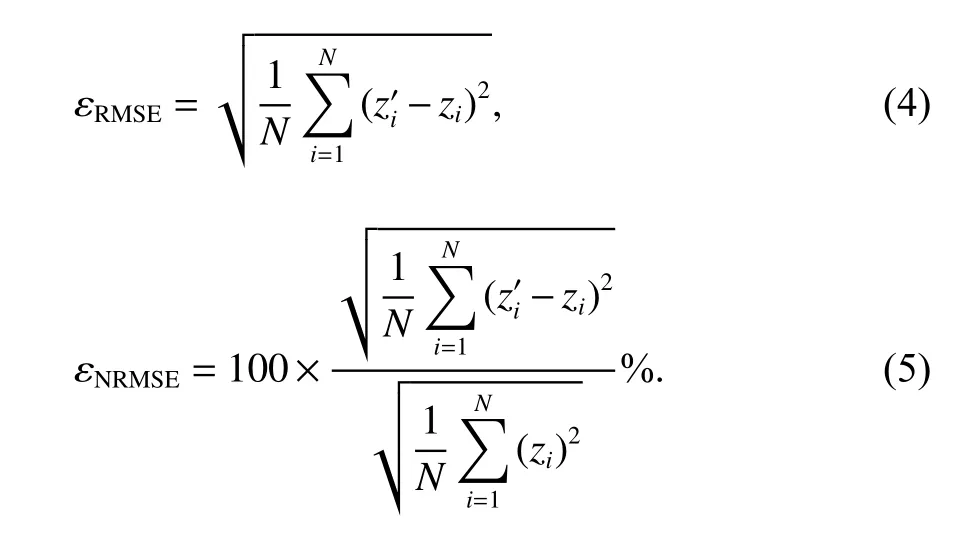
上两式中：εRMSE和 εNRMSE分别为均方根偏差和归一化均方根偏差；和zi分别为第i个点位的预测值和观测值；N为总的点位数.

经估算，图2 所示结果中，自相关预报的绝对误差约为0.716 5 TECU，相对误差约为10.87%；ARIMA预报绝对误差和相对误差分别为0.876 2 TECU 和13.29%.此外，我们还利用网格点1～4 的数据对两种方法进行了比较分析，计算结果显示，对于网格点1～4，自相关方法的绝对误差分别为0.414 5 TECU、0.654 3 TECU、0.515 2 TECU、1.182 1 TECU，ARIMA方法绝对误差分别为0.436 9 TECU、0.607 8 TECU、0.522 6 TECU、1.230 1 TECU；自相关方法的相对误差分别为8.3%、9.52%、8.52%、13.28%，ARIMA 方法相对误差分别为8.75%、8.84%、8.64%、13.82%.

从上述结果对比可以看出，总体上自相关方法的绝对误差和相对误差均略小于ARIMA 方法.此外，我们还对两种预报方法需要花费的时间进行了测算.结果显示，预报如图2 所示的10 天结果，在相同的计算环境下，自相关预报时间约为10 s，ARIMA 预报时间约为50 s.还需指出的是，本文采用的ARIMA 模型使用之前已经定好了阶数，后续的预测均使用固定阶数，若采用动态自动定阶，则预报时间将大大增加.

综上分析，自相关预报方法预报误差相对略优于ARIMA 方法，且自相关预报所需时间比ARIMA少得多.因此，本文后续将主要分析自相关方法.如前所述，自相关方法虽然已经取得了一些应用，但其依然有改进的空间，3.2 小节将在误差分析的基础上尝试对自相关方法进行参数优化.

3.2 自相关误差分析和参数优化

对于自相关预报方法，在预报参数选取方面，目前普遍的做法是，选取最近4 天相关系数最高的12 个时间点，然后通过式(2)解出相应的权重系数.由于这两个参数是早期经验值，其对预报误差的影响目前还没有文献公开报道.为弄清楚这一影响，我们对具体预报过程和误差产生原因进行了深入分析.

图3 给出了参数选取4 天和12 点时的一个预报结果示例.图3 中的TEC 数据来自网格点4 (30°S，25°E)，预测日期为2020 年2 月8 日，所用的历史数据为2020 年1 月9 日至2 月7 日共30 天数据，分辨率为1 h.图3 中黑色圆点表示实测值，2 月8 日的红色圆点表示预测值.我们以第8 个预测点(如图中黑色箭头所指)为例，给出了用来计算该点预测值的历史数据分布(如图中蓝色圆圈所示)，同时在每个历史点位左侧标出了权重系数.根据自相关预测理论，所选取的12 个采样点是前4 天相关系数最大的采样点，这些点主要是前4 天相同时刻和相邻时刻的采样点，且相同时刻的权重最大(为0.093)，而相邻时刻采样点的权重均为0.079.

图3 2020 年2 月8 日“4+12”参数方案时的预报结果(红色圆点)以及2 月4 至8 日实测结果(黑色圆点)

对比图3 中2 月8 日的预报结果和实测结果可以看出，虽然两条曲线的变化趋势基本一致，但几乎所有点位的预测值均要大于观测值.对黑色箭头所示第8 个点位，其观测值为9.264 TECU，预测值为10.292 TECU，误差达到1.029 TECU.从第8 个预测点所用历史点位信息来看，距离预测点最远的2 月4 日的两个被选用的点位对误差影响较大，这两个采样点数值明显高于2 月5 日至2 月8 日其他点位的值，很可能是造成该点预测值明显偏离实测值的主要原因.

图3 结果反映出距离预测点较远的历史数据可能与当前时刻观测值的偏差较大，从而影响预报精度.据此，我们推测，缩短参与预报的历史数据天数，有可能能够减少预报误差.因此，我们将参与预测的天数减少为3 天，相应的点数减为9 个，对上述选例重新开展自相关预测，结果如图4 所示.由图4 可知，整体上，修改参数后的预测值与观测值更接近.对黑色箭头所示第8 个点位，其观测值为9.264 TECU，预测值为9.863 TECU，误差减小为0.599 TECU.

图4 2020 年2 月8 日“3+9”参数方案时的预报结果(红色圆点)以及2 月4 至8 日实测结果(黑色圆点)

此外，我们还分析了天数增加或减小时的结果，图5 给出了不同参数设置下的所有24 个点位预测误差曲线比较，图5 中黑色圆圈代表参数设置为“4+12”时的误差曲线(对应图3 所示结果)，红色圆圈代表参数设置为“3+9”时的误差曲线(对应图4 所示结果).对比上述两条误差曲线可以看出，除12 UT、13 UT、14 UT 三个点位外，其余点位的预测误差都有所减小，尤其是10 UT 之前的点位减少更明显.总体上，原方法“4+12”平均绝对预报误差为0.8 TECU，参数调整为“3+9”后平均绝对预报误差为0.63 TECU，平均绝对误差减小了0.17 TECU.此外，图5 还给出了参数设置分别为“5+12”(紫色圆圈)和“2+6”(绿色圆圈)时的预报误差曲线，但是从对比结果看，两种方案均存在误差明显增加的点位，而误差减少的点位较少.经估计，图5 中“5+12”案的平均绝对误差为0.885 TECU，“2+6”方案的平均绝对误差为0.892 TECU，相对于原方法“4+12”误差还分别增加了0.085 TECU和0.092 TECU.

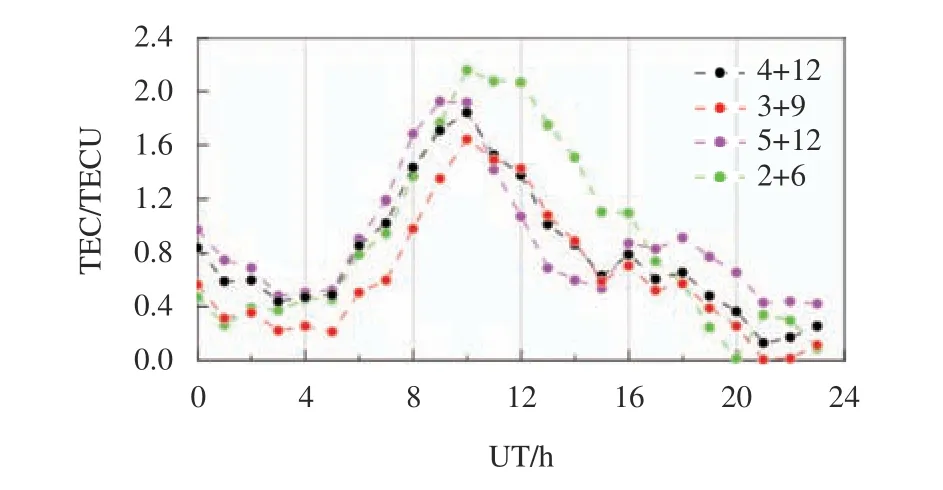
图5 2020 年2 月8 日不同参数方案预报误差比较

上述结果表明，在TEC 自相关短期预报方法中，参与预测的天数设置为3 天(相应的点位设置为9)可能是更优的方案.这从侧面说明电离层当前的状态可能主要取决于前3 天的状态，或者说前3 天的电离层状态对当前状态的关联最大.时间跨度越大，关联性越小，引起误差的可能性越大.

为进一步检验“3+9”参数方案的预报精度改善效果，我们对图1 中所有5 个观测点的数据进行了分析，且每个观测点从2 月1 日至3 月1 日进行30 次1～24 h 短期预报.对每个观测站，我们利用30×24 个时间点的观测值和预测值来计算该站的均方根误差(RMSE)和归一化均方根偏差(NRMSE)，以进行两种参数设置方案的误差比较.两种方案的综合误差比较结果如表1 所示.从表1 结果可以看出，对于本文随机选取的5 个观测站，“3+9”综合预报误差均要优于“4+12”方案.将5 个观测站误差值求平均值可得，所有站RMSE 平均值从0.825 TECU 降低至0.805 TECU，降低了0.02 TECU，NRMSE 平均值从11.756%降低至11.452%，降低了约0.3%.需要指出的是，由于本文所选用TEC 数据的取值水平较低，所以改进效果从绝对值上看较小，但本文经过一定规模的统计分析显示所有站点均有一定改进，因此我们认为这一改进方案是依然有一定参考价值的.

表1 不同观测站两种方案预测误差综合比较

4 结果与讨论

本文首先比较了自相关和自回归滑动平均(ARIMA)方法，结果显示两种方法均能较好地预测TEC周日变化.对本文预报结果进行了RMSE 和NRMSE估算，结果表明总体上自相关预报误差略低于ARIMA预报误差，且在相同计算环境下，自相关预报所花费的时间明显少于ARIMA 模型.

其次，本文对自相关预报方法的误差进行了深入分析，重点分析了实际参与加权的观测值覆盖天数和观测值数量这两个参数的选取对预报误差的影响.从Madrigal 数据库中任意选取了5 个网格点的观测数据开展了预报试验，对不同参数设置方案的预报误差进行了对比分析.2020 年2 月8 日网格点4 (30°S，25°E)的个例分析结果表明，“3+9”方案的预报误差相对最小，天数增加或减少(例如“2+6”、“4+12”和“5+12”等方案) 都会使误差变大.进一步地，我们对5 个观测站分别进行了30 天的1～24 h 短期预报试验，综合分析了3 600 个预测点的RMSE 和NRMSE，结果显示：相比于传统的“4+12”方案，“3+9”方案在5 个观测站中均取得了更优的预报性能.具体地，所有站RMSE 平均值从0.825 TECU 降低至0.805 TECU，降低了0.02 TECU，NRMSE 平均值从11.756%降低至11.452%，降低了约0.3%.

因此，我们推测，TEC 时间序列的当前状态可能主要与前3 天的状态有关.当参与加权的观测天数增加(大于3 天)时，内在关联性小的观测值参与加权运算，可能会出现较大的状态差异，从而造成误差增大.当参与加权的观测天数减少时，可能会丢失主要的内在关联信息，从而也引起误差增大.但需要指出的是，本文提出的参数优化方案只是对传统参数方案的一个微小的改进，还无法明显改善电离层预报性能，但可作为工程实现的参考方案.

电离层随时间的变化非常复杂，除了熟知的周日变化、季节变化和太阳活动性11 年周期变化外，还存在很多小尺度的时间变化，目前我们对这些小尺度时间变化规律和控制因素的认识还不足.若要显著提高电离层短期预报性能，必须深入研究电离层参量随时间短期变化的规律和内在控制机理，这将是我们下一步研究工作的重点.