基于GNSS/UWB 的室内外连续定位方法

周振南，邹进贵，赵胤植，胡洪，蔡礼贤，周涛

(1.武汉大学 测绘学院,武汉 430079；2.武汉大学 地球空间环境与大地测量教育部重点实验室,武汉 430079；3.安徽大学 资源与环境工程学院,合肥 230601；4.广州市城市规划勘测设计研究院,广州 510060)

0 引言

随着5G 以及物联网的快速发展，基于位置服务(LBS)在人们的日常生活中变得越来越重要，室内定位逐渐成为位置服务的热点研究课题[1-2].我国科技部在“十三五”重点研发计划中部署了室内定位的攻关课题[3]，在“十四五”规划中，物联网高精度定位亦是产业数字化转型章节中技术创新的推进重点[4].加快推进室内外定位技术的研发是实施国家战略，建设社会主义现代化强国的迫切需要.

在室外环境中，全球卫星导航系统(GNSS)已经发展的非常成熟与完善，能够获得可靠的高精度定位结果，但是信号遮挡一直以来都是GNSS 一个难以解决的问题[5].在室内外的过渡区域等环境中，由于高层建筑物的遮挡和折射等因素，导致GNSS 可见卫星数目急剧下降，卫星信号质量降低，几何精度衰减因子(GDOP)变大，甚至无法单独完成定位，由此便衍生出多系统、多传感器的联合定位方式来获取更为完备与可靠的定位结果[6].脉冲无线电超宽带(IR-UWB)具有大带宽、窄脉冲和高时间分辨率等优势[7-9]，在测距、定位、无线通信等领域有着良好的抗多径和穿透能力[10]，因此超宽带(UWB)在室内定位领域有着非常广阔的发展前景.

在此之前，一些学者提出了GPS/UWB 紧组合定位模式，该模式可以增加观测的冗余度，提高定位的可靠性[11].CHIU 等[12-14]提出在复杂的城市环境下进行GPS/UWB 紧组合定位以及研究了差分GPS (DGPS)和UWB 的紧组合模型，但其在运动状态下只能达到米级的定位精度.MACGOUGAN 等[15-17]研究了用于精密定位的GPS/UWB 紧组合模型，结果表明，浮点解可以达到亚米级精度，同时也缩短了固定解的收敛时间，之后又在真实的遮蔽环境中进行紧组合定位，获得了亚米级的定位结果.尽管一些学者已经对GNSS/UWB 紧组合进行了较为深入的研究，但是大部分均是利用检核点来分析结果，对卫星拒止环境下的连续动态定位缺乏研究.考虑到松组合相比于紧组合算法简洁、易于集成、稳定性高，并且对系统的实时性和同步性要求较低，因此，本文对北斗卫星导航系统(BDS)+GPS/UWB 松组合定位方法展开研究，设计了室内外动态定位实验与过渡区域静态定位实验.利用扩展卡尔曼滤波器 (EKF) 对BDS+GPS和UWB 的定位误差状态进行最优估计，并对静态实验与动态轨迹的结果进行分析评价，以期能够充分利用UWB 的高精度测距能力来改善GNSS-实时动态定位(RTK)在室内外过渡区域的定位精度，扩展亚米级精度GNSS-RTK的作用范围，提高系统从室外到室内定位的连续性与定位结果的可用性.

1 GNSS/UWB 松组合定位模型

1.1 GNSS 相对定位

实时动态(RTK)定位属于相对定位中的一种定位方式，在较好的信号条件且载波相位模糊度固定的情况下能够达到厘米级的定位精度[14].如果模糊度未能正确固定，则得到分米级的浮点解[18].RTK 双差观测模型为

1.2 UWB 定位原理

UWB 室内定位可以基于多种原理实现，比如到达时间(TOA)、到达角度测距(AOA)、到达时间差(TDOA)、飞行时间(TOF)等，其中TOA 和TDOA 均需要发射器和接收器时间同步[19-20].文中所使用的UWB 设备采用双向测距，属于一种异步测距的方法，其中发射器使用其自身的时钟和频率来测量双向距离，不需要严格的时间同步[20-21]，如图1 所示.

图1 双向测距示意图

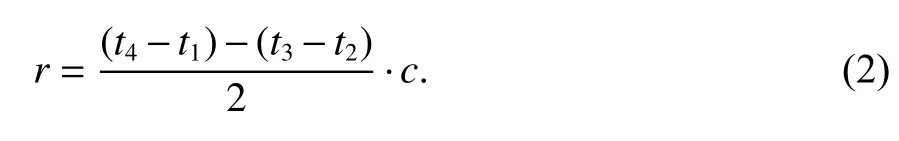
式中：c为空气中的光速；r为标签与锚节点之间的距离.

然而，时间测量是基于频率标准的，这些标准通常有偏差或者频率偏移，这种偏差通常以10-6表示[22].对于UWB 测距，在短距离内，这种偏差在短测量间隔内非常稳定，在较长的时间间隔内，由于老化、温度变化和机械应力等原因，可能会发生频率漂移[22].这可能会导致在测距期间缓慢的测距偏差，为此，在后期解算过程中需要考虑频偏的影响.

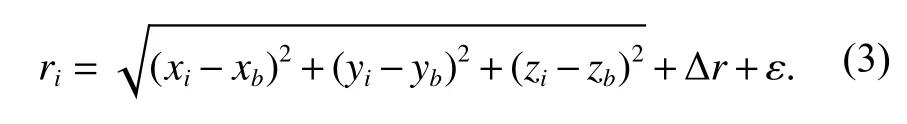
式中：(xi,yi,zi) 为标签位置；(xb,yb,zb) 为锚节点位置；Δr为测距偏差；ε 为噪声.

1.3 GNSS/UWB 松组合定位模型

位置或者速度改正数是待估参数，将GNSS 的位置解和相关方差协方差矩阵与另一个系统获得的位置解和方差协方差矩阵作为测量值输入，这种方法称为松组合[23]，如图2 所示.

图2 松组合示意图[23]

本文所使用的导航状态估计算法是基于EKF 的松组合，包括状态预测和量测更新两个过程，将移动站的位置改正数作为估计状态，BDS+GPS 相对定位获得的位置与UWB 解算得到的位置之差作为量测信息，并用估计的位置改正数对BDS+GPS 相对定位的结果进行反馈校正，数据处理结构如图3 所示.

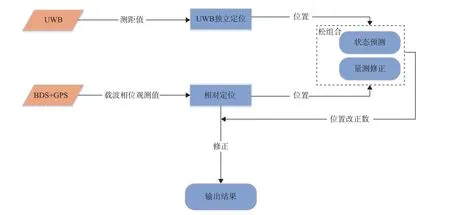
图3 数据处理结构示意图

状态方程

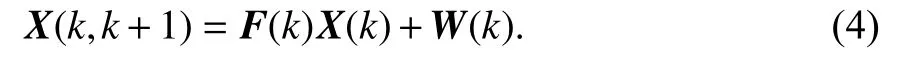
式中：X(k)=[Δx,Δy,Δz]T为位置改正数；F(k) 为状态转移矩阵；W(k) 为系统状态噪声.

量测方程

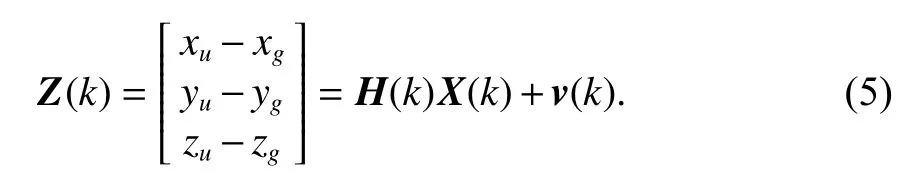
式中：(xg,yg,zg) 为BDS+GPS 相对定位结果；(xu,yu,zu)为UWB 独立定位结果；H(k) 为量测方程系数阵；v(k)为系统观测噪声.

在EKF 算法中，采用泰勒级数展开对非线性函数进行线性化，实现了原始状态方程和量测方程的近似表示[24]，之后再通过递归公式不断地预测、更新直至最后一个历元结束.

2 实验方案与程序

2.1 时间同步

在对GNSS 与UWB 进行松组合之前，两个系统需保持同一时间基准.对于GNSS 接收机来说，观测数据的时间即为GPS 时(GPST).为此，只需保证UWB 的时间系统也为GPST，而UWB 无线电将数据记录到笔记本电脑中，因此数据的时间与笔记本电脑的时间相匹配，即为协调世界时(UTC)时间，则只需后期数据处理之前将UTC 转换成GPST 即可.

2.2 GNSS-UWB 同轴安装

为了便于GNSS 与UWB 的组合解算，本次实验制作了一个天线支架，该支架能够将GNSS 接收机的天线相位中心与UWB 的天线相位中心放置于同一铅垂线上.支架的大部分材料均是金属，经过实验验证该支架对于GNSS 与UWB 的信号影响微乎其微，对于本实验可以忽略不计.同时支架上还装有一个360°棱镜，可利用全站仪记录移动轨迹作为外部参考值，GNSS-UWB 支架如图4～5 所示.

图4 静态测量设备

图5 动态测量设备

2.3 坐标基准统一

本次实验场地中控制点，已知其高精度WGS-84坐标，以此利用全站仪获取UWB 锚节点的WGS-84坐标，将双系统纳入统一的测量坐标系中实现坐标基准的统一.

3 实验与结果分析

为了验证UWB 的高精度测距能力及其对BDS+GPS 定位结果的改善情况，本研究于2022 年1 月13 日进行了两项实验，一项为室内外动态定位实验，一项为过渡区域静态定位实验.实验场地位于武汉大学诗琳通地球空间信息科学国际研究中心一楼室内外部分.实验主要设备包括1 台带有GPS1000 测量型天线的DT100 型GNSS 接收机采集GPS 与BDS的观测数据进行相对定位，8 台Time Domain 公司PulsON 系列的UWB 设备，1 台作为标签，7 台作为锚节点.GNSS 使用九峰IGS 站作为基准站进行相对定位.由于GNSS 卫星与UWB 锚节点的分布特性，高程方向精度不稳定，并且室内定位更多的是关注平面，所以在此只对平面上的定位结果进行分析评价.

在实验场地的室内外过渡区域中，由于建筑物的遮挡，GNSS 接收机观测卫星的视角受到很大程度的影响，其相比于室外开阔环境中可见卫星数较少，甚至卫星数小于4 颗而无法单独完成定位，并且环境较为复杂，影响因素较多，多路径效应更为明显，卫星信号质量降低，对定位结果会产生很大程度的影响；相比于室内封闭环境能接收到少量的GNSS 卫星信号和室内定位源的信号，但各单一定位源均无法获得连续可靠的定位结果.因此，在室内外的过渡区域需要采用多传感器的组合定位模式，充分利用所接收的不同信号源的数据，获取一个较为连续可靠的定位结果.

3.1 静态定位实验

图6 中将7 台UWB 设备根据现场情况合理地布设于场地之中，将安装好测量设备的天线支架放置于室内外过渡区域一个固定点位进行静态测量实验，观测时长约为10 min，卫星截止高度角设置为15°，GNSS 和UWB 的采样率均为1 s，以全站仪的测量结果作为外部参考值.

图6 UWB 组网示意图

对静态实验所得结果进行误差统计，利用外部参考值计算其外符合精度均方根误差(RMSE)结果如表1 所示.

表1 静态实验定位误差统计 m

由表1 可知，在室内外过渡区域，UWB 的定位精度最高，BDS+GPS/UWB 松组合与UWB 的精度相仿，BDS+GPS 在室内外的过渡区域等复杂环境下，多路径效应较为明显，反射信号较多，信噪比偏低，再加上建筑物遮挡使得卫星信号质量下降，导致先验残差偏大，增大了模糊度搜索空间，使其很难正确固定，精度最不理想只能达到米级.分析发现，BDS+GPS/UWB 松组合的定位误差介于BDS+GPS 与UWB之间，这也正是松组合定位的一个特性，定位结果的精度总是介于两单一定位源之间.BDS+GPS/UWB松组合相比于BDS+GPS 的定位精度在北(N)方向提升17.12%，东(E)方向提升77.75%，点位平面提升61.13%，可以在点位平面精度要求为亚米级的前提下，扩展GNSS-RTK 的作用范围，使其在室内外的过渡区域也能够获得较好的定位结果.由表1 可知，UWB 在N 方向的定位误差要明显高于E 方向上的定位误差，分析发现UWB 锚节点在E 方向上大致呈两侧均匀分布，但在N 方向只分布在一侧，几何构型较差，导致结果精度偏低.

3.2 动态定位实验

将上述测量支架组装成的测量设备放置在对中杆上，实验人员按照既定的路线缓慢移动测量设备，路线包括室外、室内外过渡区域和室内三部分，在移动过程中使用MS50 测量机器人记录移动站的轨迹作为外部参考值，移动站的参考轨迹如图7 所示.

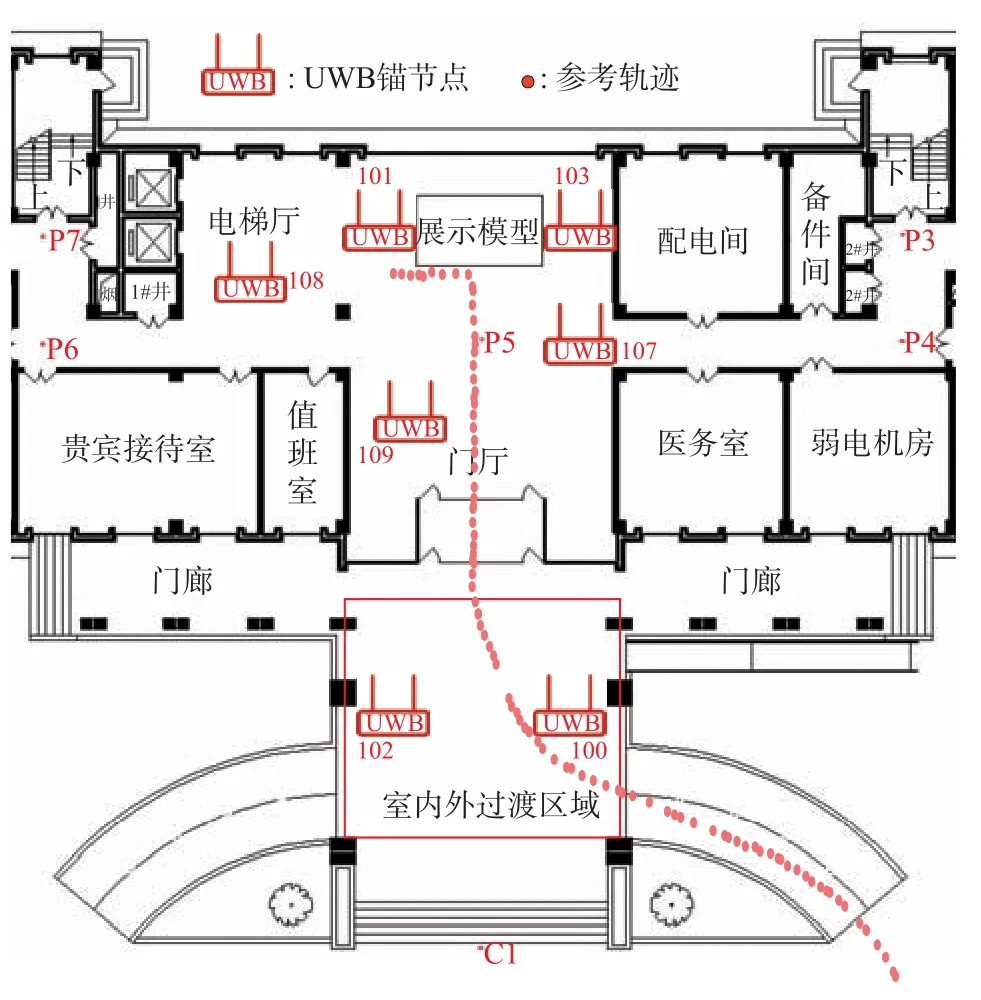
图7 真实轨迹

由于实验场地的限制参考轨迹只记录了从接近室内外过渡区域开始直至室内，室外开阔区域没有记录参考轨迹.在实验过程中，两定位源的观测值个数随着时间的变化如图8 所示，横坐标表示GPS 周内秒，纵坐标表示BDS+GPS 或者UWB 的观测值个数.

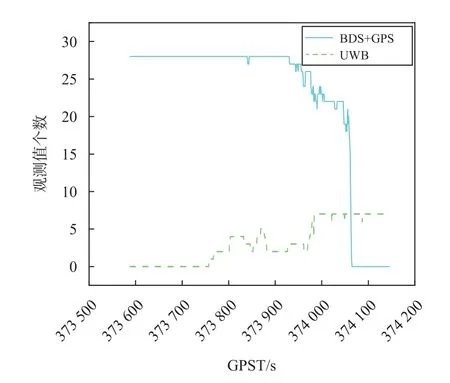
图8 两定位源观测值个数

由图8 可得，实验初始处于室外开阔区域，BDS+GPS 的可见卫星数较多而UWB 的观测值个数为0，随着移动站逐渐向室内移动，UWB 开始出现观测值，BDS+GPS 的可见卫星数逐渐减少，直至完全进入室内，BDS+GPS 的可见卫星数为0，UWB 的观测值个数最大达到7 个.当BDS+GPS 的可见卫星数减少时，UWB 系统观测值的增加恰好可以弥补这一缺陷，这也进一步地说明了进行多传感器组合定位的可行性.对动态实验的结果进行三种定位模式的解算，结果如图9～11 所示.

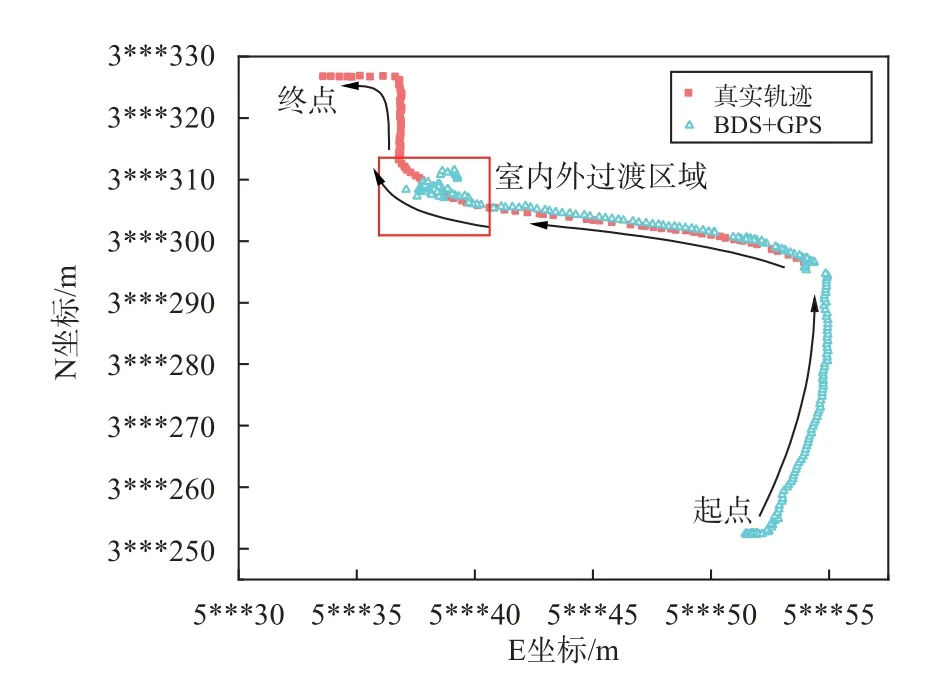
图9 BDS+GPS 定位轨迹

BDS+GPS 在室内外过渡区域复杂环境下，多路径效应较为明显，反射信号较多，信噪比偏低，再加上建筑物遮挡使得卫星信号质量下降，导致先验残差偏大，增大了模糊度搜索空间，使其很难正确固定，结果精度偏低，而UWB 凭借着其较高的测距精度，由BDS+GPS-RTK 赋予其一个较为可靠的初值，使其快速收敛，在室内外过渡区域也能够获得一个较好的结果.然而，无论是BDS+GPS 还是UWB 各单一定位源均无法获得从室外到室内连续、可靠的定位结果.从图11 可以很明显地看出，BDS+GPS/UWB松组合相比于各单一定位源在一定程度上提高了系统从室外到室内定位的连续性与定位结果的可用性.接下来对定位结果的可用性进行量化分析，由于两定位源的采样率均为1 s，在此给出各定位模式下定位结果的可用率指标，即所得定位结果的历元数占总历元数的百分比，结果如图12 所示.

图10 UWB 定位轨迹

图11 BDS+GPS/UWB 松组合定位轨迹

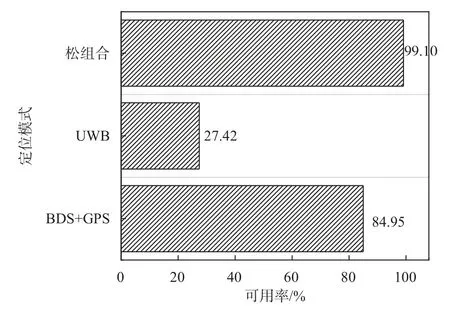
图12 定位结果可用率

由图12 可知，BDS+GPS 系统的可用率为84.95%，单UWB 系统的可用率为27.42%，松组合的可用率为99.10%，松组合相比于各单一定位源定位结果的可用率均有了一定程度的提高.

4 总结

文中针对BDS+GPS/UWB 松组合定位展开研究，设计了室内外动态定位实验与过渡区域静态定位实验，并利用EKF 对位置误差进行最优估计.实验结果表明：在室内外的过渡区域，BDS+GPS/UWB 松组合在一定程度上改善了GNSS-RTK 的定位精度，在点位平面精度为亚米级的前提下扩展了GNSS-RTK的作用范围；BDS+GPS/UWB 松组合相比于各单一定位源在一定程度上提高了系统从室外到室内定位的连续性与定位结果的可用性.