伪距单点定位两域联合平差解的等价性分析

胡小华，刘长建，张熙

(1.中国人民解放军战略支援部队信息工程大学 地理空间信息学院,郑州 450001；2.61363 部队,西安 710000)

0 引言

测绘领域中，融合多类观测数据进行联合平差的应用十分丰富，如基于观测信息以及各类导出信息的融合[1-4]、多源异构数据的融合[5-7]等，其函数模型大多为非线性模型.导航领域中，融合多系统全球卫星导航系统(GNSS)定位也越来越普遍，同样是非线性观测模型联合平差问题.

对于线性观测模型的联合平差问题中，不同等级水准网的联合平差，利用参数加权平差，理论上完全可以证明其结果与平差值域联合平差结果相同；不同等级水准网单独平差结果的联合平差，但非线性观测模型下情况却有所不同.国内外学者虽就非线性模型的线性化程度度量方法[8-9]、非线性模型的参数估计[10-14]以及非线性模型的直接解法[15-18]等进行了研究，但目前最常用的仍是将模型线性化迭代求解，即采用高斯-牛顿迭代法或迭代最小二乘法[19].由于迭代求解时，观测值联合平差时的近似值与不同类观测值单独平差的近似值不同，该不同所引起的线性化模型误差对两域联合平差结果的等价性影响如何正是本文探讨的内容.

伪距单点定位(SPP) 是20 世纪80～90 年代，最初由GPS 设计时采用的主要导航定位方法，也是目前各GNSS 处理软件提供的基本方法之一.日本东京海洋大学于2020 年12 月推出RTKLIB(b34) 版本，其SPP 模式立足于单历元迭代最小二乘求解，实现GPS、GLONASS、星基增强系统(SBAS)、准天顶卫星系统(QZSS)、Galileo、北斗卫星导航系统(BDS)、印度区域导航卫星系统(IRNSS)七个系统单频伪距任意组合时的解算.本文将以RTKLIB SPP 应用进行两域平差结果等价性的数值分析.

1 观测值域联合平差解

RTKLIB SPP 模式中，GNSS 伪距观测方程形式上被统一表为

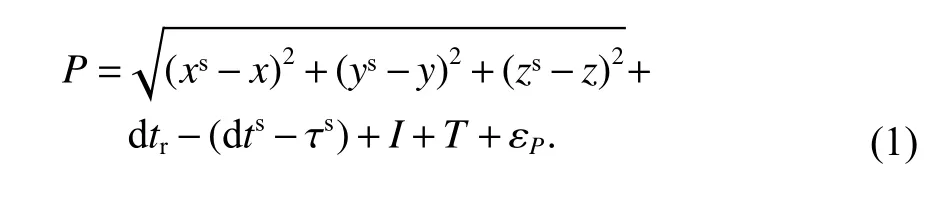
式中：P为某系统选定的单频伪距观测值；(x,y,z)、(xs,ys,zs)为 接收机 和卫星坐标；dtr、dts为接收机和卫星钟差(以距离为单位)，当为非GPS 时，dtr为接收机在该系统中的钟差与在GPS 中的钟差之差或系统间时延偏差；τs为卫星端硬件延迟或差分码偏差；I、T为电离层、对流层延迟项；εP为伪距多路径效应等未模型化误差和测量噪声之和.

该模式的未知参数固定设置为8 个且顺序保持不变，即

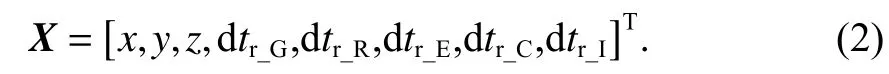
式中，G、R、E、C、I 分别代表GPS、GLONASS、Galileo、BDS、IRNSS (SBAS、QZSS 视为同GPS).借助虚拟观测值思想，RTKLIB SPP 巧妙地实现了同一套程序求解GNSS 多个系统任意组合时的参数.

为方便讨论，下面将各GNSS 的接收机钟差参数恢复为各系统的原始钟差，这两种解法是等价的[19].于是，各GNSS 伪距观测值联合平差的误差方程可表为

式中：Pi(i=G,R,E,C,I)表示i系统经过相应改正后的所有伪距向量；Vi为对应的残差；fi为对应的欧几里德几何距离向量；为对应的接收机三维坐标平差值或位置解向量；ei为对应的元素全为1 的列向量；为对应的各系统接收机原始钟差平差值.

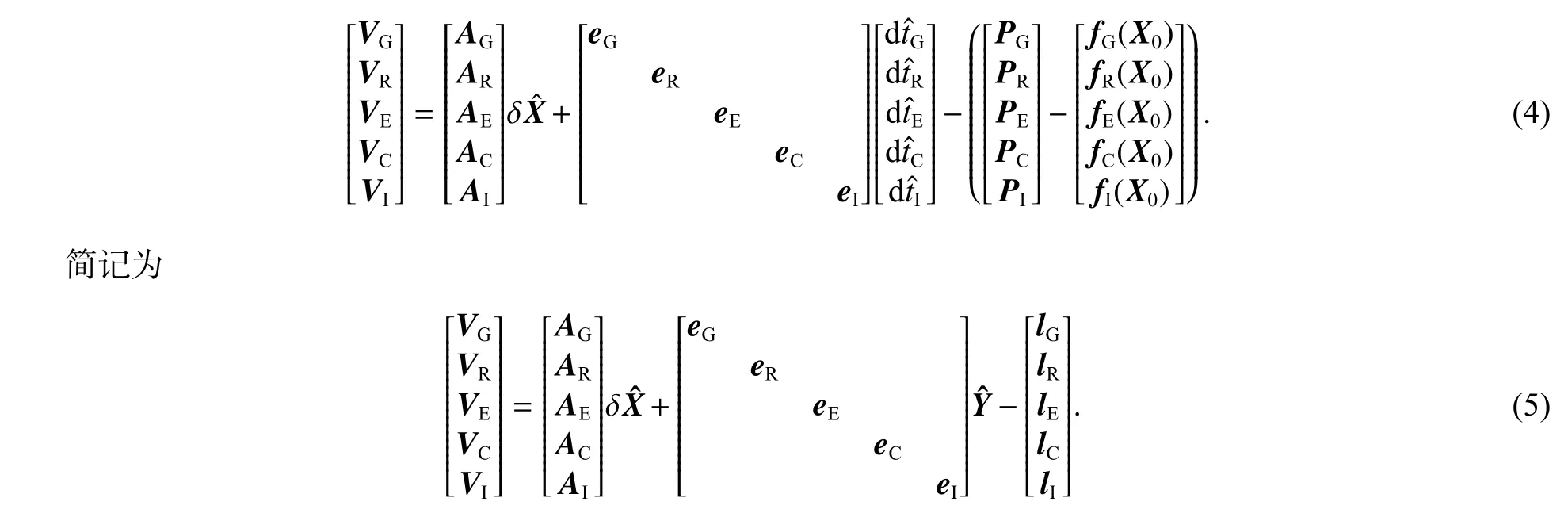
根据参数分组平差求解原理[20]，由式(7)可解得

位置解及其协方差阵为：

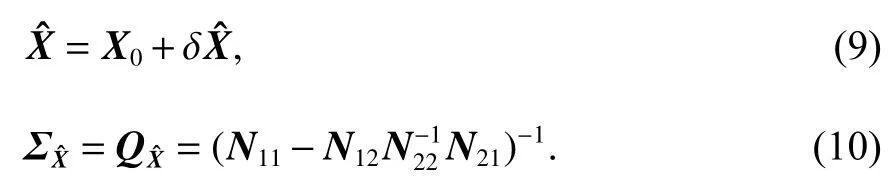
式(8)～(10)即观测值域联合平差位置解迭代公式，其中，本次迭代的X0取为上次迭代计算的，直至收敛(RTKLIB SPP 设置的条件为要指出的是，式(10)是用验前单位权方差求得的，因为用式(6)定权时由于每历元求解时多余观测数较少，使用验前单位权方差进行精度估计是RTKLIB 等软件通常采用的方法.

2 平差值域联合平差解

下面采用两种方法推导出平差值域联合平差位置解公式.

2.1 推导方法一

将式(8)变形为

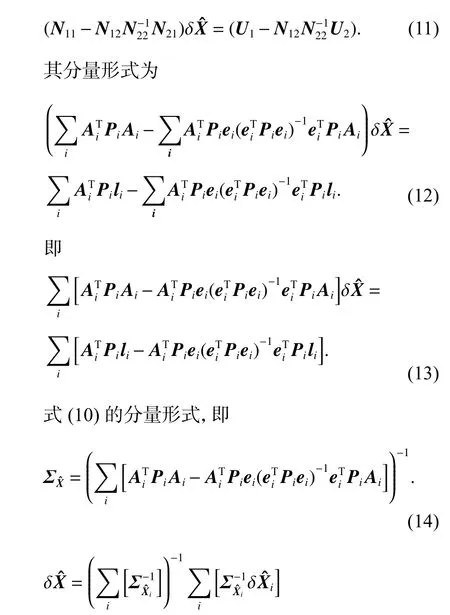
设每个GNSS 可以单独平差，相应式(5)、式(6)，平差模型为

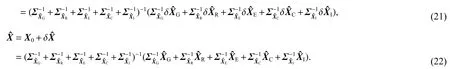
同样地，式(14)又可以写为

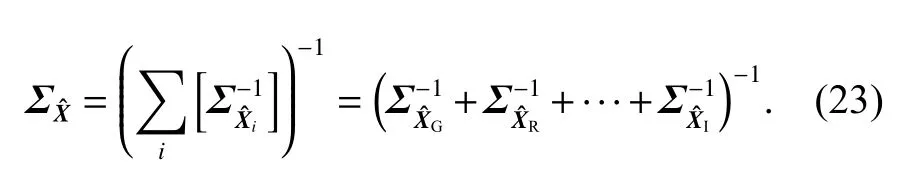
式(22)～(23) 为平差值域联合平差位置解公式，由式(8)～(10)等价变形得到，假设了单系统每次迭代求解时的X0与观测值域联合平差时相同.不难理解，这一假设实际中难以满足，由此造成的两域联合平差结果的差异和fi有关，并且不同非线性模型非线性强度不同，由线性化近似导致的误差也不同[21].此外，也不难理解，若fi为线性函数则不存在此问题，因为线性模型平差解不需要迭代且与近似值的选取无关.

2.2 推导方法二

直接视式(18)中的Xˆ˙i为历元位置X的虚拟观测值[1]，可列平差值域联合平差的模型为：

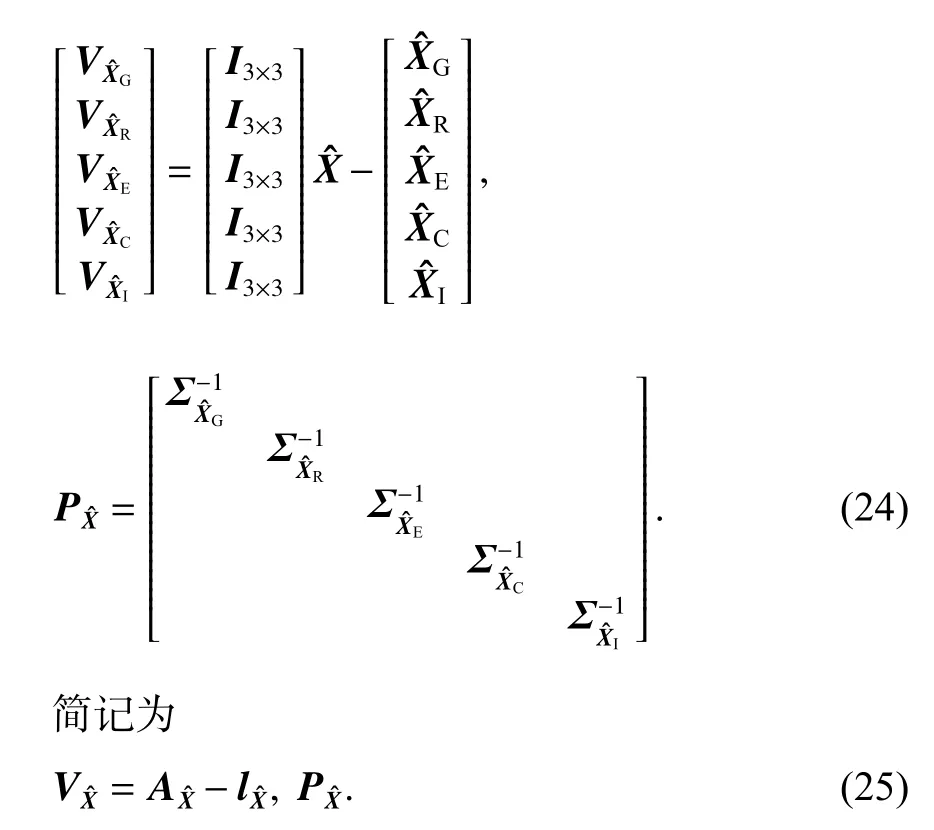
于是，根据参数平差公式得法方程为

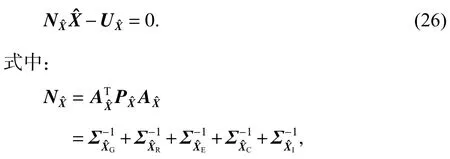
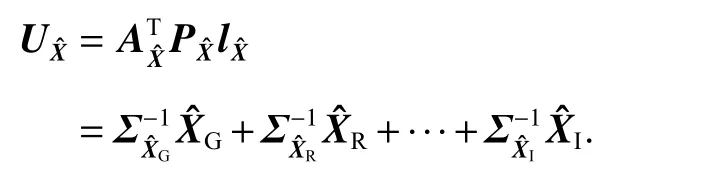
平差值域联合平差的位置解及其协方差阵为：

该两式与式(22)～(23)相同.

3 SPP 两域联合平差解等价性分析

由前知，对于非线性观测模型，欲使两域平差解完全相同，需要每次迭代时观测域联合平差的近似值与不同类观测值单独平差的近似值X0相同，但实际中难以保证.这一不同造成两域联合平差解差异有多大，与具体应用的非线性函数有关.下面以LHAZ 站2021-02-18 T 00:10:30 的RTKLIB SPP 结果为例进行分析，该历元GPS、BDS、GLONASS、Galileo 均能单独取得收敛解.

算例一为该历元GPS、BDS 进行两域联合平差，结果如表1 所示.表中，x、y、z表示位置解的平差值、表示表示sign(·)表示该项的符号.由表1 可知，两系统两域平差解在毫米量级上相同.

算例二为该历元GPS、BDS、GLONASS 进行两域联合平差，结果如表2 所示.表中符号同算例一.由表2 同样可知，三系统两域平差在毫米量级上也相同.

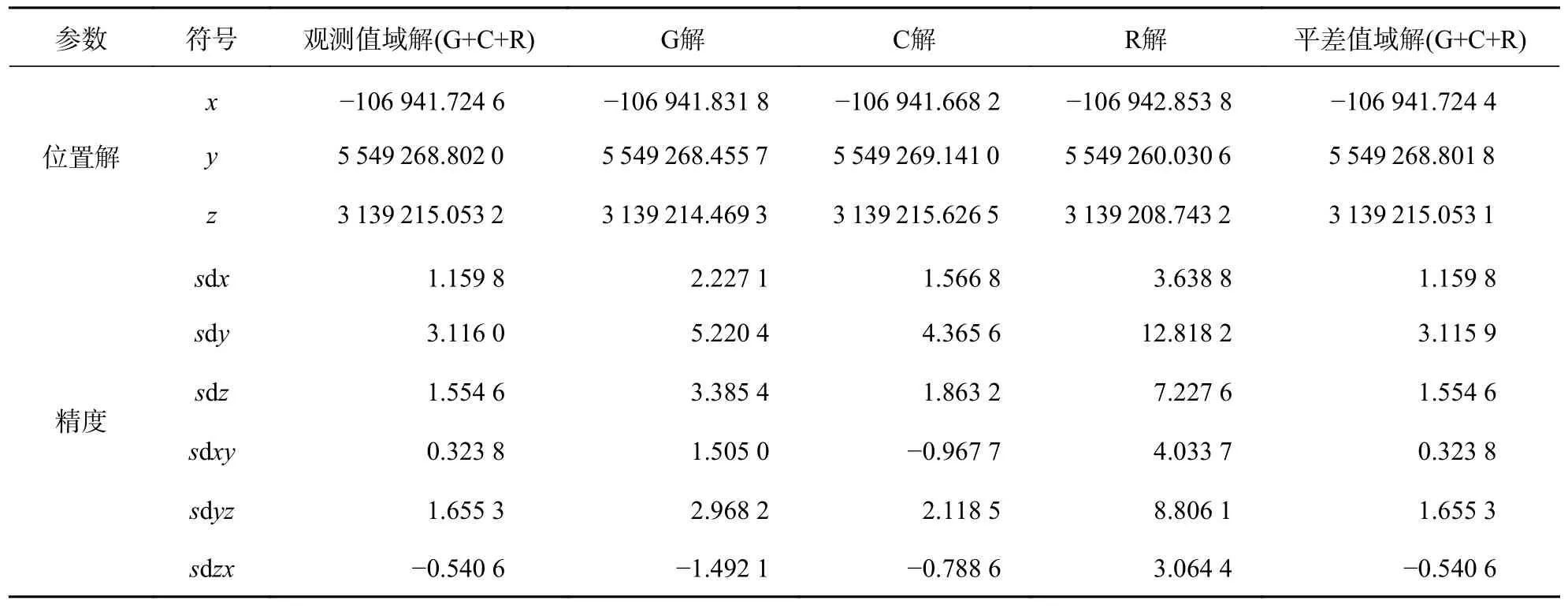
表2 GPS、BDS、GLONASS 两域平差结果 m

算例三为该历元GPS、BDS、GLONASS、Galileo进行两域联合平差，结果如表3 所示.表中符号同算例一、算例二.表3 同样表明了四系统两域平差在毫米量级上也相同.

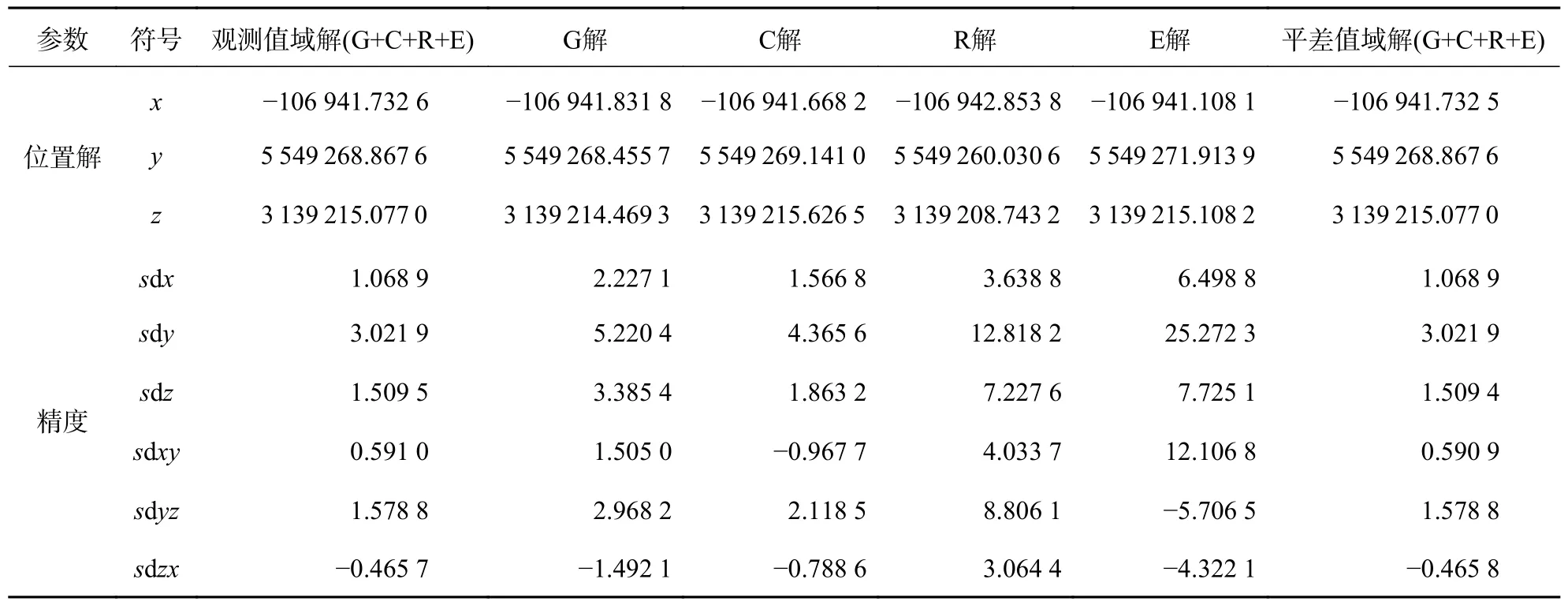
表3 GPS、BDS、GLONASS、Galileo 两域平差结果 m

综合以上3 个数值算例可见，在组合系统和单系统求解配置相同情况下(如高度限制角相同等)，RTKLIB SPP 观测值域联合平差解和平差值域联合平差解在毫米量级上完全相同，受非线性函数模型线性化的影响很小，其原因可以解释为观测值域单系统和联合平差的收敛解相差很小，它们收敛解的前一次解也相差较小，由此引起的线性化误差差异可以忽略不计.另外还要说明的是，上述三个算例中单BDS 和含有BDS 组合系统的观测值域联合平差时，RTKLIB SPP 均检测到BDS C02 卫星异常，以上收敛解均为排除该星后的收敛解，这进一步表明了异常情况下两域平差结果在毫米量级上也是等价的.

4 结论

当采用迭代最小二乘求解时，本文就SPP 模型探讨了非线性误差方程两域联合平差解的等价性，主要结论如下：

1)非线性观测模型，计算中无需进行线性化和迭代计算，非线性模型各类观测值单独迭代求解时的近似值与观测值域联合平差迭代求解时的近似值不同，其对两域联合平差解的影响与非线性函数的非线性强度相关，需具体问题具体分析；

2)在配置相同的情况下，对2021 年2 月18 日LHAZ 站单历元数据采用RTKLIB SPP 的计算结果表明，不同系统组合的两域平差位置解在毫米量级上数值相同，对于SPP 应用可以认为两域联合平差解等价；

3)本文探讨的内容具有一定的普遍性，如关于多系统GNSS 的其他应用等，它们两域联合平差解的等价性可类似进行探讨，其中，如何构造优秀的算法，尽量缩小两域平差解的差异，仍是一个重要研究课题.