iGMAS分析中心产品一致性分析及其应用研究

苗 伟，王潜心，胡 超，王泽杰

(1. 中国矿业大学自然资源部国土环境与灾害监测重点实验室，徐州 221116;2.中国矿业大学环境与测绘学院，徐州 221116)

0 引言

随着全球导航卫星系统(Global Navigation Satellite System，GNSS)不断壮大, 高精度 GNSS 已广泛应用于地球科学研究和社会生产活动。立足于我国北斗卫星导航系统(BeiDou Navigation Satellite System，BDS), 中国从2012 年正式启动国际GNSS监测评估系统(International GNSS Monito-ring & Assessment System, iGMAS)建设。该系统的主要任务是建立BDS/GPS/GLONASS/Galileo导航卫星全弧段、多重覆盖的全球近实时跟踪网，以及具备数据采集、存储、分析、管理和发布等功能的信息服务平台，对GNSS的运行状况和主要性能指标进行监测和评估，生成高精度精密星历、卫星钟差、地球定向参数、跟踪站坐标和速率、全球电离层延迟模型和GNSS完好性等事后产品，支持卫星导航技术试验和监测评估，服务于科学研究和各类应用[1]。

目前，iGMAS已建成13家分析中心，各分析中心功能相同，可独立开展工作，且均可为iGMAS提供各类 GNSS产品。文献[2]指出，各分析中心提供的最终轨道和钟差产品相对于MGEX轨道和钟差产品的精度，如表1所示。

表1 iGMAS分析中心最终轨道和钟差产品相对于MGEX最终轨道和钟差产品的精度

由表1分析可得，各分析中心BDS的轨道和钟差产品精度略低于GPS/GLONASS/Galileo轨道和钟差产品的精度。近年来，国内学者一直致力于研究提高BDS轨道和钟差精度的方法。Qianxin Wang指出，利用BDS-2/BDS-3综合精密时钟偏移量进行超快速定轨的方法，可以使BDS-2/BDS-3观测轨道的精度分别提高9.2%和5.0%，预测轨道的精度可提高到82.2%[3]；Chao Hu和Qianxin Wang等提出的基于BDS-2和BDS-3联合估计的BDS卫星超快速时钟偏移预测改进模型，在预测时间为18h内时，BDS-2的时钟偏移量预测精度提高了30.7%～47.3%，BDS-3的时钟偏移量提高了49.9%～59.3%[4]；Qianxin Wang和Chao Hu等提出的基于精度因子的全球导航卫星观测系统超快速轨道修正方法，对于在观测轨道的最后3h，由于观测不足而产生的观测超快速轨道误差可以修正12%～22%[5]。

国际 GNSS 服务组织(International GNSS Service，IGS)是国际大地测量协会(International Association of Geodesy，IAG)为支持大地测量和地球动力学研究于1993年组建的一个国际协作组织，共有12个分析中心为其提供轨道和钟差等产品[6]。多年来，国内外许多学者针对IGS不同分析中心轨道和钟差产品的一致性做了很多研究。Jan Kouba和Tim Spronger提出了一种事后钟差综合方法，该方法首先进行钟差与轨道、钟差与站坐标产品间的一致性改正，之后消除各个分析中心钟差间的系统偏差，实验结果表明，钟差产品与轨道产品、ERP产品、站坐标产品间的一致性达到毫米级[7]；Ouba J和 Mireault Y等使用IGS综合产品进行了精密单点定位实验，详细分析和阐述了定位过程中涉及的各项误差改正模型，定位结果表明，该综合产品可以获得cm级的定位精度[8]；Steigenberger P和Hugentobler U等通过分析4个多GNSS实验项目(Multi-GNSS Experiment，MGEX)分析中心的Galileo产品在20周内的轨道和时钟质量发现：比较各个分析中心的轨道，具有5～30cm的一致性，相邻2天轨道不连续误差为4～28cm，而其拟合均方根值在1～7cm之间[9]；魏娜分析了IGS各类产品间的一致性，并指出随着绝对天线相位中心模型的引入，IGS框架和国际地球参考框架(Interna-tional Terrestrial reference Frame，ITRF)的尺度一致性具有显著提高[10]；陈俊平通过对比IGS不同数据分析中心提供的GNSS精密时空产品发现，各分析中心的轨道和钟差存在明显差异，并且轨道和钟差的相对偏差存在很强的相关性——呈现负相关特性。类比IGS，iGMAS不同分析中心之间可能也存在产品一致性问题[11]。

本文通过对iGMAS多家产品进行分析比较发现，iGMAS不同分析中心之间确实存在产品一致性问题，不同分析中心轨道径向和钟差相对偏差呈现强相关，并且还具有一定的周期特性。基于以上发现，本文主要研究了以下几个方面：1)结合具体数据分析了iGMAS不同分析中心最终轨道和钟差的相关特性，并通过求解相关系数加以说明；2)对不同分析中心最终钟差的相对偏差进行周期特性分析，寻找主周期；3)根据上面提取的周期，对各个分析中心的最终钟差进行建模拟合，求得原始钟差与拟合值的残差，以求得的残差对不同分析中心的钟差进行定权，最后将求得的各分析中心的钟差加权平均值作为钟差综合值。结果表明，本文提出的钟差综合方法，可以提高不同分析中心钟差的一致性。

1 轨道与钟差相关性分析

iGMAS目前已建成13家数据分析中心，每个分析中心都在为其提供轨道和钟差等产品。为分析不同分析中心轨道和钟差的相关性，本文选取iGMAS 5家数据分析中心——中国科学院测量与地球物理研究所(Institute of Geodesy and Geophysics，Chinese Academy of Sciences，IGG)、中国人民解放军信息工程大学(Information Enginee-ring University，LSN)、中国科学院国家授时中心(National Time Service Center， Chinese Academy Of Sciences，NTS)、中国科学院上海天文台(Shang-hai Astronomical Observatory，SHAO)以及武汉大学(Wuhan University，WHU)提供的2019年9月18日～20日这3天的最终轨道和钟差产品作为轨道与钟差相关性分析的数据。

基于以上选取的数据，分别对比IGG&WHU、LSN&WHU、NTS&WHU、SHA&WHU的轨道与钟差。以IGG&WHU为例具体介绍了对比方案：首先将2家分析中心相同历元的轨道径向和钟差分别作差，得到轨道径向和钟差直接差值，为了消除不同分析中心之间因参考基准不同带来的系统偏差，每个导航系统各选取1颗卫星作为参考卫星，接着将第一步求得的直接差值与参考星的直接差值相减，得到2家分析中心每颗卫星轨道径向和钟差的相对偏差；以相同的方法求得LSN&WHU、NTS&WHU、SHA&WHU 的每颗卫星轨道径向和钟差的相对偏差。比较分析发现，不同分析中心提供的最终轨道以及钟差在去掉系统性偏差后仍然存在明显的不一致。每家分析中心每个卫星系统选取了1颗卫星作为示例，其他卫星类似。对比结果如图1～图4所示。

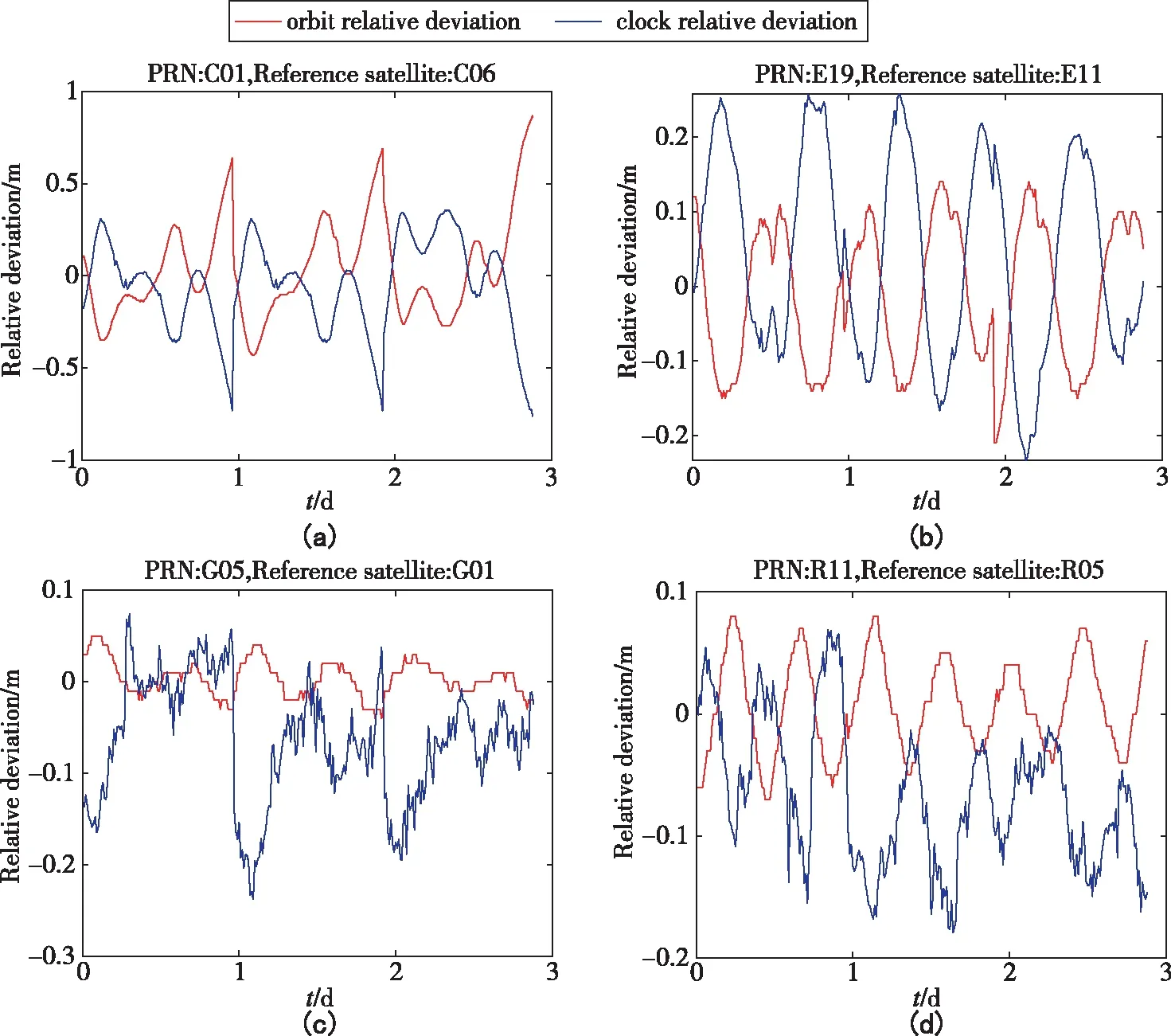
图1 IGG/WHU 卫星轨道径向以及钟差的相对偏差Fig.1 Relative deviations of satellite orbit radial and clock offsets between IGG and WHU products

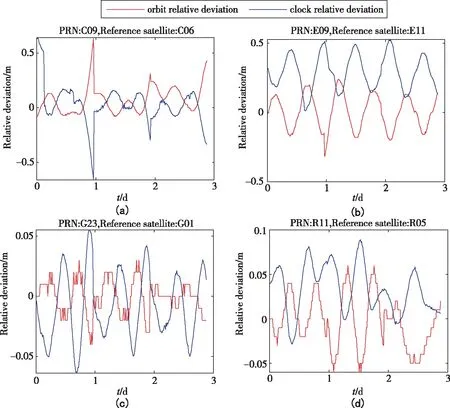
图2 LSN/WHU 卫星轨道径向以及钟差的相对偏差Fig.2 Relative deviations of satellite orbit radial and clock offsets between LSN and WHU products

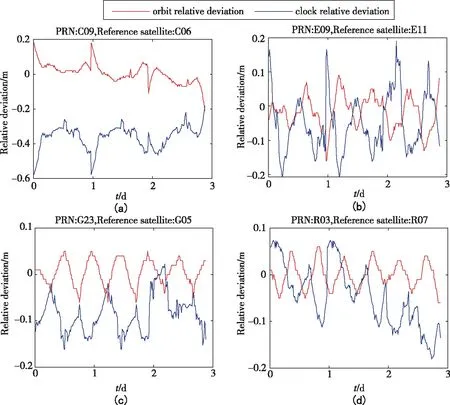
图3 NTS/WHU 卫星轨道径向以及钟差的相对偏差Fig.3 Relative deviations of satellite orbit radial and clock offsets between NTS and WHU products

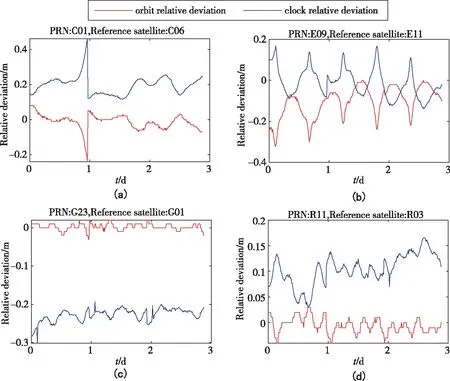
图4 SHA/WHU 卫星轨道径向以及钟差的相对偏差Fig.4 Relative deviations of satellite orbit radial and clock offsets between SHA and WHU products

从图1～图4可以发现，5家分析中心的轨道和钟差均存在周期特性，各家分析中心的BDS、Galileo、GPS、GLONASS卫星轨道径向最大偏差以及钟差最大偏差如表2所示。从表2中可以发现，除了IGG&WHU的BDS外，轨道相对偏差均小于钟差相对偏差，这可能是因为轨道径向误差被钟差吸收了所导致的。此外，从图中还可以看出，各家分析中心的轨道径向相对偏差与钟差相对偏差呈现出负相关，其中BDS和Galileo的负相关现象比较明显，GPS和GLONASS相对较弱。以IGG和WHU的轨道径向和钟差差值为例，求取二者的相关系数，以轨道径向相对偏差差值为纵坐标，钟差相对偏差差值为横坐标，相关系数如图5所示。从图5可以看出，BDS和Galileo的负相关现象比较明显，GPS和GLONASS相对较弱，仅呈现一定的相关性。根据式(1)计算可得BDS、Galileo、GPS、GLONASS卫星的轨道径向相对偏差与钟差相对偏差相关系数分别达到 -0.940、-0.931、-0.576、-0.722，与图5反应的信息一致。

(1)

式中，clk表示钟差相对偏差差值;orb表示轨道相对偏差差值。

表2 各家分析中心BDS、Galileo、GPS、GLONASS卫星轨道径向最大偏差以及钟差最大偏差

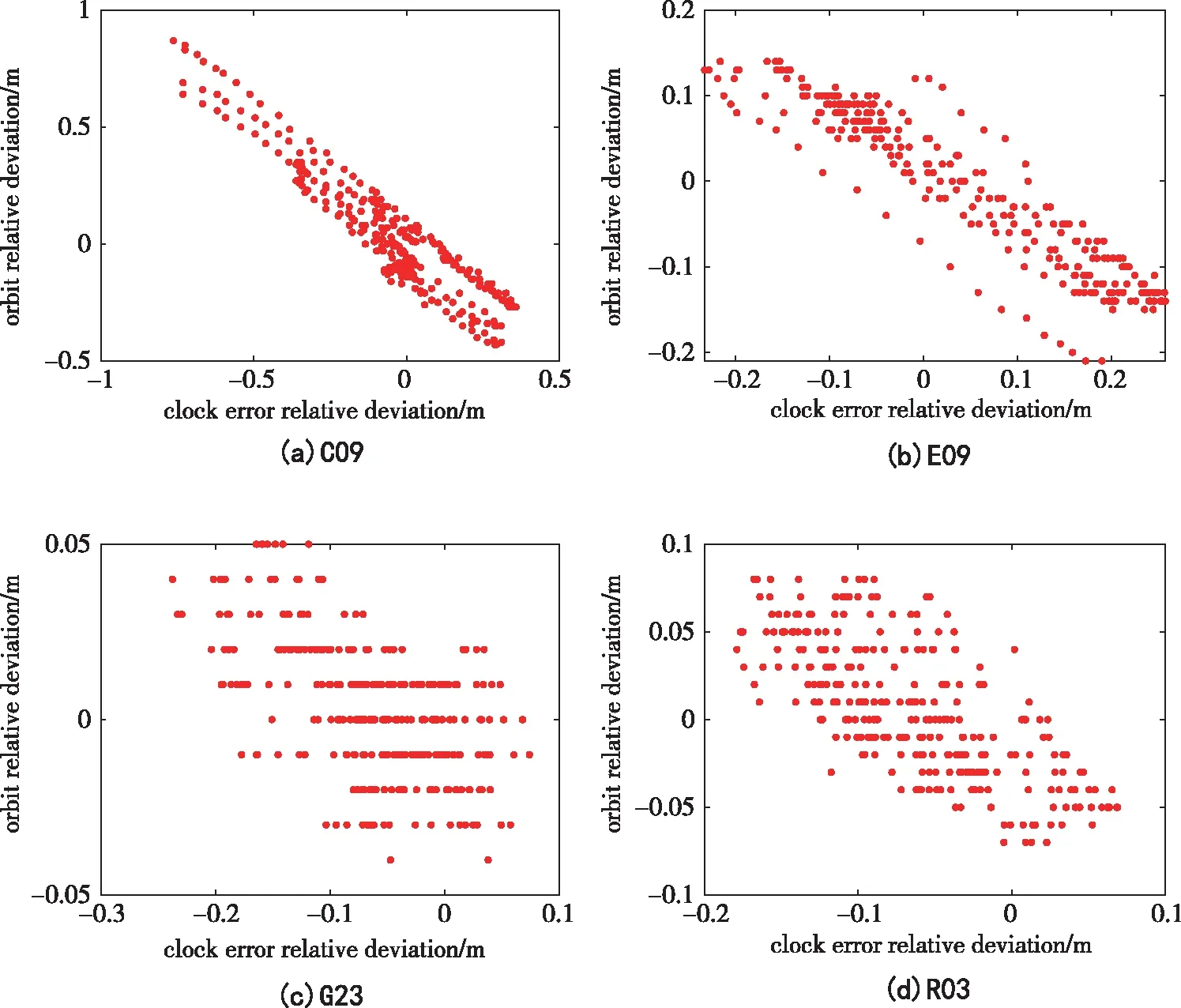
图5 IGG&WHU 卫星轨道径向以及钟差的相对偏差及其相关性Fig.5 Relative deviations of satellite orbit radial and clock offsets between SHA and WHU products and their correlations

由以上实验分析可知，各家分析中心除了轨道和钟差解算基准不同外，各家的解算模型也有所不同；但由于解算模型不同而产生的模型误差，轨道径向误差与钟差误差可以相互抵消一部分。

2 顾及相关性的钟差产品分析

卫星轨道和钟差高度相关，尤其是轨道径向误差会被卫星钟差所吸收，因此在钟差数据中会有一定的周期特性[12]，这与第1节的实验现象相符。由于实际情况下的GNSS卫星钟差的周期约为半个恒星日，采用采样长度为1天的钟差数据进行频谱分析时，数据长度相对较短，难以得到准确的频率[2]。故本节取iGMAS 5家数据分析中心(IGG、LSN、NTS、SHA、WHU)提供的2019年7月5日～8月5日这1个月的最终精密钟差数据，采用第1节相同的方法求取各家分析中心的钟差相对偏差，并利用快速傅里叶变换(Fast Fourier Transform，FFT)频谱分析方法对其进行周期特性分析[13]，基于相对偏差的主要频率，分析了不同分析中心钟差相对偏差的周期特性[14-15]。在采用 FFT 将信号从时间域转换到频率域的过程中，原始信号被拆分为多个正余弦信号。在分解出的正余弦信号中，每个信号都具有自己独特的频率，可以通过功率谱函数来体现一个信号在原始信号中的作用，信号的功率谱越大则表明该信号在原始信号中的作用越大，否则越小[2]。根据频谱分析结果中振幅的大小来选择钟差数据中的显著周期项。以SHA与WHU 这2家分析中心提供的卫星钟差的相对偏差为例，BDS、Galileo、GPS、GLONASS四系统选取的参考星分别为C06、E11、G01、R05，主频率分析结果如图6所示。

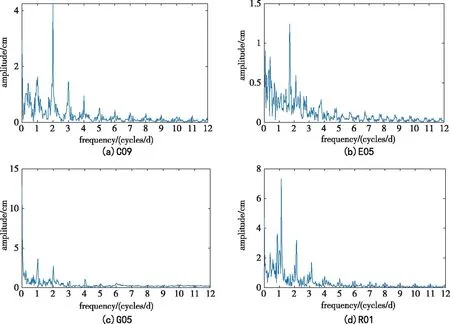
图6 SHA/WHU 卫星钟差相对偏差频谱分析Fig.6 Spectrum analysis of satellite clock offsets’s relative deviation between SHA and WHU

从图6可以看出，BDS、GPS、GLONASS有明显的12h和24h周期项，Galileo有明显的12h周期项，但24h周期项不明显；除此之外，BDS还有48h、8h和6h周期项，GLONASS还有明显的8h周期项。四系统钟差相对偏差主周期项存在差异，BDS和Galileo的主周期项均约为12h，而GPS和GLONASS的主周期项约为24h。对iGMAS其他分析中心精密钟差相对偏差的周期项分析结果与上述类似，这与第1节的实验现象相符。

基于上面钟差周期特性的分析结果，本文提出了构建多项式加周期项拟合模型对不同分析中心提供的最终精密钟差产品进行拟合，求得原始钟差值与拟合值的残差值，接着利用残差值进行定权，从而求得2家分析中心的加权均值作为钟差综合值，以此提高不同分析中心钟差产品的一致性。具体实施方案可分为以下三种。

方案一：

1)采用一次多项式加1个周期对分析中心的原始钟差产品进行拟合得到拟合值，求取原始钟差与拟合值的残差值，并利用残差值进行定权，求取2家分析中心的加权平均值作为钟差综合值；

2)采用一次多项式加2个周期对分析中心的原始钟差产品进行拟合得到拟合值，求取原始钟差与拟合值的残差值，并利用残差值进行定权，求取2家分析中心的加权平均值作为钟差综合值；

3)采用一次多项式加3个周期对分析中心的原始钟差产品进行拟合得到拟合值，求取原始钟差与拟合值的残差值，并利用残差值进行定权，求取2家分析中心的加权平均值作为钟差综合值；

4)采用一次多项式加4个周期对分析中心的原始钟差产品进行拟合得到拟合值，求取原始钟差与拟合值的残差值，并利用残差值进行定权，求取2家分析中心的加权平均值作为钟差综合值。

方案二：与方案一形式类似，将一次多项式替换为二次多项式后，分别加1～4个周期对钟差产品进行综合。

方案三：与方案一形式类似，将一次多项式替换为三次多项式后，分别加1～4个周期对钟差产品进行综合。

三种实验方案具体流程如图7所示。

基于以上提出的三种方案，本文选取了中国矿业大学(China University of Mining and Technology，CUM)、NTS、SHA以及WHU这4家分析中心提供的2019年7月21日当天的最终钟差产品进行产品综合，分别将CUM、NTS、SHA的钟差产品与WHU的钟差产品进行综合。以ISC提供的钟差产品为基准，计算各家分析中心的原始钟差值和综合钟差值相对于ISC钟差的相对偏差以及相对偏差的标准偏差(Standard Deviation，STD)值，BDS、Galileo、GPS、GLONASS这4个系统选取的参考星分别为C06、E11、G01、R05。以SHA&WHU为示例，结果如图8和表3所示，STD值越小，说明钟差综合精度越好。

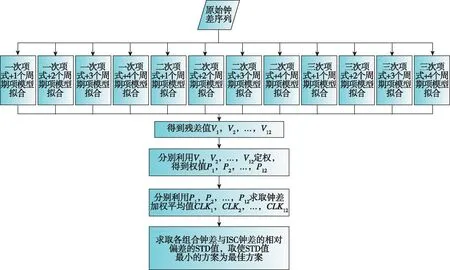
图7 实验方案流程图Fig.7 Experimental scheme flow chart

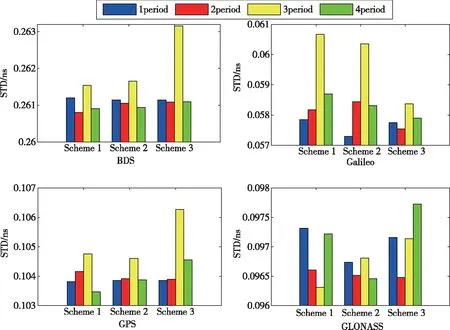
图8 SHA&WHU综合钟差STD值Fig.8 STD value of SHA &WHU combination clock offsets

表3 SHA&WHU综合钟差STD值

由图8可以明显地看出，使BDS、Galileo、GPS、GLONASS这4个系统STD值最小的方案各不相同，对于BDS，采用一次多项式+2个周期的综合模型得到的综合钟差精度最好；而对于Galileo、GPS、GLONASS，则分别采用二次多项式+1个周期、一次多项式+4个周期、一次多项式+3个周期综合模型得到的综合钟差相对偏差的STD值最小。结合图6，对4个系统卫星钟差进行谱分析发现，4个系统卫星钟差的主周期不尽相同，故引起不同系统需要不同综合模型现象的原因可能是因为BDS、Galileo、GPS、GLONASS主周期不同导致的。除了4个导航系统采用的模型不同外，CUM&WHU以及NTS&WHU采用的综合模型也不尽相同，下面将详细介绍各家分析中心采用的综合模型。

依然以SHA&WHU钟差综合为例，由以上分析可知，SHA&WHU钟差综合根据不同的卫星系统采用不同的模型，如表4所示。

表4 实验模型选择

选取2019年8月10日当天的最终钟差产品进行产品综合，以ISC提供的钟差产品为基准，计算各家分析中心的钟差和综合钟差相对于ISC钟差的相对偏差。由于原始钟差中存在跳变现象，对钟差综合带来了不好的影响，故本文通过设置阈值来剔除发生跳变的历元钟差，然后用前后历元钟差的平均值代替剔除的历元钟差。剔除函数如式(2)

difclki=

(2)

式中：difclki-1、difclki、difclki+1分别表示某一卫星在第i-1、i、i+1历元的钟差相对偏差；δ表示设置的阈值，此处设置为0.5ns。原始钟差序列经过处理后，即可进行钟差综合， 综合方法前文已经介绍，在此不再赘述。

综合结果如图9～图12所示。图9～图12中，蓝色、红色、黄色实线分别代表综合钟差与ISC钟差、SHA与ISC钟差、WHU与ISC钟差的相对偏差，BDS、Galileo、GPS、GLONASS这4个系统选取的参考星分别为C06、E01、G01、R05。由图9～图12可以看出，各系统综合钟差相对偏差值一直处于SHA和WHU中间，说明本文提出的钟差综合策略能够很好地对不同分析中心提供的钟差产品进行综合，以提高不同分析中心钟差产品的一致性。

进一步分析SHA&WHU、CUM&WHU、NTS&WHU钟差综合的相对偏差STD值，如图13所示。

由图13可以看出，各分析中心钟差综合相对偏差的STD值一直处于各自提供的钟差相对偏差STD值中间。以C11卫星为例，SHA&WHU的综合钟差、SHA和WHU的STD值分别为0.165ns、0.262ns、0.189ns；CUM&WHU的综合钟差、CUM和WHU的STD值分别为3.031ns、3.121ns、2.997ns；NTS&WHU的综合钟差、CUM和WHU的STD值分别为3.120ns、3.241ns、2.998ns。这与上文实验现象相符，说明本文提出的钟差综合策略可以提高各分析中心最终钟差产品的一致性。

图14和图15分别描述了本文提出的钟差综合方法和ISC中心钟差综合策略，由于ISC钟差综合策略前期采用逐历元校准的方法，因此会受到所选择的参考分析中心钟差质量的影响。相对于ISC钟差综合方案，本文提出的钟差综合方法首先需要找到适合2家分析中心的钟差模型，进而分别对2家分析中心的原始钟差序列进行拟合，求得残差值6，并以此进行定权，这样就会消除由于所选择的参考分析中心钟差质量不好带来的误差。

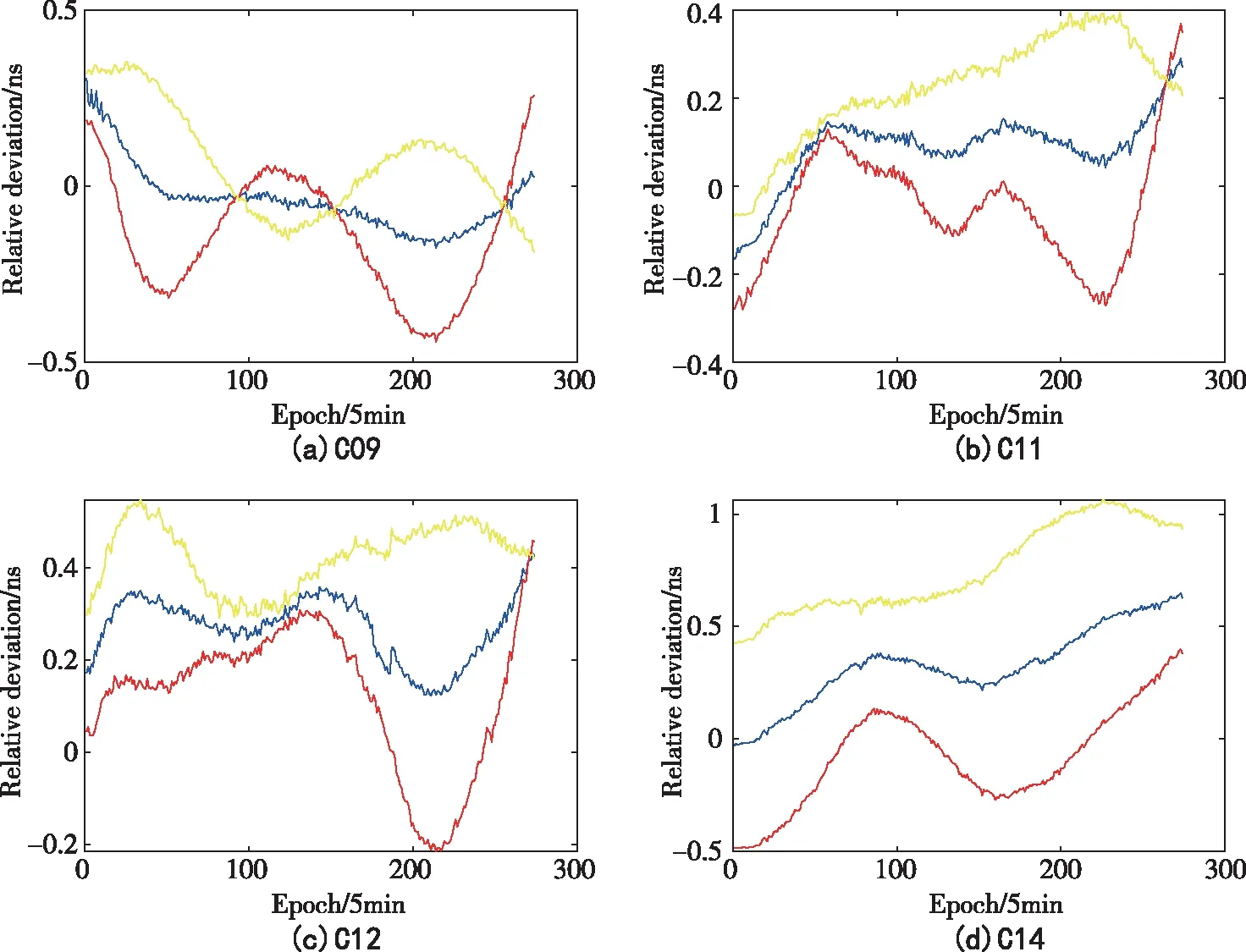
图9 SHA&WHU 北斗钟差综合相对偏差Fig.9 BDS clock offsets relative deviation of SHA&WHU

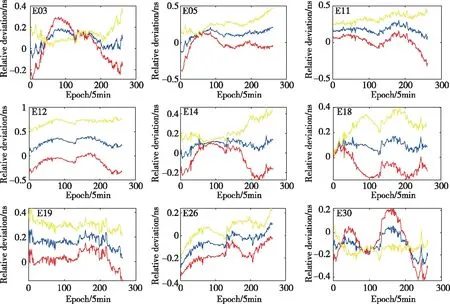
图10 SHA&WHU Galileo钟差综合相对偏差Fig.10 Galileo clock offsets relative deviation of SHA&WHU

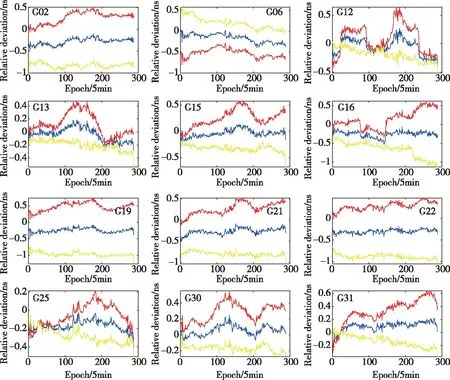
图11 SHA&WHU GPS钟差综合相对偏差Fig.11 GPS clock offsets relative deviation of SHA&WHU

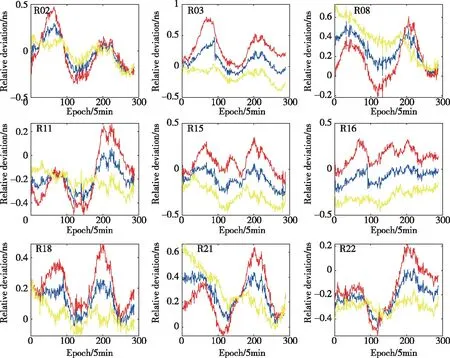
图12 SHA&WHU GLONASS钟差综合相对偏差Fig.12 GLONASS clock offsets relative deviation of SHA&WHU

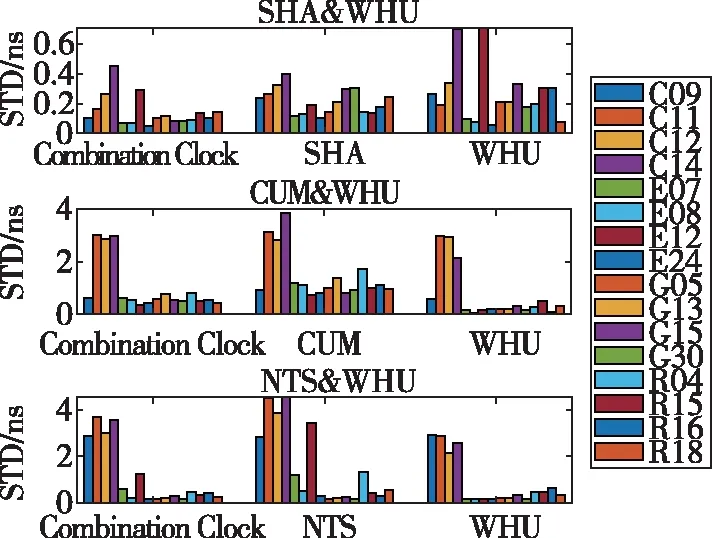
图13 SHA&WHU、CUM&WHU、NTS&WHU钟差综合的相对偏差STD值Fig.13 The relative deviation STD values of combination clock offsets of SHA&WHU, CUM&WHU and NTS&WHU

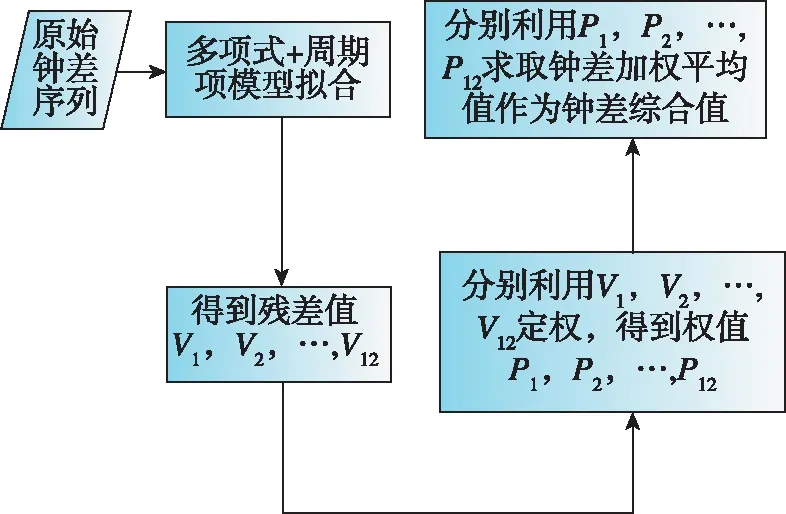
图14 本文钟差综合方法Fig.14 The synthesis method of clock offsets in this paper

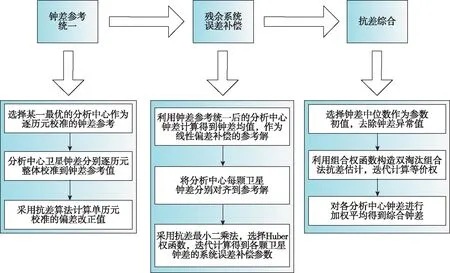
图15 ISC综合中心钟差综合策略Fig.15 Integrated strategy of clock offsets in ISC integrated center

3 结论与展望

本文针对iGMAS不同分析中心的轨道产品和钟差产品本身之间存在的一致性问题，提出了通过建立多项式+不同周期项模型对钟差产品进行拟合求得残差序列，利用残差序列对不同分析中心的钟差值进行定权，从而求得2家分析中心的加权均值作为钟差综合值，以此提高不同分析中心钟差产品之间的一致性。实验结果发现：

1)不同分析中心的轨道径向和钟差相对偏差存在明显的周期项，并且轨道径向与钟差呈现负相关的特征，这说明不同分析中心的轨道和钟差产品存在一致性问题。

2)以SHA&WHU为例，分析发现BDS、GPS、GLONASS有明显的12h和24h周期项，Galileo有明显的12h周期项，但24h周期项不明显；除此之外，BDS还有48h、8h和6h周期项，GLONASS还有明显的8h周期项。4个系统钟差相对偏差主周期项存在差异，BDS和Galileo的主周期项均约12h，而GPS和GLONASS的主周期项约24h。

3)将本文提出的钟差综合模型得到的钟差综合值与ISC钟差产品对比发现，钟差综合值可以明显提高各分析中心的钟差产品一致性。

4)本文提出的方法仅对不同分析中心的钟差产品进行了综合，在一定程度上提高了各分析中心的一致性，但并未对轨道产品的一致性进行改善。故接下来将研究如何对不同分析中心的轨道进行产品综合，以提高轨道的一致性。