顾及星座稳定性及综合成本的低轨导航星座优化设计方法

贺备，蔡昌盛，潘林，蔡成林

(1.中南大学 地球科学与信息物理学院,长沙 410083；2.湘潭大学 自动化与电子信息学院,湖南 湘潭 411100)

0 引言

全球卫星导航系统(GNSS)已经在导航、定位和授时(PNT) 领域发挥了巨大的作用，但GNSS 自身的可靠性和可用性较为脆弱[1]，如在进行GNSS 精密单点定位(PPP)时收敛时间过长，而且由于GNSS 轨道高度高，地面接收站所接收到的信号较弱，特别是在遮蔽环境下影响更为严重.相比而言，低轨道地球卫星(LEO) 的轨道高度较低，信号在传播过程中损失较少，地面接收信号强.此外，LEO 运行速度快，卫星的快速运动有助于星座空间几何形态的快速变化，可以促进PPP 收敛速度的提升.杨元喜院士[2]提出综合PNT 系统和弹性PNT 概念，并将低轨卫星增强技术作为PNT 体系中的核心技术.近年来，低轨卫星技术发展迅速，国内外机构相继提出低轨卫星发展计划.

低轨卫星对GNSS 进行导航增强的前提是具有分布合理的星座构型.基于此，有不少学者开展了星座设计研究.GE 等[3]从轨道倾角、卫星数、轨道平面数等方面开展星座设计，并将不同倾角的LEO 星座组合在一起与GNSS 联合进行PPP 定位.HE 等[4]为增加可见卫星数沿纬度分布的均匀性，设计了不同轨道倾角组合的混合星座.田野等[5]推导了低轨卫星轨道高度与可视球冠以及太空垃圾的关系，提出精度衰减因子(DOP) 值较小的不同倾角轨道组合方案.上述研究工作均采用分析枚举法设计低轨星座构型，难以衡量星座设计构型是否达到最优.徐哲宇等[6]基于Flower 星座构型并结合差分进化算法进行了轨道参数优化，设计了一种区域导航增强的星座方案.GUAN 等[7]基于遗传算法与非支配遗传算法针对多目标优化进行了混合Walker 星座设计.MA 等[8]设计了综合多种星座构型的混合星座，在固定卫星颗数以及仰角的条件下采用遗传算法求取最优组合.上述研究工作采用优化算法进行星座设计，但他们在优化设计过程中未顾及卫星综合成本以及混合星座的稳定性.谢恺等[9]在星座设计中粗略分析了星座设计的发射成本因子，然而没有考虑到卫星制造成本，无法全面衡量星座设计的综合成本.YANG 等[10]提出在设计混合星座时需要考虑轨道面之间的进动角速度影响，从而使得混合星座具有稳定构型.

本文同时顾及星座稳定性及综合成本进行低轨导航星座的优化设计.以Walker 星座作为基本构型，在保证混合星座稳定性的基础上顾及综合成本及导航性能，利用遗传算法开展了低轨混合星座优化设计.

1 星座设计方法

1.1 遗传算法

星座设计的目的是将功能相似的多颗卫星分布在不同的轨道上，从而实现特定任务.目前而言，进行星座设计的主要方法包括几何解析法、仿真比较分析法以及优化算法[11].采用遗传算法等优化算法，可以顾及多目标任务，在空间范围内搜索最优的星座设计参数，能够弥补传统的几何解析法以及仿真比较法的不足，从而实现低轨星座的最优化设计.

遗传算法借鉴达尔文的进化论与自然选择学说，实际上是一种随机全局搜索的优化方法.遗传算法采用适者生存的原则，将问题编码成为二进制串染色体生成初始种群，通过设置适应度函数，保留种群中的最优个体，在此基础上针对编码个体进行选择、交叉及变异等操作得到新的种群，不断优胜劣汰直至得到最优解[12].相较于传统算法而言，遗传算法采用面对面的全局搜索方法，避免陷入优化过程中局部最优的情况，且具有较高的搜索能力和极强的鲁棒性[13].本文使用遗传算法处理附有整数约束条件的低轨星座优化问题.

1.2 Walker 星座构型

Walker 星座是一种常用的星座构型，具有很好的全球对称均匀分布特性，在实际星座设计中应用广泛.Walker 星座可由T、P、F三个参数确定[12].其中，T为星座中的卫星总数，P为星座的轨道面数，F为相位因子，用来确定相邻轨道间的相位差，F的取值范围为(0～P-1).

将第一个轨道面的第一颗卫星定义为种子卫星，确定种子卫星的轨道参数即可计算得到Walker 星座中所有卫星的轨道参数，式(1)给出了轨道参数的计算方法[14].

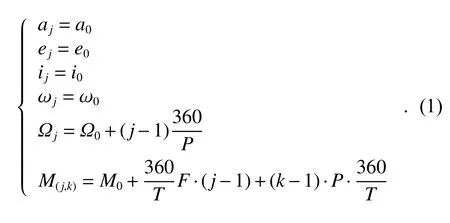
a0、e0、i0、ω0、Ω0、M0分别表示种子卫星的半长轴、偏心率、倾角、近地点角距、升交点赤经以及平近点角.在上述参数中，半长轴和偏心率决定了轨道的形状，轨道倾角与升交点赤经决定了轨道平面的位置，近地点角距决定轨道半长轴方向，平近点角决定了卫星相对于时间的位置.j表示第j个轨道面，(j,k)表示第j个轨道面上的第k个卫星，由上式可计算第j个轨道面上第k颗卫星的轨道参数.

1.3 星座综合成本计算

在设计低轨导航增强星座过程中，考虑导航性能增强指标如可见卫星数目以及分布均匀性的同时，也应该考虑综合成本.以Starlink 为例，完成62 颗卫星的组网布设需要花费成本费用高达6 200 万美元[15]，由此可知星座的成本费用是非常巨大的，所以在保证星座性能的同时应尽可能降低成本.

星座综合成本可分为星座制造成本、发射成本以及维护成本.星座成本模型很难具体定量分析，到目前为止还没有完善的星座成本模型.但已有研究表明，星座综合成本与卫星数、轨道平面数、轨道高度以及轨道倾角有关[9].卫星数越多则制造与维护成本越大；卫星发射通常采用一箭多星技术使得卫星落在同一轨道面上，所以发射成本会随轨道面的增加而增加；轨道高度越高，相应需要的发射能量越大；轨道倾角增加时，借助地球自转能量越少，同样增加了发射成本.基于此，本研究将卫星综合成本因子表达为

式中：P为轨道面个数；P0为轨道面数下限；i为轨道倾角，单位为rad；h为轨道高度；h0为轨道高度下限；T为卫星数目；T0为卫星数目下限.值得注意的是，该卫星综合成本因子只表示在一个具体问题中不同方案的相对成本.

1.4 星座优化目标函数设置

本文旨在设计导航增强的低轨星座，对于导航定位而言，必须实现可见卫星数目大于4，在此基础上可见卫星越多，观测值的冗余度越高，导航定位的可靠性和精度也越高，同时可见卫星分布越均匀，越有利于提升导航定位的精度.所以对设计星座的性能评价可分为全球平均可见卫星数、可见卫星分布的均匀程度以及星座综合成本因子三个指标.

由于Walker 星座构型为全球均匀对称分布，其在全球的可见性也是均匀分布的.为简化计算且考虑到全球经济以及人口分布大部分在北半球，我们选取经度为0°的经线，在纬度方向每隔2.5°建立高度为25 m 的虚拟观测站，这样共建有37 个虚拟观测站，设置截止高度角为7°.目标函数为

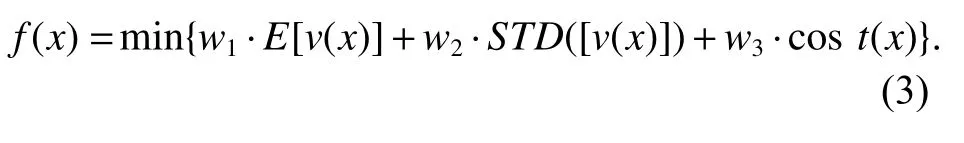
式中：E[v(x)]为全球平均可见卫星数；STD([v(x)]) 为全球可见卫星数标准偏离值，即全球可见卫星数STD值，用于衡量可见卫星分布均匀程度；c ost(x) 为综合成本因子，其中w1、w2、w3表示各部分所占权重，将w1、w2、w3分别设置为-0.2、0.7、0.1，这样的定权方式表明：可见卫星数目越多，分布越均匀，星座综合成本越少，则认为星座配置最优.

2 实验结果与分析

2.1 基于遗传算法的铱星星座优化

铱星是以Walker 为星座构型的低轨卫星星座，轨道倾角为86.4°，轨道高度为780 km，通过STK 与MATLAB 互联对铱星轨道进行积分并输出铱星的空间三维构型，如图1 所示.

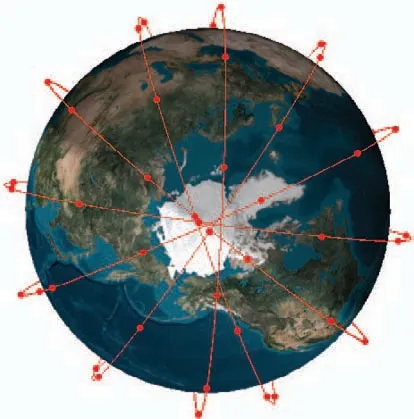
图1 铱星三维构型

采用1.4 节星座优化的目标函数，顾及综合成本并基于遗传算法对铱星星座进行优化设计，设置决策变量为 [i,F]，其中i表示轨道倾角，F表示相位因子，决策变量取值范围如表1 所示.

表1 铱星星座决策变量范围

由于实验中采取了整数约束，染色体编码采用实数编码，形式为

在种群繁衍和进化的过程中，适应度最强的个体直接存活至下一代而不做任何改变的精英个体数目设置为2.此外，为了求解混合整数约束的最优化问题，使用了工具箱中的整数GA 求解器，采用等级适应度函数排序，随机均匀选择算子.交叉算子选择GA 求解器中的约束依赖模式，根据优化函数的约束选择不同的函数，交叉概率设置为0.8，变异算子采用自适应变异函数，适应度大的个体变异概率小，适应度小的个体变异概率相对较大.实验中采取了整数约束，遗传算法试图使惩罚值函数达到最小而不是目标函数最小，程序内部将使用惩罚函数值代替目标函数值，对于满足约束条件的解，其惩罚值就成为目标函数，而对于不满足约束条件的解，其惩罚值等于满足约束条件的最大目标函数值加上相应的违例惩罚项以降低其适应度[8].

遗传算法中合适的初始种群大小和遗传代数对于提高计算效率和有效寻求最优解很重要，如果初始种群和遗传代数太小，算法可能无法有效地搜索空间中的最优解，如果初始种群和遗传代数过大，则会降低计算效率，增加搜索时间.在本次实验中设置种群大小为40，遗传代数为50.

成本因子定义为

图2 显示了对铱星星座优化50 代的平均和最佳惩罚值轨迹图.从图2 中可以看出，随着种群的选择、交叉、变异、繁殖，种群的适应度逐渐增强，相应的惩罚值逐渐趋于稳定.

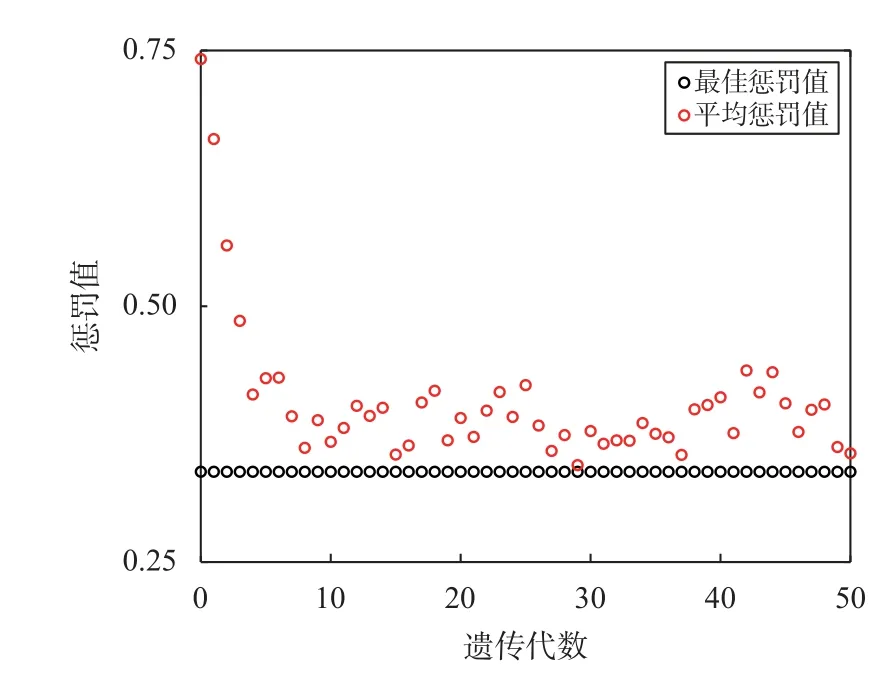
图2 遗传算法搜索铱星星座最优解过程

最终确定优化后的星座轨道倾角为70°，相位因子为3.优化后的星座三维构型如图3 所示，表2 给出了铱星优化前后的星座性能统计结果.

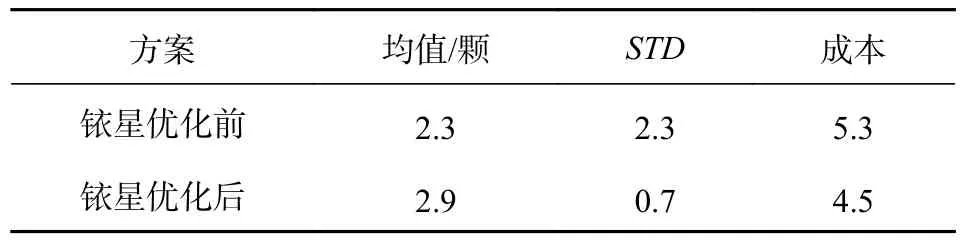
表2 铱星优化前后的星座性能对比

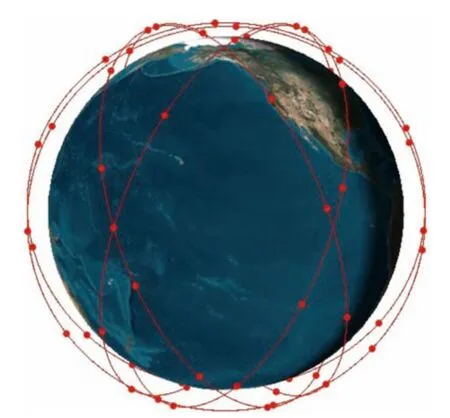
图3 优化后的铱星星座三维构型

图4 给出了铱星优化前后可见卫星数随纬度的变化情况.由于铱星轨道倾角接近90°，所以高纬度地区铱星的可见卫星数目大于优化后的星座.在65°以下的区域，优化后的可见卫星数显著优于优化前的铱星，而且优化后的可见卫星数整体上沿位置纬度变化更为平缓.计算结果表明，无论可见卫星数、STD值还是综合成本因子较优化前的铱星星座均有明显改善，全球可见卫星数均值由2.3 颗增至2.9 颗，可见卫星数STD由2.3 降至0.7，综合成本因子由5.3 降至4.5，证明了本设计方法的有效性.

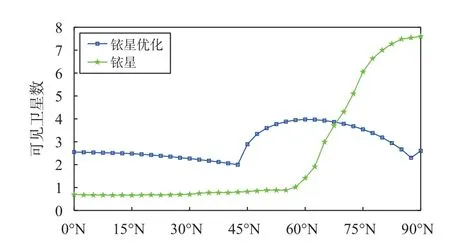
图4 铱星优化前后星座随纬度变化的可见卫星数

2.2 基于遗传算法的混合星座设计

2.2.1 星座构型稳定性

当卫星星座的高度和倾角不同时，由于地球的非球形摄动力引起的轨道面进动产生差异会导致不同高度和倾角构成的星座不稳定，从而改变星间以及卫星和地球之间的几何关系[16]，无法保证星座能否按照设计方案准确运行.因此，混合星座优化的前提是星座构型具有稳定特性.

在设计星座轨道高度时，需要考虑的不仅是覆盖性能，更需要考虑空间环境，如太空垃圾分布、辐射粒子以及太空引力等实际因素.文献[7]使用STK 分析了500～1 100 km 的大气阻力对轨道因素的影响，并指出当轨道高度低于900 km 时大气阻力显著增加.当轨道高度高于1 500 km 时会受到范艾伦辐射带的影响，所以适宜的轨道高度范围为900～1 500 km.

低倾角和高倾角的取值范围分别在(0°，45°)、(45°，90°)，这样能够使得倾角较小的星座增加赤道附近地区的卫星可见度，倾角较大的星座可以更好地覆盖高纬度地区.

为了保持星座稳定构型，必须在相同的进动速度下选择轨道[10].式(6) 给出了轨道面进动速度计算公式

式中：Ω 为轨道面进动速度；Re为地球半径；e为偏心率；a为轨道高度；ω 为卫星的角速率；J2=1.086×103.

在轨道高度范围和轨道倾角范围内进行遍历求解轨道面进动速度，轨道高度精度设置为1 km，轨道倾角精度设置为1°.由以上分析可知，当低倾角星座与高倾角星座轨道进动速度相同时即可确定相对应的轨道高度和轨道倾角，具体构型设计如表3所示.

表3 混合星座轨道倾角与高度构型设计

2.2.2 混合星座优化

将混合星座决策变量设置为[P1,N1,F1,P2,N2,F2]，P为轨道面数，N为单个轨道面上的卫星数，F表示相位因子，且下标表示组合星座中的子星座，决策变量取值范围如表4 所示.

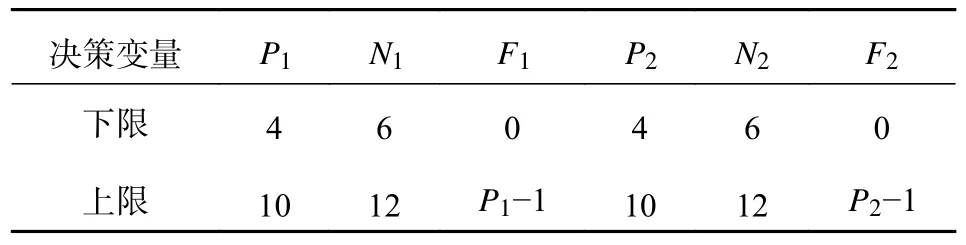
表4 决策变量取值范围

染色体编码形式为

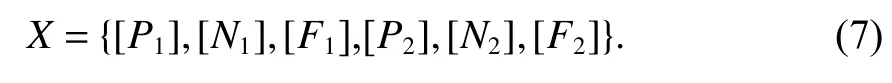
在种群繁衍和进化的过程中，适应度最强的个体直接存活至下一代而不做任何改变的精英个体数目设置为3，其余处理策略与2.1 节中策略一致.

综合成本因子表示为

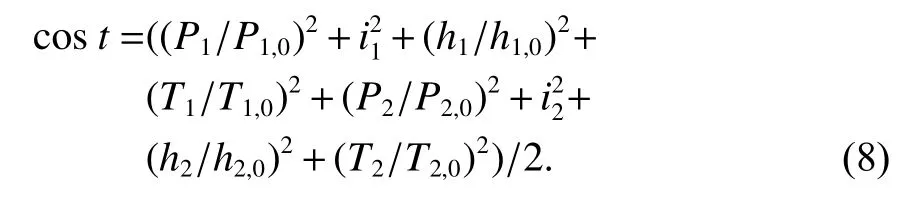
式中：P为轨道面个数；P0为轨道面数下限；i为轨道倾角，单位为rad；h为轨道高度；h0为轨道高度下限；T为卫星数目；T0为卫星数目下限；下标1、2 分别为混合星座中的两种不同的星座构型.

目标函数为

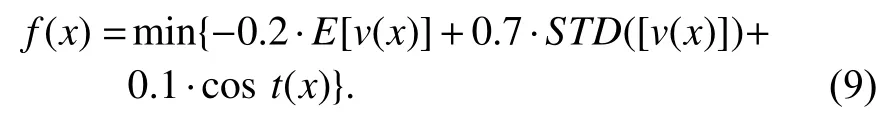
在遗传算法中设置初始种群为60，遗传代数为50.图5 显示了对混合星座50 代的平均及最佳惩罚值轨迹图，从图5 中可以看出，随着种群的选择、交叉、变异、繁殖，种群的适应度逐渐增强，相应的惩罚值减少，直至收敛.

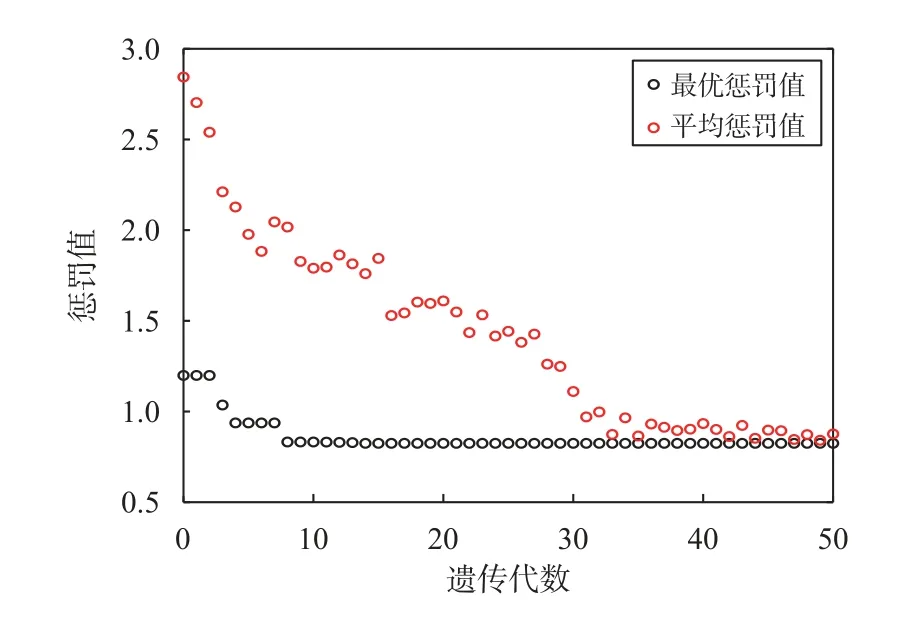
图5 遗传算法搜索混合星座最优解过程

通过遗传算法搜索最优解后得到轨道高度为1 360 km、轨道倾角为160 的Walker24/4/1 星座与轨道高度为975 km、轨道倾角为620 的Walker35/5/2星座.图6 给出了优化后的低轨混合星座(Walker24/4/1 与Walker35/5/2)三维构型.为进一步验证混合星座对GNSS 的增强性能，图7 给出了北斗/低轨混合星座的三维构型，并分别对低轨混合星座、北斗星座以及北斗/低轨混合星座进行性能评估.

图6 优化后的低轨混合星座三维构型

图7 北斗/低轨混合星座三维构型

表5 为低轨混合星座与北斗星座以及北斗/低轨混合星座的可见卫星数以及STD值，由于在设计混合星座过程中就已经顾及星座成本，所以此处没有对成本因子进行评估.将组合后的星座与北斗星座相比较，全球可见卫星数均值由6.9 颗增至9.3，可见卫星数标准差由1.1 降至0.4.可见卫星数沿纬度变化如图8 所示.本文主要针对于低轨卫星对于现有北斗系统的导航增强，所以即使混合低轨星座可见卫星数目小于4，虽然不能进行单独的导航定位，但是在与北斗系统混合之后，增加了可见卫星数，降低了STD值，能够起到导航增强的作用.

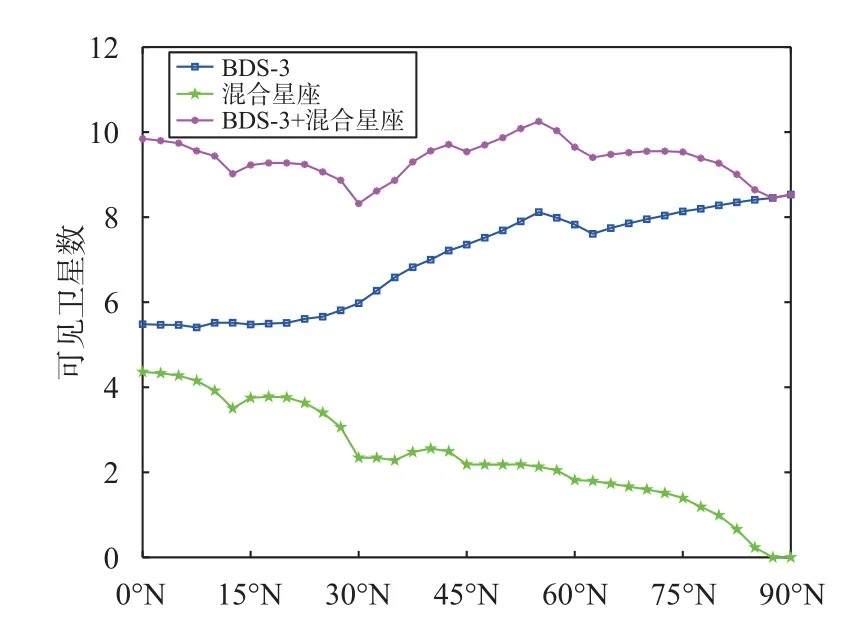
图8 不同星座可见卫星数沿纬度位置变化分布

表5 不同星座性能

3 结束语

本文通过顾及星座稳定性及综合成本，基于遗传算法对铱星星座以及混合星座进行了优化设计.在顾及导航性能以及综合成本的基础上，设计目标函数，采用与铱星相同的轨道构型，对轨道倾角、相位因子进行搜索，得到倾角70°，相位因子为3 的优化后的铱星星座构型，与优化前的铱星星座相比，全球平均可见卫星数由2.3 增至2.9，STD值由2.3 降至0.7，同时成本因子由5.3 降至4.5，验证了本文方法的有效性.在保证星座构型稳定性的条件下，确定高倾角与低倾角混合星座的轨道高度和轨道倾角，固定Walker星座的相位因子为0，利用遗传算法得到轨道高度为1 360 km、倾角为16°的Walker 24/4/1 星座与轨道高度为975 km、倾角为62°的Walker 35/5/2 星座.将设计得到的低轨混合星座与北斗星座组合后，与北斗星座相比平均可见卫星数由6.9 增至9.3，STD值由1.1 降至0.4.在未来的星座优化设计过程中应该考虑到更多的实际因素，如星座运行过程中是否存在碰撞风险、卫星轨道是否存在衰减可能等.