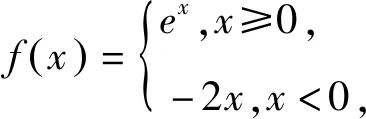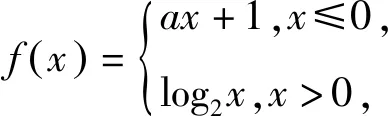探析复合函数零点问题的三种类型及求解策略

苏艺伟

(福建省龙海第一中学新校区 363100)

对于复合函数的零点问题,常常采用换元的方法求解.通常将表达式中的某部分换成t,看成是函数y=g(t)与函数t=f(x)复合而成,最终转化为研究直线y=t与曲线y=f(x)图象的交点个数问题.此类题型体现了函数与方程思想,能够较好地考查学生的数形结合能力,逻辑推理、分析问题与解决问题的能力,经常出现在选填压轴试题当中,深受命题者亲赖.

类型1 函数f(x)中将某个整体替换成t.

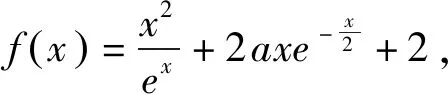
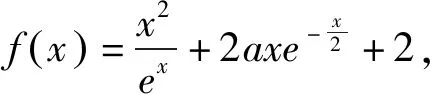
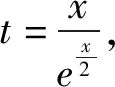
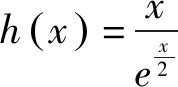
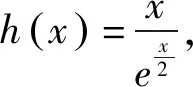
令h′(x)=0,得x=2.

又h(0)=0,故h(x)的图象如图1所示.

图1

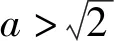
对于方程t2+2at+2=0,有Δ=4a2-8.

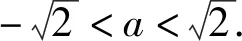
此时方程t2+2at+2=0无解,不符合题意;

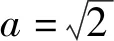
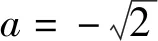
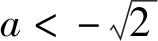
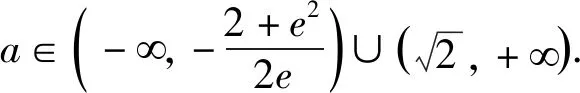
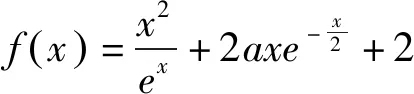
类型2 含f2(x)的表达式中将f(x)替换成t.

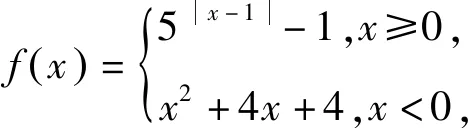
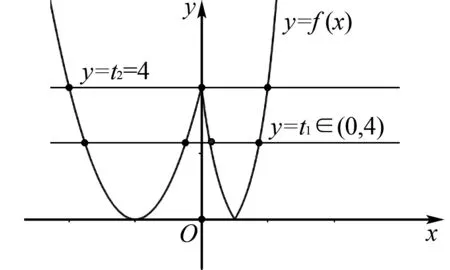
图2

解析令t=f(x),则关于t的方程t2-(2m+1)t+m2=0存在两个实根t1,t2.

不妨设t1

故关于x的方程f2(x)-(2m+1)f(x)+m2=0有7个不同的实根就是函数y=f(x)图象与直线y=t1,y=t2交点个数之和为7.

如图2所示,要使得交点个数和为7,则

0

将t2=4代入方程t2-(2m+1)t+m2=0,

得m=2或m=6.

又t1t2=m2<16,故m=2.

分析由于方程f2(x)-(2m+1)f(x)+m2=0含有f2(x),故将f(x)替换成t,转化为研究方程t2-(2m+1)t+m2=0实根的分布情况以及直线y=t与曲线y=f(x)图象交点个数.

类型3 含f[f(x)]的表达式中将f(x)替换成t.

图3 图4

对于方程②,函数y=f(t)图象与直线y=-k交点横坐标t的取值范围如图3所示.

当-k≤0,即k≥0时,y=f(t)图象与直线y=-k无交点;

当0<-k<1，即-1

当1<-k

当-k≥e,即k≤-e时,交点横坐标t1<0,t2≥1，对应图4中的2个交点.

综合上述分析,当k≥-1时,关于x的方程f[f(x)]+k=0的零点个数有0个;

当-e

当k≤-e时,关于x的方程f[f(x)]+k=0的零点个数有2个.

分析由于方程f[f(x)]+k=0含有f[f(x)],故将f(x)替换成t,转化为研究方程f(t)=-k以及直线y=t与曲线y=f(x)图象交点个数.

图5 图6

A.无论a为何值,均有2个零点

B.无论a为何值,均有4个零点

C.当a>0时,有3个零点, 当a<0时,有2个零点

D.当a>0时,有4个零点, 当a<0时,有1个零点

当a>0时,先考虑方程④,函数y=f(t)图象与直线y=-1相交于A,B两点,对应的横坐标分别为t1,t2.如图5所示.显然t1<0,0

再考虑方程③,如图6所示,函数y=f(x)图象与直线y=t1的交点个数有2个,函数y=f(x)图象与直线y=t2的交点个数有2个.

故当a>0时,函数y=f[f(x)]+1有4个零点.同理可知,当a<0时,有1个零点.

分析由于方程f[f(x)]+1=0含有f[f(x)],故将f(x)替换成t,转化为研究方程f(t)=-1以及直线y=t与曲线y=f(x)图象交点个数.

通过对上述几道试题的分析,不难发现此类复合函数零点问题,既注重基础,又兼顾能力,较好地体现了中国高考评价体系提出的基础性、综合性、应用性、创新性要求.此类试题的解决思路较为固定,往往采用换元的方法,结合图形,观察一条直线与一条曲线图象交点的个数.然而法无定法,试题千变万化,在实际解题中,我们必须根据题目所给出的条件灵活地选择合适的方法,方能以不变应万变,实现解题的最优化.