无相邻3-圈平面图的邻点可区别边染色
蔡洪锋, 黄丹君
(浙江师范大学 数学与计算机科学学院,浙江 金华 321004)
0 引 言

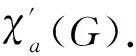
Zhang等[1]在2002年提出图的邻点可区别边染色这一概念,并对一些特殊图类(树、路、圈、完全图、完全二部图等)的邻点可区别边色数进行了刻画.基于这些结果,他们给出了关于图的邻点可区别边染色问题的猜想.


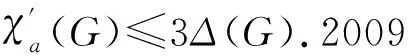
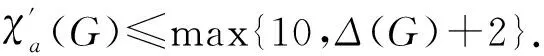
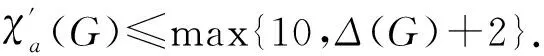
1 定理1的证明
假设G是定理1中关于边数达到最小的一个极小反例.显然,G是连通的.先分析G的结构性质,再运用权转移方法得出矛盾,从而定理1得证.令T(G)=max{10,Δ(G)+2},C={1,2,…,T(G)}表示颜色集合.显然|C|≥10.
断言1[15]图G中1-点不与5--点相邻.
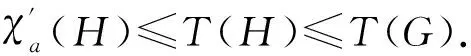
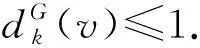
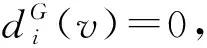
注2设uv∈E(G)为G中的轻k-边,k∈{2,3,4}.若H=G-uv存在一个T(G)-avd-边染色φ且Cφ(u)≠Cφ(v),则|C(Cφ(u)∪Cφ(v))|≥10-2(k-1)≥4.由断言2知,∃α∈C(Cφ(u)∪Cφ(v)),使得边uv可染α色且满足u不与NG(u)中的点冲突,v不与v的邻点冲突.因此,可以将φ扩染为G的一个T(G)-avd-边染色.
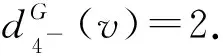
证明记NG(v)={v1,v2,…,vk},NG(v1)={v,v2,u1,u2}且NG(v2)={v,v1,w1,w2}.令H=G-v1v2.由注1知,H有一个T(G)-avd-边染色φ.设φ(vvi)=i,i∈[1,k].
先证:若G中存在(4,4,k)-圈v1v2vv1,则k≥7.用反证法.假设k≤6.由断言2和断言3知,k=6.由注2知,Cφ(v1)=Cφ(v2).不妨设Cφ(v1)=Cφ(v2)={1,2,a}且a∈[3,7].可以用{8,9,10}中的任意一种颜色改染vv1或vv2,导出v的6个不同的颜色集合,而v至多只有4个冲突点,所以必存在一种改染方式φ′,使得v不与其邻点产生冲突且Cφ′(v1)≠Cφ′(v2).由注2知,φ可以扩染为G的一个T(G)-avd-边染色.矛盾.
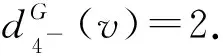
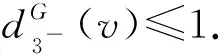
断言6设dG(v)=7,则
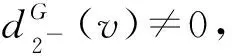
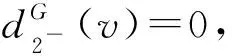
3)v不与(3,3,7)-圈关联.
证明令NG(v)={v1,v2,…,v7}.由文献[15]的断言6知,1)成立.
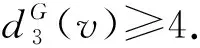
3)用反证法.假设v与(3,3,7)-圈关联.设dG(v1)=dG(v2)=3且v1v2∈E(G).令H=G-v1v2.由注1知,H有一个T(G)-avd-边染色φ.设φ(vvi)=i,i∈[1,7].由注2知,Cφ(v1)=Cφ(v2)={1,2}.用{8,9,10}中的任意一种颜色改染vv1或vv2,得到v的6个不同的颜色集合.而v至多只有5个冲突点,所以必存在一种改染方式φ′,使得v不与其邻点产生冲突且Cφ′(v1)≠Cφ′(v2).由注2知,φ可以扩染为G的一个T(G)-avd-边染色.矛盾.断言6证毕.
断言7设dG(v)=k且k≥8,则

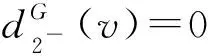
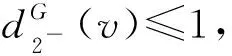
证明记NG(v)={v1,v2,…,vk}.
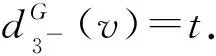
2)设dG(v1)=dG(v2)=3且v1v2∈E(G).令H=G-v1v2,由注1知,H有一个T(G)-avd-边染色φ.设φ(vvi)=i,i∈[1,k].由注2知,Cφ(v1)=Cφ(v2)={1,2}.
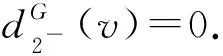
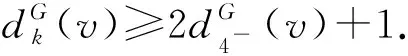
3)设dG(v1)=dG(v2)=4且v1v2∈E(G).令H=G-v1v2,由注1知,H有一个T(G)-avd-染色φ.设φ(vvi)=i,i∈[1,k].由注2知,Cφ(v1)=Cφ(v2)={1,2,a}.
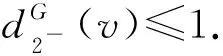
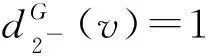
令H为G中删去所有2--点所得到的点数最多的一个连通分支,因此,δ(H)≥3且H是无相邻3-圈的平面图.根据断言1和断言5~断言7可推断出dG(v)和dH(v)的关系如表1所示.

表1 dG(v)和dH(v)之间的关系
断言81)若dH(v)=k且3≤k≤4,则dG(v)=dH(v);
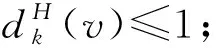

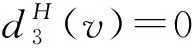
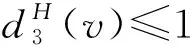
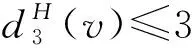
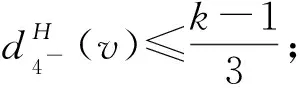
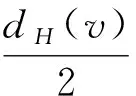
9)任意3-面f至少关联1个5+-点v.
证明根据表1和断言1~断言3可知,1)~3)和9)显然是正确的.
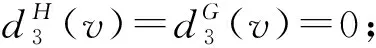
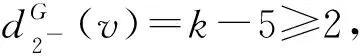
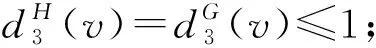
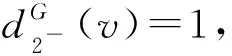
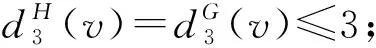
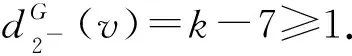
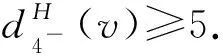
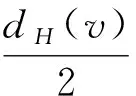
下面利用权转移方法推出矛盾.首先,对任意x∈V(H)∪F(H),定义初始权函数w(x)=dH(x)-4.根据欧拉公式|V(H)|-|E(H)|+|F(H)|=2,有
下面定义适当的权转移规则.在权转移过程中,总权和保持不变.记新的权函数为w′(x),x∈V(H)∪F(H).若能证明对任意x∈V(H)∪F(H),有w′(x)≥0,则有如下矛盾:
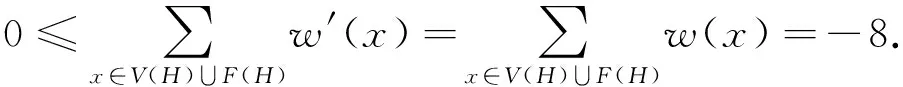
因此,图H不存在,从而极小反例图G不存在,即定理1成立.
定义如下权转移规则:
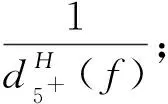
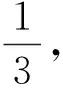
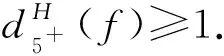
下面证明对∀v∈V(H),有w′(v)≥0.
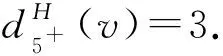
设dH(v)=4.则w′(v)=4-4=0.
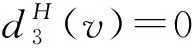
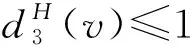
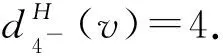
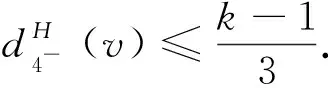
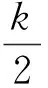
因此,完成了定理1的证明.
2 结 语