von Neumann 代数上保持混合三重η-*-积的非线性映射
张芳娟, 朱新宏
(1.西安邮电大学理学院, 西安 710121; 2.西安现代控制技术研究所, 西安 710065)



1) 如果对所有B∈M有ABP=0,那么A=0.
2) 如果η是非零常数且对任意T∈M有(PT(I-P))·ηA=0, 那么A(I-P)=0.
引理3[6]设M是von Neumann代数,A∈M, 若对所有的B∈M, 有AB+BA*=0,则A=-A*∈Z(M).
1 可加性
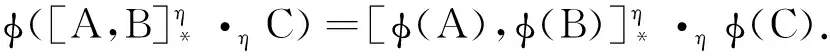

断言1φ(0)=0.
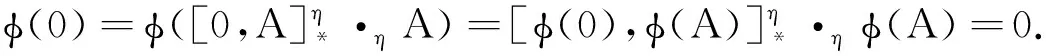
断言2任取A12∈M12,A21∈M21,则φ(A12+A21)=φ(A12)+φ(A21).

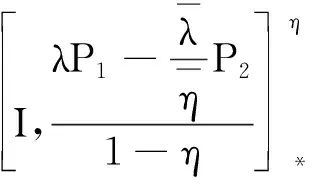
断言3设i,j∈{1,2},若i≠j,Aii∈Mii,Aij∈Mij,Ajj∈Mjj,则φ(Aii+Aij)=φ(Aii)+φ(Aij),φ(Ajj+Aij)=φ(Ajj)+φ(Aij).


断言4设i,j∈{1,2},若i≠j,Aii∈Mii,Aij∈Mij,Aji∈Mji,则φ(Aii+Aij+Aji)=φ(Aii)+φ(Aij)+φ(Aji).

由此可得Xij=Aij,Xji=Aji,Xjj=0,则X=Xii+Aij+Aji.

由此可得Xii=Aii.
断言5任取A11∈M11,A12∈M12,A21∈M21,A22∈M22,则φ(A11+A12+A21+A22)=φ(A11)+φ(A12)+φ(A21)+φ(A22).

由此可得X11=A11,X12=A12,X21=A21.类似可得X22=A22.
断言6设i,j∈{1,2},若i≠j,Aij,Bij∈Mij,则φ(Aij+Bij)=φ(Aij)+φ(Bij).


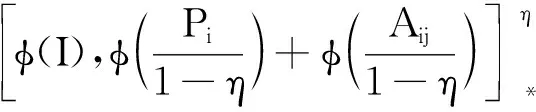
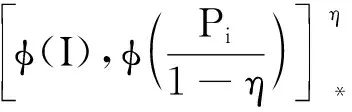
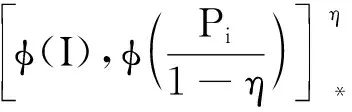
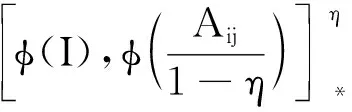
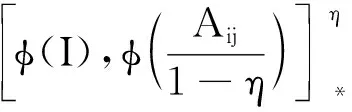
则φ(Aij+Bij)=φ(Aij)+φ(Bij).
断言7设i,j∈{1,2},若i≠j,Aii,Bii∈Mii,则φ(Aii+Bii)=φ(Aii)+φ(Bii).

由此可得Xjj=Xji=Xij=0.
任取Cij∈Mij,i≠j,由断言6得

由此可得(Xii-Aii-Bii)Cij=0.即对所有的C∈M,有(Xii-Aii-Bii)CPj=0.由引理2得Xii=Aii+Bii.所以φ(Aii+Bii)=φ(Aii)+φ(Bii).
断言8φ是可加的.
由断言5~7得φ是可加的.
2 线性
若η=-1,则有下面定理.
定理2设M和N是两个von Neumann代数, 其中至少有一个无中心交换投影.若φ是从M到N的双射并且满足对所有A,B,C∈M有φ([A·B,C]*)=[φ(A)·φ(B),φ(C)]*,则下列结论成立:φ(I)φ是线性*-同构和共轭线性*-同构的和,其中φ(I)是N中自伴中心元且φ(I)2=I.
证明分下面几步完成.
第一步1) 任取A∈M,则φ(A)*=φ(A)当且仅当A*=A;
2)φ(Z(M))=Z(N).
由于φ是满射, 所以存在B∈M,使得φ(B)=I.则对任意A∈M有
0=φ([iI·A,B]*)=[φ(iI)·φ(A),I]*=φ(iI)(φ(A)-φ(A)*)+(φ(A)-φ(A)*)φ(iI)*.
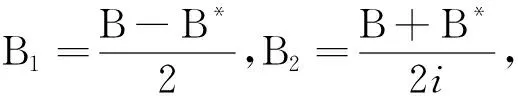
φ(iI)=-φ(iI)*∈Z(N).
(1)
类似可得φ-1(iI)∈Z(M).
令A=A*∈M且φ(B)=I.则
0=φ([B·A,φ-1(iI)]*)=[I·φ(A),iI]*= 2iφ(A)-2iφ(A)*.
由此可得φ(A)=φ(A)*.同理若φ(A)=φ(A)*,则
0=φ-1([φ(I)·φ(A),φ(iI)]*)= [I·A,iI]*=2iA-2iA*.
所以A=A*,因此φ双边保持自伴元.
任取Z∈Z(M)且φ(B)=I.对所有A=A*∈M,有
0=φ([B·A,Z]*)=[I·φ(A),φ(Z)]*= 2(φ(A)φ(Z)-φ(Z)φ(A)*).

第二步1)φ(iI)*=-φ(iI),φ(I)2=I;
2)任取A∈M,则φ(A*)=φ(A)*.
由第一步和式(1)得
4φ(iI)=φ([I·iI,I]*)=[φ(I)·φ(iI),φ(I)]*=
2φ(I)2(φ(iI)-φ(iI)*)=4φ(I)2φ(iI).
即
φ(iI)=φ(I)2φ(iI).
(2)
对所有A=A*∈M,由第一步和式(1)得
-4φ(A)=φ([A·iI,iI]*)= [φ(A)·φ(iI),φ(iI)]*=4φ(iI)2φ(A).

φ(iI)2=-I.
(3)
由式(2)和式(3)得
φ(I)2=I.
(4)
任取A∈M, 因为φ(I)是自伴中心元,所以2φ(A-A*)=φ([I·A,I]*)=[φ(I)·φ(A),φ(I)]*=2φ(I)2(φ(A)-φ(A)*).联合式(4)得φ(A)*=φ(A)*.
定义映射ψ:M→N,对所有A∈M, 有ψ(A)=φ(I)φ(A).ψ有下面性质.
第三步1)ψ是可加的双射, 对所有A,B,C∈M,满足ψ([A·B,C]*)=[ψ(A)·ψ(B),ψ(C)]*;
2)ψ(I)=I,ψ(iI)2=-I,ψ(iI)*=-ψ(iI),ψ(Z(M))=Z(N);
3) 对所有A∈M, 有ψ(A*)=ψ(A)*;
4)P是M中投影当且仅当ψ(P)是N中投影.
1)、2)、3)易得,下面证明4).若P是M中投影,一方面
4ψ(iP)=ψ([I·iI,P]*)= [I·ψ(iI),ψ(P)]*=4ψ(iI)ψ(P).
另一方面,
4ψ(iP)=ψ([I·iP,P]*)= [I·ψ(iP),ψ(P)]*=4ψ(iI)ψ(P)2.
所以,ψ(iI)ψ(P)=ψ(iI)ψ(P)2.由ψ(iI)2=-I得ψ(P)=ψ(P)2.所以,ψ(P)是N中的投影.
下面的证明不需要N无中心交换投影的条件,所以上面的结果对ψ-1成立.若ψ(P)是N中的投影,则P=ψ-1(ψ(P))是M中的投影.

第四步ψ(Mij)=Nij,ψ(Mii)⊆Nii,1≤i≠j≤2.
任取Aij∈Mij,有
由此可得Qiψ(Aij)Qi=Qjψ(Aij)Qj=Qjψ(Aij)Qi=0, 则ψ(Mij)⊆Nij.再用同样方法考虑映射ψ-1,所以ψ(Mij)=Nij.
任取Aii∈Mii,由
0=ψ([Pj·iI,Aii]*)=[Qj·ψ(iI),ψ(Aii)]*= 2ψ(iI)(Qjψ(Aii)+ψ(Aii)Qj),
得Qiψ(Aii)Qj=Qjψ(Aii)Qi=Qjψ(Aii)Qj=0,则ψ(Mii)⊆Nii.
第五步ψ是可乘的.

由ψ(Aij)ψ(Bii)*=0,i≠j得
任取Dij∈Nij,由第四步得Cij=ψ-1(Dij)∈Mij,所以
ψ(AiiBii)Dij=ψ(AiiBiiCij)=ψ(Aii)ψ(BiiCij)=ψ(Aii)ψ(Bii)Dij.

计算得
ψ(AijBji)-ψ(BjiAij)=ψ([Aij·I,Bji]*)= [ψ(Aij)·I,ψ(Bji)]*=ψ(Aij)ψ(Bji)-ψ(Bji)ψ(Aij).
所以,
ψ(AijBji)=ψ(Aij)ψ(Bji),ψ(BjiAij)=ψ(Bji)ψ(Aij).
任取Dji∈Nji,由第四步得Cji=ψ-1(Dji)∈Mji,所以,
ψ(AijBjj)Dji=ψ(AijBjjCji)=ψ(Aij)ψ(BjjCji)=ψ(Aij)ψ(Bjj)Dji.

第六步存在中心投影E∈M, 使得ψ限制在ME上是线性映射,ψ限制在M(I-E)上是共轭线性映射.
任取有理数q,有ψ(qI)=qI.取M中正元A,则存在自伴元B∈M使得A=B2.由第五步得ψ(A)=ψ(B)2,由ψ(B)是自伴元得ψ(A)是正元,所以ψ保持正元.
设λ∈, 取两个有理数列{an},{bn}使得an≤λ≤bn和对所有的n都成立.由anI≤λI≤bnI得anI≤ψ(λI)≤bnI.取极限得ψ(λI)=λI.因此对所有A∈M,有ψ(λA)=ψ(λI)ψ(A)=λψ(A),则ψ是实线性的.

ψ(iAE)=ψ(A)ψ(E)ψ(iI)=ψ(A)ψ(E)i(2F-I)=iψ(A)F=iψ(AE)
和
ψ(iA(I-E))=ψ(A)ψ(I-E)ψ(iI)= -iψ(A)(I-F)=-iψ(A(I-E)).
因此,ψ限制在ME上是线性映射,ψ限制在M(I-E)上是共轭线性映射.
定理3设M和N是两个von Neumann 代数, 其中至少有一个无中心交换投影,η∈{0,±1},φ:M→N是非线性双射且满足φ(I)=I,φ(iI)*=-φ(iI), 则φ保持混合三重η-*-积当且仅当下列结论成立: i)若|η|=1, 则φ是线性*-同构;ii)若|η|≠1, 则φ是线性*-同构和共轭线性*-同构之和.
证明分两种情况进行讨论.
情形1|η|=1.
断言1φ双边保持自伴元.
取A=A*∈M, 则

所以,φ(A)=φ(A)*.由于φ-1也保持混合三重η-*-积, 如果φ(A)=φ(A)*,那么

则A=A*.
断言2φ(Z(M))=Z(N).
任取C∈Z(M)和A=A*∈M,有
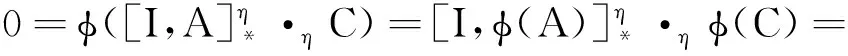
由断言1得, 对所有B=B*∈N,有Bφ(C)=φ(C)B.进一步对所有B∈N,有Bφ(C)=φ(C)B.则φ(C)∈Z(N),即φ(Z(M))⊆Z(N).类似可得φ-1(Z(N))⊆Z(M),所以,φ(Z(M))=Z(N).
断言3φ(iI)=iI.
一方面, 由φ(iI)*=-φ(iI)得
(5)
另一方面,
(6)
由式(5)和式(6)可得φ(iI)2=-I.再由式(5)得φ(ηI)=ηI.若η=i,则φ(iI)=iI.
断言4φ是线性*-同构.
任取A∈M,由
得φ(ηA)=ηφ(A).任取A,B∈M,由
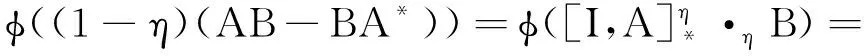
得
φ(AB-BA*)=φ(A)φ(B)-φ(B)φ(A)*.
(7)
在式(7)中取A=iI得φ(iB)=iφ(B).再由(7)式得φ((iA)(iB)-(iB)(iA)*)=φ(iA)φ(iB)-φ(iB)φ(iA)*.由此可得
φ(AB+BA*)=φ(A)φ(B)+φ(B)φ(A)*.
(8)
结合式(7)~(8)可得φ(AB)=φ(A)φ(B)和φ(BA*)=φ(B)φ(A)*.取B=I得φ(A*)=φ(A)*.类似定理2的第六步得φ是实线性,结合φ(iB)=iφ(B)得φ是线性*-同构.
情形2|η|≠1.
断言1φ保自伴幂等元.

φ(|η|2A)=|η|2φ(A).
(9)
任取A=A*∈M,由
(1-η)φ(A)+(η-|η|2)φ(A)*

断言2设i,j∈{1,2}且i≠j,则φ(Nij)=Mij.
任取Aij∈Mij,由
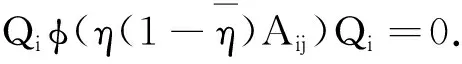
得Bji=0,所以φ(Mij)∈Nij.考虑φ-1,得φ(Mij)=Nij.
断言3φ(Mii)⊆Nii,i=1,2.
取Aii∈Mii,设i≠j,则
由此可得Qjφ(Aii)Qi=Qiφ(Aii)Qj=Qjφ(Aii)Qj=0,因此φ(Mii)⊆Nii.
断言4对所有A,B∈M,有φ(AB)=φ(A)φ(B).
为了证明φ(AB)=φ(A)φ(B),只需考虑φ(AijBkl)=φ(Aij)φ(Bkl).i、j、k、l∈{1,2}.若j≠k,由断言2和断言3得φ(AijBkl)=φ(Aij)φ(Bkl)=0.下面只需考虑j=k.
由φ(Bij)φ(Aii)*=0得
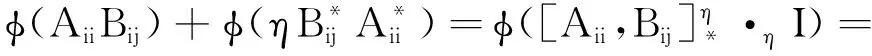
由断言2和断言3得φ(AiiBij)=φ(Aii)φ(Bij).
对所有Tij∈Nij,i≠j,由断言2得Cij=φ-1(Tij)∈Mij,则
φ(AiiBii)Tij=φ(AiiBiiCij)=φ(Aii)φ(BiiCij)=φ(Aii)φ(Bii)Tij.
由断言3和引理2得φ(AiiBii)=φ(Aii)φ(Bii).
由式(9)得

由此可得φ(AijBji)=φ(Aij)φ(Bji),φ(BjiAij)=φ(Bji)φ(Aij).
任取Tji∈Nji,i≠j,有Cji=φ-1(Tji)∈Mji,所以
φ(AijBjj)Tji=φ(AijBjjCji)=φ(Aij)φ(BjjCji)=φ(Aij)φ(Bjj)Tji.
由引理2得φ(AijBjj)=φ(Aij)φ(Bjj).
断言5φ是线性*-同构和共轭线性*-同构之和.

φ(A*)=φ(A1-iA2)=φ(A1)-φ(iA2)=φ(A1)-φ(iI)φ(A2)=φ(A1)*+φ(iI)*φ(A2)*=φ(A1)*+φ(iA2)*=φ(A1+iA2)*=φ(A)*.
即φ(A*)=φ(A)*.由断言4得φ(iI)2=φ((iI)2)=-I.类似定理2的第六步得结论.

