C3-和C4-临界连通图的结构

覃城阜，莫芬梅

(南宁师范大学 数学与统计学院，广西 南宁 530001)

1 主要结果

本文所讨论的图都是简单图。设G=(V,E)是一个图,其中V表示顶点集,E表示边集。对于W⊆V,记NG(W)={y|y∉W且y与W中的点相邻}。特别地，当W={t}时将NG({t})简记为NG(t)。与x关联的边的数目称为x的度数,记为dG(x),显然dG(x)=|NG(x)|。令Vk(G)={x∈V(G)|d(x)=k}。在不引起混淆的情况下可以省略下标G。

设G是连通图，T是V(G)的一个子集,如果G-T至少有2个分支,称T为G的点割。特别地,如果|T|=(G),则称T为G的最小点割。如果|T|=l,则称T是l-点割。设T为G的最小点割,x是T中的一个点,A是G-T的一个分支,由最小点割的定义可知N(x)∩A≠∅。

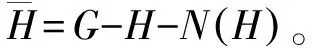
设G是连通图，如果G的每个顶点都包含在最小点割中,则称G是临界图；如果G的每条边都包含在最小点割中,则称G是一个收缩临界图。

定理1[1]如果G是C3-临界图,则κ(G)≥6；如果G是C-临界图,则κ(G)≥8。

设G为至少有k+2个顶点的k-连通图。如果对G的每条边e都有κ(G-e)<κ(G),则称G是极小k-连通图。因此，对极小k-连通图G的任意一条边e=xy,G-e有一个点割T分离x和y，且|T|=k-1。此外,G-xy-T恰好包含2个分支,且其中一个包含x,另一个包含y。若图G既是Cm-临界图，又是极小k-连通图,则称G是Cm-临界极小连通图,这里k=κ(G)。

Ando等[11]证明了以下定理2。

定理2[11]设G是C2-临界极小6-连通图,则G的每一个顶点都与一个6度点相邻。

显然,C3-临界极小6-连通图一定是C2-临界极小6-连通图。由定理2,C3-临界极小6-连通图的每一个点都与一个6度点相邻。设G6是图G中由6度点导出的子图,Poster[17]证明了如下定理3。

受文献[6]中证明方法的启发，本文对C3-临界极小6-连通图中的局部结构进行讨论，证明这类图中每个顶点都与2个6度点相邻,由此可以推出Poster的结果。

定理4设x是C3-临界极小6-连通图的一个顶点,则x与2个6度顶点相邻。

由定理4 可知，G6中每个分支的最小度为2,于是每个分支至少有1个圈,因此定理3可以作为定理4的一个推论。

基于对C3-临界极小6-连通图结构的认识，本文对C4-临界连通图的连通性进行讨论,得到如下定理5。

定理5设G是C4-临界连通图,则κ(G)≥7。

由定理1及定理5可以提出如下问题。

问题1Cm-临界连通图的连通度至少为m+3。

2 预备引理

本章给出一些引理，这些引理在主要结果的证明中将会用到。

引理1[1]设G是一个连通图,E0⊆E(G),M和M′是2个不同的E0-断片,并且U=N(M),U′=N(M′)。如果(U′∩M)∪(U′∩U)∪(U∩M′)含E0中1个元素,则下面结论成立：

③ 如果M∩M′≠∅，x∈(U′∩M)∪(U′∩U)∪(U∩M′)，且N(x)∩M∩M′=∅，则

N(M∩M′)=(U′∩M)∪(U′∩U)∪(U∩M′)。

引理3[11]设M是k-连通图G的一个断片,S⊆N(M)。如果|N(S)∩M|<|S|,则M=N(S)∩M。

引理4设G是一个连通图,a、b是G的2个顶点,使得N(a)-{b}=N(b)-{a},则a∈U当且仅当b∈U,这里U是G的一个最小点割。

类似引理4的证明，容易得到如下引理5。

引理5设G是C2-临界k-连通图,M={a,b}是G的一个断片，M′是一个az-断片,其中z∈N(M)。如果N(M)-{z}⊆N(b),则M⊆N(M′)。

引理6[18]设G是一个极小k-连通图,则G-Vk(G)是一个森林。

设G是一个极小k-连通图,C是G的一个圈，则由引理6可知V(C)∩Vk≠∅。

3 定理4的证明

引理7设G是一个C3-临界极小6-连通图,H={x,y}是G的一个断片,则以下结论成立：

①x和y中有1个6度点；

② 如果d(x)=7,则V(y)∩N(H)⊆V6(G)。

证明由H={x,y}可知d(x)≤7,d(y)≤7。假设x和y都是7度点,则N(x)=N(H)∪{y}，N(y)=N(H)∪{x}。因为G是一个极小6-连通图,所以G-xy有一个5-点割S，将x和y分离。注意到N(H)⊆NG-xy(x)∩NG-xy(y),即N(H)⊆S,这与S是5-点割矛盾。因此①成立。

下面证明②成立。由d(x)=7,可知N(H)⊆N(x)。由①可得d(y)=6。设N(H)={x1,x2,…,x6},不失一般性,设N(y)∩N(H)={x1,…,x5}。

引理8设G是一个C3-临界极小6-连通图,H是G的一个关于边ab的断片,且满足|H|≤2，则d(b)=6,或者N(a)∩V6(G)∩H≠∅。

证明如果H⊆V6(G),则由N(a)∩H≠∅可知N(a)∩V6(G)∩H≠∅，于是引理成立。故不妨设u∈H满足d(u)=7,则|H|=2。设H={u,v},由引理7可知d(v)=6。如果av∈E(G),则N(a)∩V6(G)∩H≠∅,引理成立。若av∉E(G),则vb∈E(G),由引理7可得,d(b)=6,引理成立。证毕。

证明不妨设H是满足引理条件的极小断片,如果|H|≤2,由引理8,N(a)∩V6(G)∩N(H)≠∅或者N(a)∩V6(G)∩H≠∅,引理成立。于是不妨设|H|≥3。设a1∈N(a)∩H,M是一个断片满足{a,a1}⊆N(M)。

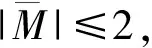
本章剩余部分将证明定理4。设u∈V(G),由定理3可知u有一个6度邻点,记为u1。令E′(u)=E(u)-{uu1}。假设N(u)∩V6(G)={u1},由引理9,下面断言1成立。

断言3存在一个E′(u)-断片H,使得u1∈N(H)。

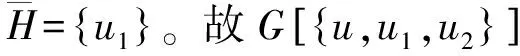
由断言3,选取一个E′(u)-断片H,使得u1∈N(H)且|H|尽可能小。设u2∈N(u)∩N(H)-{u1}，若|H|≤2,则由引理8可得d(u2)=6或者N(u)∩V6(G)∩H≠∅，此时有|N(u)∩V6(G)|≥2,矛盾。所以可设|H|≥3。设u3∈N(u)∩H。

断言4存在一个断片M,使得{u,u1,u3}⊆N(M)。

由断言4，取断片M使得{u,u1,u3}⊆N(M)，则{u,u1}⊆N(H)∩N(M)。

断言5H⊆N(M)。

下面证明定理4。

4 定理5的证明

本章先给出3个辅助引理，再给出定理5的证明。

引理10设G是C4-临界图6-连通图。若A={a，b}是一个连通断片,x∈N(A),xa∈E(G)且xa不在三边形中。令TB是包含{x,a}的最小点割，B是TB-断片。若B∩N(A)={c，d},则A⊂TB且cd∈E(G)。

先证明A⊂TB。由xa不在三边形中可知b与x不相邻，故b与TA-{x}中的每一个点都相邻，由引理5可知A⊂TB。

由断言6及对称性，不妨设B∩C=∅。

由Cm-临界连通图的定义可知下面引理12成立。

引理12设G是Cm-临界连通图，e∈E(G)是G的边，若κ(G-e)=κ(G)，则G-e也是Cm-临界连通图。

下面证明定理5。

定理5的证明设κ(G)≤6。由定理1可知κ(G)=6。由引理12,不妨设G是极小C4-临界连通图。由极小C4-临界连通图的定义可知G是极小6-连通图。若G中不存在K5,则G是C-临界连通图,由定理1可知κ(G)≥8,矛盾。故G中存在K5,设G[{x,x1,x2,x3,x4}]≅K5。注意到G是极小6-连通图,由引理6可知G中每一个圈上都有 6 度点。考虑三边形xx1x2,由对称性，不妨设x是6度点。令N(x)={x1,x2,x3,x4,x5,x6}。

断言8x5x6∉E(G)。

断言9xtxi∉E(G),这里t∈{5,6},i∈{1,2,3,4}。

证明由对称性,只证明x5x1∉E(G),其他类似可以证明。

设x5x1∈E(G),则x5x1x是三边形。取完全图Km使得{x5,x1,x}⊂Km。在满足m≤4 的前提下,使m尽可能大。取TA是包含Km的最小点割,A是TA-断片。

断言9.1A∩B=∅。

由断言9.1及断言9.2可知A⊆TB。

断言 9.3|A|=2。

由断言9.3,设A={x6,u}。由x5x6∉E(G)可知x6x1∈E(G)。此时x5与x6的位置完全对称，因此,由断言9.3,不妨设B⊆TA,B={x5,v}。

断言 9.4|TB∩TA|=2。

下面证明定理5。

断言10A1∩A2=∅。

由断言10及断言11可知A1⊆T2。注意到A1和A2是完全对称的,因此可设A2⊆T1。

断言12|A1|=|A2|=2。

由x5x6∉E(G),TC-{x5}⊆N(x6)。由引理5可知A1⊆TC。