基于改进权函数的探地雷达和无网格模拟检测混凝土结构空洞缺陷工程中的数学问题

张冠军，余 聪，黄 山，舒志乐，刘保县，吴海宽*

（1.四川建筑职业技术学院，四川德阳 618000；2.成都农业科技职业学院，四川成都 611130；3.成都工业学院，四川成都 611730；4.西华大学应急管理学院，四川成都 610039）

1 研究现状

无网格计算方法（也称为无单元方法）最早出现于1977 年。无网格方法具有计算精度高、自适应能力强和灵活性高等特点[1]，这些方法包括光滑粒子流体动力学（SPH）方法[2]、扩散单元（DE）方法[3]、无网格伽辽金（EFG）方法[4]，单位有限元（PUFE）方法[5]、h-p 云方法[6]和再生核粒子（RKP）方法[7]。

在这些无网格方法中，EFG 方法是最流行的方法之一，并在许多工程领域中使用。通过前人的工作可以发现，基于不同权函数的无网格方法应用于不同的工程领域，但很少用于探地雷达无损检测领域。因此，将基于改进法向权函数的无网格方法应用于探地雷达的无损检测。在无网格法中引入了改进的权函数。权重函数可以提高无网格方法的计算速度和精度。采用无网格法，结合电磁波理论和透射吸收边界条件，模拟了混凝土结构内部无损探地雷达探测到的损伤信号。

2 实验和模拟方法

2.1 实验和测试方法

混凝土结构空隙模型的设计示意图和制作见图1。模型由C30 混凝土制成，细骨料为砂，粗骨料由大米和石头制成。水泥标记为32.5R。水泥：砂：砾石：水的比例=300:680:1260:160（所有单位均为kg/m3）。中空形状由胶合板形成。为了确定空腔的位置，将试块分为三层进行浇注。浇筑第一层以放置空腔模型的截面，浇筑第二层以淹没空腔的中心截面，并在设计顶部浇筑第三层。浇筑后28 d 浇水和维护后，拆除模板。

图1 混凝土结构空腔模型示意及制作图（mm）

模型采用美国探地雷达SIR3000 探测，混凝土结构模型采用900 MHz 天线测量。在测线布置方面，当测线数量较大时，实际工程中测线过多会造成巨大工作量，不符合实际工程情况。当测线太少时，最终检测结果的准确性会受到影响，无法准确反映内腔疾病的真实情况。可以看出，不同距离的测量线对测试有不同的影响。因此，综合考虑，选择43 条测线分别布置在坐标的X 和Y 方向，测线之间的距离为2.5 cm。检测范围为105 cm×105 cm，在模型上精确绘制测量线，为后续检测测试做准备。测试方法使用距离模式。距离模式通过安装在天线上的固定轮的旋转来检测，以触发天线发射电磁波。在使用距离测量之前，需要校准车轮。校准后，可以精确测量车轮行驶的距离，从而有效定位目标。

2.2 改进的正态权函数

鉴于形状函数的连续性受无网格方法中权函数的连续影响，选择合适的权函数在无网格方法非常重要，可以显著提高计算速度的精度和收敛性。

权重函数表示为两点之间距离的函数，

其中ri=||x-xi||是x 和xi之前的距离

（1） 如果权函数是非奇异的，则权函数相对于坐标x，y，z 的偏导数可以通过以下方式发生，假设ωi（1）如果k 是一个正整数，则ωi有相对于x，y，z 的第次偏导数。

（2） 如果k 不是一个正整数, 但是k＞n/2，则ωi至少有n 关于x，y，z 的偏导数。

常见的标准函数如下

设t1=ρcosθ，t2=ρsinθ 则t12+t12+ρ2和ρ ∈（0，+∞），θ∈（0，2π）

则等式（4）可以写成

对数正态函数可以表示为

等式（6）是大于零的函数。

等式（7）可以通过将上述替换为

根据权函数的定义，对数正态函数可以用作权函数。设r=lnx-μ 则改进的法向权函数为

其中σ 和μ 根据正常函数定义。图2 是改进的正常权函数的示意图。可以看出，μ 在一定条件下，σ 的值尽可能小。

图2 改进的权函数曲线

一般工程应用中常用的权函数包括指数权函数、高斯权函数、三次样条权函数和正交样条权函数。函数公式如下

（1） 指数权函数

（2） 三次样条权函数

（3） 正交样条权函数

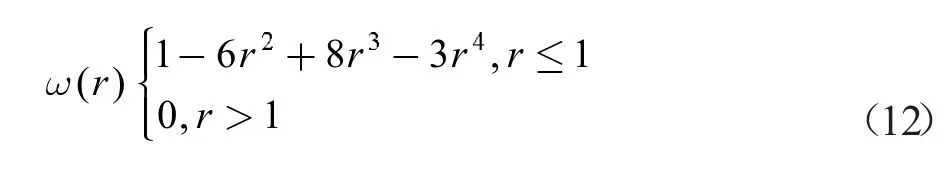
（4） 高斯权函数

3 结果和分析

3.1 探地雷达探测结果

检测结果的二维滤波图像和三维切片图像见图3和图4。

图3 探地雷达检测二维FIR 滤波图像

图4 探地雷达探测的3D 切片图像

3.2 模拟结果

数字模拟采取的空腔模型为1 m×0.5 m 的矩形，空腔为菱形。菱形腔的对角线长度为20 cm，中心点位于整个模型的中心。混凝土的相对介电常数为10，空腔中介质的相对介电常数为1，混凝土的电导率为0.005 s/m。背景网格间距为0.1 m×0.1 m，共设置100×50 个背景网格，高斯积分阶数为4。使用MATLAB 软件编制相应程序，模拟模型的无网格方法（图5）和不同时间的波场强度。

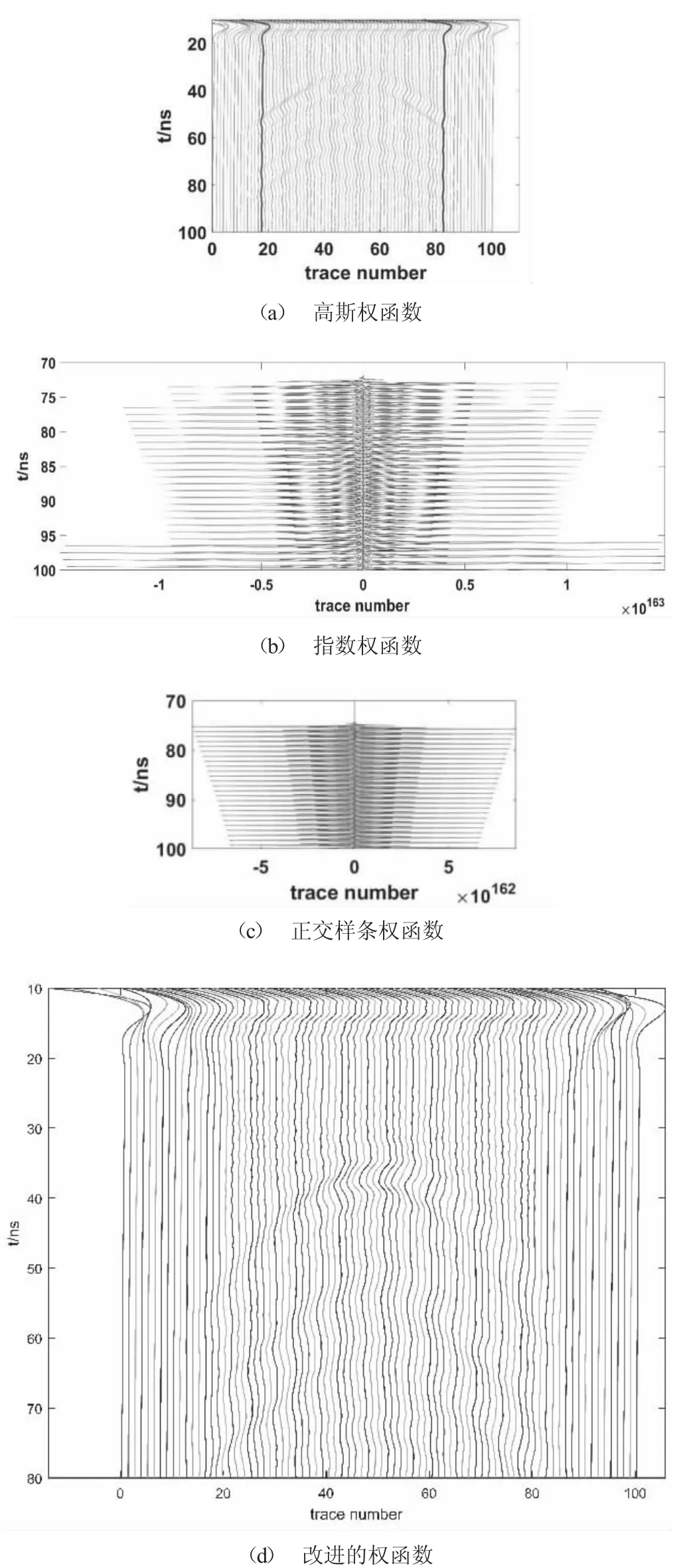
图5 数值模拟示意图

3.3 分析

在选择合适的权函数时，应考虑权函数的收敛性和准确性，并减少计算工作量。

在灵敏度方面，改进的权函数、指数权函数和高斯权函数随参数变化显著，表明它们对参数高度敏感。不同的参数选择导致不同的权重。因此，可以通过调整参数使权重函数更具适应性。三次样条函数的权函数类似于正交样条的权函数。由于三次样条的权函数和正交样条函数的权函数不包括附加参数，因此不会出现参数敏感性问题。因此，三次样条的权函数和正交样条权函数的拟合度较差。

在收敛性方面，改进的权函数、指数权函数和高斯权函数具有与参数选择相关的收敛性。随着σ 的减小，改进权函数的收敛速度加快，收敛效果良好。随着α 的增加，指数权函数和高斯权函数的收敛速度逐渐加快，收敛效果逐渐改善。然而，高斯权函数只有在α 大于1 后才逐渐显示出改进的收敛性能。三次样条和正交样条权函数的收敛性是固定的，因为没有附加参数，并且三次样条权函数的聚合性优于正交样条线权函数。

在相同CPU 和计算机的程序计算方面，每个权重函数的计算时间明显不同。其中，改进权函数、高斯权函数、指数权函数、正交样条权函数和三次样条权函数的计算时间分别为0.106 733 s、0.112 047 s、0.112 874 s、0.130 706 s 和0.114 216 s。计算时间顺序为：改进权函数<高斯权函数<指数权函数<三次样条权函数<正交样条权函数。可以看出，改进权函数排名最低，而正交样条权函数排名最高。

从收敛性、灵敏度和计算时间的分析可以发现，改进权函数比其他权函数具有一定的优势，包括灵敏度更高、收敛更明显和计算时间相对较小。因此，将改进权函数应用于无网格方法可以提高模拟的收敛性和精度，并减少计算时间。

图3 和图4 显示了探地雷达的二维和三维检测结果。2D 检测结果表明，X 方向和y 方向FIR 滤波图像。如图3 所示，不同方向的结果也不同。双曲线图像由x 方向上的检测结果表示。在y 方向上检测到黑色区域。三维检测结果表明，一定深度切片图像的探地雷达检测。混凝土结构的内部缺陷反映在图4 中水平面的白色区域中。

混凝土结构内部缺陷的无网格法模拟结果见图5。对于空腔缺陷，弧形曲线反映在图中。该弧形曲线两侧的能量较弱，因此曲线逐渐变薄。在中间，能量最强，曲线最厚。由于吸收不良，在杂波中会出现一些图形。模拟不同时间的波场强度。0-20 ns、0-40 ns、0-60 ns、0-80 ns、0-100 ns 表示电磁波场逐渐增大的规律。从模拟结果可以看出，电磁波在传输过程中波场强度明显增强，而在缺陷外部时波场强度减弱。

4 结论

通过对权函数、无网格法和实验的分析，得出以下结论。

（1） 引入了一种新的改进权函数，并证明了其适用性。在参数选择方面，μ 选择了某个值，同时σ值较小。在收敛性、精度和计算时间消耗方面，改进权函数比其他权函数具有更多的优势。

（2） 将改进权函数应用于无网格计算方法。结果表明，基于改进权函数的无网格法正演模拟与实验观测基本一致。正演模拟程序具有良好的适用性，并说明了理论分析的正确性。

（3） 波场强度的模拟结果反映了探地雷达在混凝土缺陷中电磁波传播的基本规律。当电磁波在传输过程中，波场强度明显增强，而当电磁波位于缺陷外部时波场强度减弱。